量子可逆逻辑电路综合

乐 亮, 解光军

(合肥工业大学电子科学与应用物理学院,安徽合肥 230009)

0 引 言

从20世纪60年代开始,摩尔定律在几十年的时间里都是近似成立的。然而,大多数观察家预期这将在21世纪的前20年内结束:当电子器件越做越小的时候,其内部量子效应也越来越明显,制造计算机的传统方法在进一步提高集成度上越来越显得力不从心;与此同时,集成电路能耗会导致计算机芯片发热,这一点也影响了芯片集成度的进一步提高。集成电路功耗主要来自于计算过程中的不可逆操作,例如,对于2个比特的异或操作,只有一个比特的输出。这个过程中损失了一个自由度,这正是一个不可逆操作,而损失掉的自由度就转化为热量耗散掉了。所以消除能耗的关键就是寻找可逆操作替代计算过程中的不可逆操作。量子计算就是基于量子力学而非经典物理学的思想进行的计算,量子计算中每一步操作都可以用一个幺正变换来表示,因而每一个操作都是可逆的。

量子计算机不丢失输入信息,不存在热耗散,从理论上解决了芯片的热耗问题,量子计算机可以等效为一个量子图灵机。量子图灵机是一个抽象的数学模型,理论上已证明,量子图灵机可以等价为一个量子逻辑电路。类似于经典计算机是由包含连线与逻辑门的电路构建而成,量子计算机是由包含连线和量子逻辑门级联形成、处理量子信息的量子电路建造的。如何用计算机自动综合量子电路成为研究的重点。

1 量子可逆逻辑电路概述

利用微观粒子状态表示的信息称为量子信息,量子信息的基本单位是量子比特。与经典信息不同,量子比特能够以叠加态的形式存在,任何量子比特均可由一个二元向量形式表示:|ψ〉=a|0〉+b|1〉,其中a和b为复数,满足归一化条件:|a|2+|b|2=1。在经典信息系统中,n个比特只能够代表2n个不同的状态;而在量子信息系统中,n个量子比特能够代表的不同状态的数量与这2n个态所能叠加出的态的数目是一致的。这个特点使得量子比特在其所能够表达的信息量的数量上,大大优于经典比特。

处理量子信息的基本单元是量子逻辑门。量子信息经过各个量子逻辑门时,依据门功能发生变换。量子逻辑门对量子信息的操作其实是一个幺正变换,幺正变换的一个重要特点就是这些变换都是可逆的,即每个量子逻辑门也是可逆的。主要的量子逻辑门有Toffoli门、Fredkin门等。

量子电路是由若干量子逻辑门级联构成,它是对量子信息作一系列幺正变换以实现电路功能。量子可逆逻辑电路具有以下特点:①输入线数与输出线数相等;②没有扇出与扇入;③没有反馈;④电路分层级联,有时为保证电路可逆性需要人为添加一些辅助位,即没有用的数据位。一个n位输入、n位输出的量子电路,称为n×n规模的量子电路。

可逆电路的量子代价是指它所有量子门的量子代价的总和,而量子门的量子代价是指这个门为了实现其可逆函数功能,所需要完成的基本的量子操作的量子代价的总和。不同量子门的量子代价不同。

2 量子可逆逻辑电路综合方法

经典电路的综合是用适当的电路元器件以适当的连接方式实现所需要的功能,量子电路的综合也类似于此:找寻适当的量子门级联方式实现指定功能。在量子电路可逆逻辑综合问题的研究中,不只为了找到量子电路可逆的执行方法,而且要在综合结果中尽可能找到最低的量子代价,但这并不意味着只保证综合电路的门数最少。传统的逻辑综合方法中,逻辑门的数量被看作是一个电路代价的重要因素。而从量子电路可逆逻辑综合的观点看,还存在另一个重要的事实,那就是垃圾信息输出的数量。

在使用可逆量子门进行可逆逻辑设计过程中,输入的数量与输出的数量必须是相等的。一个量子可逆逻辑电路中,可逆性要求输出门总数与输入门总数相等。所以在很多情况下,垃圾信息是不可避免的。在寻找量子逻辑电路最低代价的过程中,对于相同量子门电路的优化问题,最小化门的数量仍然是可逆逻辑优化的重要目标。以下主要以Toffoli门为例对电路综合方法作说明,仅以量子门数量作为优化衡量标准。

2.1 基于变化法的综合

由文献[1,2]提出的基于变换法的综合方法主要是通过一些变换规则,将输出值逆向逐次变换成输入值,在每一次的变换过程中选取相应的Toffoli门,最终构成所需要的量子电路。设输入为i,输出为f(i),变换的步骤如下:

(1)如果 f(0)≠0,则翻转输出 f(0)中所有为1的量子位。每一位翻转都要求用到一个1×1的Toffoli门(即NOT门)。如果将变换后的可逆函数记为f+,那么这一步最后得到的结果将满足f+(0)=0。

(2)依次考虑输入 i,其中i满足 1≤i＜2n-1。如果f+(i)=i,我们的目的达到了,就不需要对电路进行任何变换,也就不需要添加 Toffoli门;如果f+(i)≠i,那么对于这一输入i,需要添加合适的Toffoli门,对电路进行变换,以使得变换后得到的新的布尔函数 f++满足 f++(i)=i。添加的Toffoli门将满足 f+(i)→i。

对于在输入i的二进制形式中为1而在输出f+(i)的二进制形式中却为0的量子位,用在所有相应位置为1的比特序列p来表示,那么为了实现 f+(i)→i的匹配,必须在输出端与比特序列p中为1的量子位相应的位置添加1;相反,对于在输入i的二进制形式中为0而在输出 f+(i)的二进制形式中却为1的量子位,用在所有相应位置为 1的比特序列 q来表示,那么为了实现f+(i)→i的匹配,必须在输出端与比特序列中q为1的量子位相应的位置清除1。

对于比特序列p的每一位pj=1,都需要在量子电路的输出端一边使用一个 Toffoli门进行翻转,并且这个Toffoli门在所有对应于输入i的二进制形式中为1的量子位上都有其一个控制点,而它的受控位则在j线上;同样,对于比特序列q的每一位qk=1,也都需要在量子电路的输出端一边使用一个Toffoli门进行翻转,并且这个Toffoli门在所有对应于输出 f+(i)的二进制形式中为1的量子位上都有其一个控制点,而它的受控位在k线上。

对于每一输入1≤i＜2n-1,第(2)步操作都通过特定顺序的Toffoli门序列完成 f+(i)→i的映射。由于这种算法是按顺序依次考虑不同的输入i的,并且步骤(1)解决的是i=0时的情形,可以确定对于0≤j＜i,有 f+(j)→j成立。这一点的重要意义在于,在步骤(2)中新使用的Toffoli门并不会影响在前一级操作所匹配成功的布尔函数功能f+(j),其中 j＜i。即一旦将一行规则变换到正确的数值,它就固定不变而与后面行所需的变换无关。显然,最后一行规则不需要变换,因为前面2n-1个数值的位置已经是正确的。

由图3中A可知，随着酶解时间的增加，辣椒碱、辣椒二氢碱及辣椒红色素的含量先增加后降低。原因可能是，温度与酶解时间有关，酶解时间短，失活不明显，最佳温度较高；反应时间越长，最佳温度越低。由于这种关系，酶的最适温度只有在一定条件下才有意义，同时由于温度过高，会导致部分酶失活。因此，确定提取辣椒碱、辣椒二氢碱及辣椒红色素的最适酶解温度均为50 ℃。

该算法具有简单、易于实现的特点,对于给定的函数功能,此算法最终总能得出一个成功的电路。但对于任意的 M,建立的函数有可能需要(M-1)2M+1个Toffoli门。在以上规则中,所描述的通过选择Toffoli门来生成电路的算法都只是处理规则的输出边,称为后向综合法。

图1所示列举了一个3输入、3输出量子电路的后向综合法的过程,按照上述规则演示了从输出端顺次加入4个门,使输出变换到与输入一致的过程:①在输出b0加一个非门使 f(0)从010翻转成000;②f1(1)=100,要将其翻转成001,先翻转a1,由于c1=1,加入一个受控端在a1控制端在c1的受控非门;f2(1)=101,③继续翻转c2加入一个受控端在c2,控制端在a2的受控非门使得f3(1)=001;④按输入的二进制数大小的升序继续考虑 f3(2)=010无须翻转,f3(3)=111≠011,需翻转c3,由于 a3、b3=1,加入一个控制端在 a3、b3受控端在 c3的 Toffoli门使得f4(3)=011;后面的输入与输出一致,变换结束。

由于规则的可逆性,我们可以将规则翻转(从输入边加门)也可以得到一个电路,称为前向综合法,再选择2种电路中规模较小的一个。一种更简便的方法是,在规则的两边同时运用这种选择策略,以输入与输出的二进制数间的汉明距离大小决定门是加在输入边还是输出边,称为双向综合法。图2演示了同一真值表用双向综合法用3个门完成电路综合的过程:①在输入端b加一个非门使f1(0)=000;② f1(1)=001,f1(2)=010无需变换,f1(3)=110,此时考虑正向变换011与111汉明距离为1,后向变换011与110汉明距离为2,前者较小所以使用前向变换加入个受控端在c1,控制端在a1、b1的 Toffoli门交换输入 011和111使得 f2(3)=011;③f2(4)=101,前向变换和后向变换都是要将100和101交换,汉明距离都为1,无论使用哪种变换方向,加入1个受控端在a2,控制端在c2的受控非门,完成变换。

由于双向综合法在加门的过程中加入对汉明距离的判断,从两边加门,更为灵活,容易得到比较简单的电路。这种方法必然可以通过真值表生成电路,具有普遍适应性。其缺点是生成电路复杂,即便经过模板法优化也难达到最优(原因在于模板的完备性及模板匹配率的局限)。

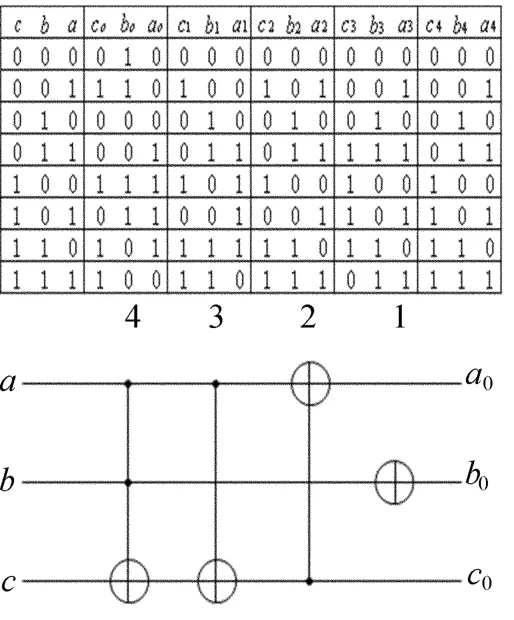
图1 后向综合法举例

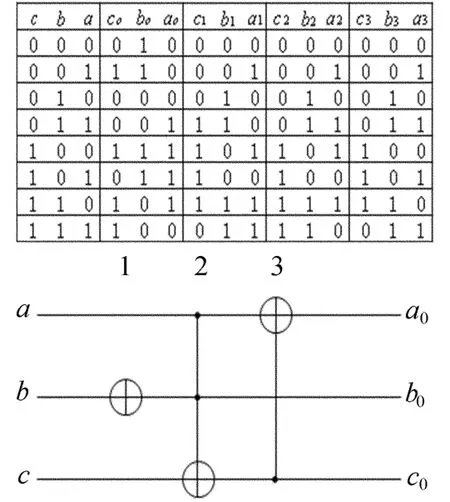
图2 双向综合法举例

2.2 穷举法

由文献[3]提出的穷举算法的核心思想是根据输入输出数,遍历所有电路,找到最优符合逻辑功能的电路。对于确定的输入、输出数n,给电路加入各种Toffoli门,门的数量由少到多,搜索到的第一个符合功能要求的就是最优电路。

此方法必定可以找到最优解,但是目前仅对输入、输出数较小的电路有可行性,随着n的增大计算量迅速增大,算法太慢,失去可行性。

2.3 RM展开式综合法

对于每一个输出Fi,有Fi=d0⊕d1P1⊕…⊕diPi,其中的d值由以下算法给出:

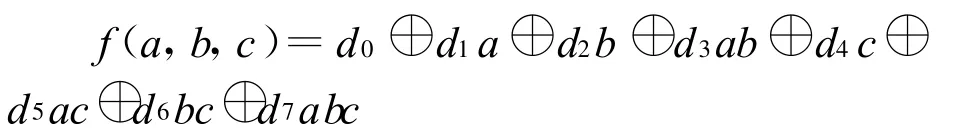
将电路功能表示成RM展开式后,就可以利用它进行量子电路综合。依据各个量子位输出量的RM表达式,找出其展开项中不含相应输入量的因子,然后依次试探量子门Toffoli(ck,xk),把原来的表达式中的 xk用代换(此代换表示所加量子门的功能),并化简,不断重复此过程,直至RM 展开式变为恒等式,即对于任意i∈{1,2,…,n},有yi=xi,将化简过程中使用的量子逻辑门顺序排列,即可生成所求量子可逆逻辑电路。

将图2的真值表生成可逆逻辑电路的过程如图3所示。

图3 RM展开式法举例

将化简过程中用到的Toffoli门,从输出到输入按顺序排列,就得到图2所示电路。代换化简的路径不止一种,通常通过优先权公式决定,也有人提出遍历所有路径,第一个完成化简的就是最优解。这种方法缺乏通用性,而且生成电路通常不是最优,只是局部最优。

2.4 基于群论的综合法

文献[4,5]将可逆逻辑电路综合抽象为群论问题,设计出基于群论GAP软件的量子电路综合算法,其性能大幅度提高。一个n×n的量子可逆逻辑门的输入和输出对可有2n!种组合,若将每个组合对应一个置换,则这些置换的集合就组成一个置换群Sn,而n阶的各种门对应的置换也在Sn中。此方法的核心思想是将目标函数所对应的置换用置换群中一些门(这些门的集合是此算法的库)的置换分解替代,并找到最简的替代组合,综合出电路。对于库L,其元素可以构成的所有置换功能的集合记做G(L)。对于G(L)中的元素a,若用L中至少minl(a)个元素串接能构成a,则minl(a)称为a在G(L)中的最小长度。以下用2个程序说明此方法的基本流程:

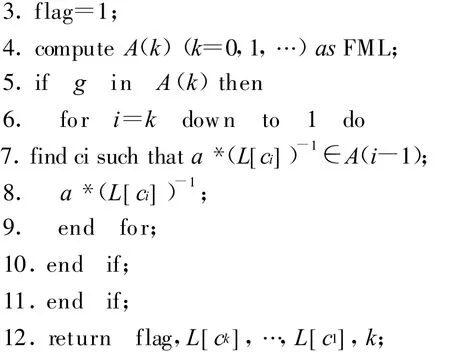
程序FML计算最小长度,将被MLR调用。

程序MLR是对于目标函数对应的置换g,用库L去求其最小长度并得出最简电路。前几步先判定g是否能由L生成,若能则定位其最小长度电路的长度k。接下来寻找L中元素ci其逆置换与g相乘后能得到最小长度为k-1的置换,如此递归下去保证每加入1个元素都使置换的最小长度减1,直到最小长度为0。

将这些元素所对应的门顺次排列起来就得到最简电路。综合3阶电路时可以用3个非门,6个受控非门,3个标准 Toffoli门构成完备的库L;对于更高阶电路,使用通用库是非常困难的,库中元素数目的变化同时影响计算速度和库的通用性,并且此消彼长。

3 结束语

量子可逆逻辑综合是一个新兴的研究领域。可逆逻辑电路的综合与优化由同一过程完成是今后研究的主流。在综合量子电路的同时还要考虑电路门的最小化和量子代价最小化,这对算法模型、算法解空间上的搜索复杂程度都有相当的考验。穷举法虽然必能找最优解但是计算复杂度太高,只能适用低阶电路;真值表变换法基于电路变换规则直接对真值表操作,对任何电路都有解,且计算复杂度低,具有普遍适用性,缺点是结果不是最优解,优化难度高;RM展开式法将电路综合过程转化为展开式化简过程,计算复杂度低,只与电路阶数n线性相关,即使遍历所有化简路径也只与m×n有关(m为最大路径数),且能找到较优解,缺点是结果不一定是最优解,有些情况下可能无解;群论法将电路用置换对的数学模型代替,合理利用群论的高性能计算,必能找到最优解,缺点是计算复杂度与2n!相关[6-9]。

在掌握和比较分析现有方法的基础上,应该继续探索新的方法,新方法应对任何目标函数都能适用,最好能确定最优解;综合模型容易转换实现,算法要能适应高阶电路,复杂程度、计算量不能随阶数增大成指数增长,可适用于高阶电路。

[1] Dueck G W,Maslov D,Miller D M.Transformation-based synthesis of networks of T offoli/Fredkin Gates[C]//IEEE CCECE,2003:211-214.

[2] Miller D M,Maslov D,Dueck G W.A transformation based algorithm for reversible logic sy nthesis[C]//DAC,2003:318-323.

[3] Shende V V,Bullock S S,M arkov I L.Synthesis of quantum logic circuits[J].IEEE T ransactions on Computer-Aided Design of Integrated Circuits and Systems,2006,25(6):1000-1010.

[4] Yang G W,Song X Y,Hung W N,et al.Group theory based synthesis of binary reversible circuits[C]//TAMC,2006:365-374.

[5] Yang G W,Song X Y,Hung W N,et al.Fast synthesis of exact minimal reversible circuits using group theory[C]//ASP-DAC,2005:1002-1005.

[6] Gupta P,Agrawal A,Jha N K.An algorithm for synthesis of reversible logic circuits[J].IEEE Transactions on Computer-Aided Design of Integ rater Circuits and Sy stems,2006,25(11):2317-2330.

[7] Wille R,G rope D.Fast exact Toffoli network sy nthesis of reversible logic[C]//ICCAD,2007:60-64.

[8] Li Z Q,Chen H W,Xu B W,et al.Fast algorithm for 4-qubit reversible logic circuits synthesis[C]//CEC,2008:2202-2207.

[9] Li Z Q,Chen H W,Xu B W,et al.An algorithm for synthesis of optimal 3-qubit reversible circuits based on bit operation[C]//WGEC,2008:455-458.