Z+Z智能教育平台在高中数学算法教学中的应用
2010-10-25张秀琦张晓燕
张秀琦,张晓燕
(1渤海大学 教育学院,辽宁 锦州 121000;2河南省实验中学,河南 郑州 450002)
Z+Z智能教育平台在高中数学算法教学中的应用
1张秀琦,2张晓燕
(1渤海大学 教育学院,辽宁 锦州 121000;2河南省实验中学,河南 郑州 450002)
在新课程标准中,算法已被列为高中数学的必修内容。本文对人教版高一数学必修3中算法章节部分进行了研究,对部分算法的效率进行了深入分析,并在Z+Z智能教育平台上对改进后的算法进行了验证。
Z+Z智能教育平台;高中数学;算法
在普通高中数学课程标准中,算法模块中要求学生通过模仿、操作、探索,学习设计程序框图表达解决问题的过程;体会算法的基本思想以及算法的重要性和有效性,发展有条理的思考与表达的能力,提高逻辑思维能力[1]。
一、人教版高一数学必修3中两个算法效率的分析
1.判断质数算法
在1-1-1节中,教材中设计了一个算法,用来判断一个数是否为质数。根据质数的定义:只能被1和自身整除的大于1的整数叫质数(教材第3页附注),学生很容易接受书中提供的算法,即设这个数为n,用2~n-1这样的数依次去除n,如果这些数都不能把n整除,则n为质数;否则n不是质数。
这个算法对于一般的数据都可以处理,而且现在计算机的速度非常快,计算的时间基本上可以忽略;但是在某些特定的问题中,等待我们去验证的数往往比较大,在这种情况下,此算法的效率就要大打折扣了。以1011107例,若要验证其是否质数,需用2~1011106去试,这样判断进行了100多万次,按此算法编写程序在QBASIC上从运行到出结果,明显感觉有时间延迟。
其实在验证的过程中,范围可以缩小,由原来的[2,n-1]改为这个证明很容易:设p为n的一个因子,即p/n为整数,记为q,如果则一定有p∈[2,也就是说,如果在中不存在n的因子,那么在也不可能有 n的因子;故只需验证这个范围即可。
这样的话,数1011107是否为质数,只需验证大约1000多次即可,效率大大提高。
2.进制转换算法
在1-3节的例4中,要求设计一个算法,把k进制数a(共有n位)化为十进制数b。其中算法第三步为:b=b+ai* ki-1,i=i+1。
在循环进行的n次中,每一次都要求一个ki-1,如果n比较小,这样做无可厚非,但人们总是忍不住追求高效率,况且对于这个问题,提高效率并不难,只需稍稍改动一下算法,在算法中设w,用来表示ki-1,显然,w每处理一位就要增长为w*k,修改后的算法如下:
第一步,输入a,k和n的值;第二步,将b的值初始化为0,i的值初始化为1,w的值初始化为1,即k0;第三步,b=b+ai*w,i=i+1,w=w*k;第四步,判断i>n是否成立,若是则执行第五步;否则返回第三步;第五步,输出b的值。
如果想进一步优化这个算法,还可以取消i,事实证明本算法中的i是完全可以省略掉的。亦可进一步延伸,让学生比较针对同一问题所设计的不同算法的区别并体验它,不但可以加深学生对算法设计重要性的认识,还可以让学生对数学知识在算法设计中的灵活应用印象深刻。
二、Z+Z智能教育平台下算法的验证
由张景中院士主持开发的“Z+Z 智能教育平台”适应我国数学课程改革的特点,充分发挥了信息技术条件下教学的优势,可建立一个让学生进行观察、实验、猜想、验证的数学学习环境,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程[2]。该软件可用于平面几何、代数、解析几何、立体几何、概率统计、算法与编程、函数等中学数学课程的教学和学习。
学习算法,关键在于编写出让计算机执行的程序。看到计算机执行自己的程序并快速准确地给出问题的解答,会让学生体会到学习算法的成就感;另一方面,若执行程序未得到自己预期的答案,则可以对自己的算法和程序进行检查,通过实践中的问题学习算法可以加深对算法及程序的认识和理解[3]。
人教版高一数学必修3中提供的算法程序是用BASIC语言编写的,教师讲授时大多在 QBASIC下运行程序,因此会出现上面提到的种种问题。相对于很多计算机高级程序设计语言来说,利用Z+Z智能教育平台的程序工作区执行程序具有无须编译直接执行命令并且即时得到运算结果的优点,也无须嵌入头文件、各种类文件即可进行对应的运算,程序执行的速度较 QBASIC下快出很多,因此更适合在数学课上使用。以下给出改进后的两个算法在Z+Z智能教育平台下的程序及运行结果。其中图1判断质数程序执行后给出结果:1011107是质数,此改进后的算法在判断1011107是否为质数时在该平台下运行较改进前无时间延迟;图 2进制转换程序执行后给出二进制数 101转换为十进制数为5。
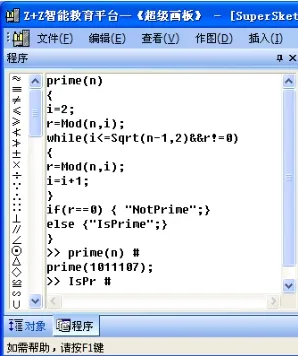
图1 Z+Z下的判断质数程序

图2 Z+Z下的进制转换程序
三、总结
本文对人教版高一数学必修 3中算法章节部分进行了研究,对算法的效率进行了深入分析,给出了在Z+Z智能教育平台上实现算法的程序,希望教师和学生能利用 Z+Z智能教育平台丰富的功能提高对数学算法的认识和理解。
[1] 数学课程标准研制组.普通高中数学课程标准(实验稿)[M].北京师范大学出版社,2000.
[2] 张秀琦,唐吉洪,刘东芝.基于Z+Z智能教育平台促进中学生数学知识建构与理解的研究[J].湖北广播电视大学学报,2010,(1).
[3] 张景中.超级画板自由行[M].科学出版社,2006.
G434
A
1008-7427(2010)09-0146-01
2010-07-19
辽宁省教育科学“十一五”规划2009年度一般课题《Z+Z 智能教育平台在农村中学教学的应用研究》(课题编号JG09CB099)的研究成果。
作者张秀琦系渤海大学教育学院讲师。
