基于RBF神经网络的商业银行客户信用评级

毛义华，刘 悦

（浙江大学 土木工程管理研究所，杭州 310027）

0 引言

随着金融业的发展，我国各商业银行已逐步建立起了企业信用风险评级系统。但因信用评级标准不一、结果不同，导致评级效率低下，存在评级对象和范围较窄的现象。由于其主要使用法人客户授信制度进行信用风险评级，对单一法人客户或集团性客户核定综合授信额度，并在额度内办理授信业务，集中控制客户信用风险的信贷管理制度，并且其授信额度理论值的测算采取“打分卡测评法”，即线性加权计算，指标和权重的确定带有很大的主观性，无法模拟企业实际信用与评测指标之间的复杂非线性关系。

规范企业信用评级管理，建立一个权威的信用等级标准评估体系，已经成为政府和社会的一种共识。因此，本文提出基于RBF神经网络的商业银行客户信用风险评级方法。试用RBF神经网络这个“特征提取器”，从大量过去的商业银行客户信用等级评定资料中自动提取各信用评价指标与企业实际信用等级之间的规律，用其超强的非线性映射能力进行仿真模拟，解决传统客户信用评价方法的不足之处。

1 客户信用评级模型构建

1.1 RBF神经网络基本思想

RBF神经网络是一个只有一个隐含层的三层前馈神经网络结构。与其他类型神经网络不同，RBF神经网络的隐层转换函数是局部响应的高斯函数，而非全局相应函数。

1.2 评价指标选取

输入层为N个单元，隐层P个单元，输出层为P个单元的RBF神经网络的数学表达为：

RBF网络是一种性能良好的前向网络。它不仅具有高速的运算能力，超强的适应能力，自组织、自学习和优秀的容错能力，而且具有全局逼近性质,等达到最佳逼近性能。与在经济管理领域常用的BP神经网络相比，RBF网络解决了其局部最优、训练速度慢、效率低等问题。这些优势使得RBF与传统的预测、决策、规划、调度等方法相比，显示了其在处理高度非线性问题中的独特魅力。

指标的选取是极为关键的一步，指标选择的好坏直接影响结果的准确性。网络的输入神经元选取与客户企业信用相关的指标，直接用企业信用等级作为网络的输出神经元。

客户企业的盈利能力、经营能力、偿债能力均与企业信用息息相关。因此，本文选取销售收入现金实现率、销售净利润、主营业务收入、利润净额这几个指标全面的反应客户企业的盈利能力；选取总资产周转率、应收账款周转率这两个指标来反映客户企业的经营能力；用流动比率、资产负债率来评价其偿债能力。此外，本文亦将现金流量利息保障倍数、营运资本资产比率、总资产报酬率、资产总计、负债总计这几个指标作为输入变量，以全面地反映贷款企业的财务综合实力。

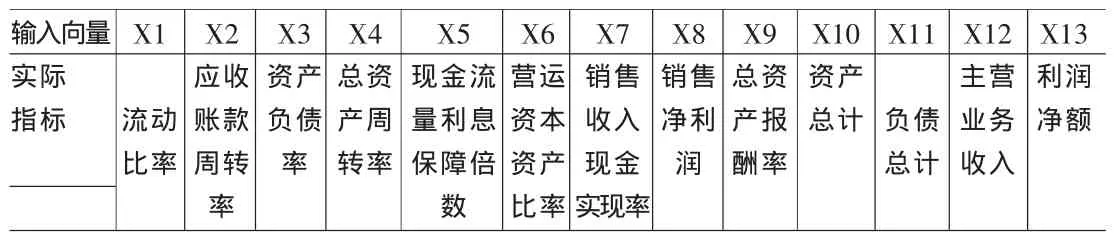
表1 输入向量表

表2 输出向量取值表

根据上述分析，本文选取流动比率、应收账款周转率、资产负债率、总资产周转率、现金流量利息保障倍数、营运资本资产比率、销售收入现金实现率、销售净利润率、总资产报酬率、资产总计、负债总计、主营业务收入、利润净额这13个指标作为输入向量。选取信用等级这一个指标作为输出向量。信用等级的5个类别分别对应与输出变量Y的5种取值，即 AAA级，AA级，A级，B级，D级。

1.3 数据无量纲化处理

本文从A银行取得了339家匿名客户企业的财务及信用信息作为神经网络的训练和测试样本，并对收集的有效样本按以下方式进行无量纲化处理：

(1)效益型指标，如应收账款周转率、总资产周转率、现金流量利息保障倍数、营运资本资产比率、销售收入现金实现率、销售净利润、总资产报酬率、资产总计、主营业务收入、利润净额，其指标值越大越好，故按公式（1）进行无量纲化，：

(2)成本型指标，如资产负债率、负债总计，其指标值越小越好，故按公式（2）进行无量纲化：

(3)区间型指标，如流动比率，其指标值落入某区间最好，故按公式（3）进行无量纲化：

其中，ai为第j项指标的最大值；bj为第j项指标的最小值。参考相关文献，本文认为流动比率在区间[2,4]之间最佳，故 q1=2，q2=4。

把无量纲化处理好的样本数据分为两部分：随机选取其中294家作为训练样本，45家作为测试样本。其中训练样本中AAA 级企业63家，AA级企业66家，A级企业81家，B级企业43家，D级企业41家。测试样本中AAA级企业5家，AA级企业10家，A级企业20家，B级企业7家，D级企业3家。

无量纲化后训练样本数据如表3。

1.4 网络参数选取

隐含层神经元数量的确定是神经网络的关键问题。在RBF网络训练中，传统的做法是隐含层神经元个数与输入神经元个数相等。本文采用试算法选取隐含层神经元个数，即：从零个神经元开始训练，通过检查输出误差使网络自动增加神经元。每次循环使用，使网络产生的最大误差所对应的输入向量作为权值向量w1i，产生一个新的隐含层神经元，然后检查新网络的误差。不断重复此过程直到达到误差要求或最大隐含层神经元数为止。

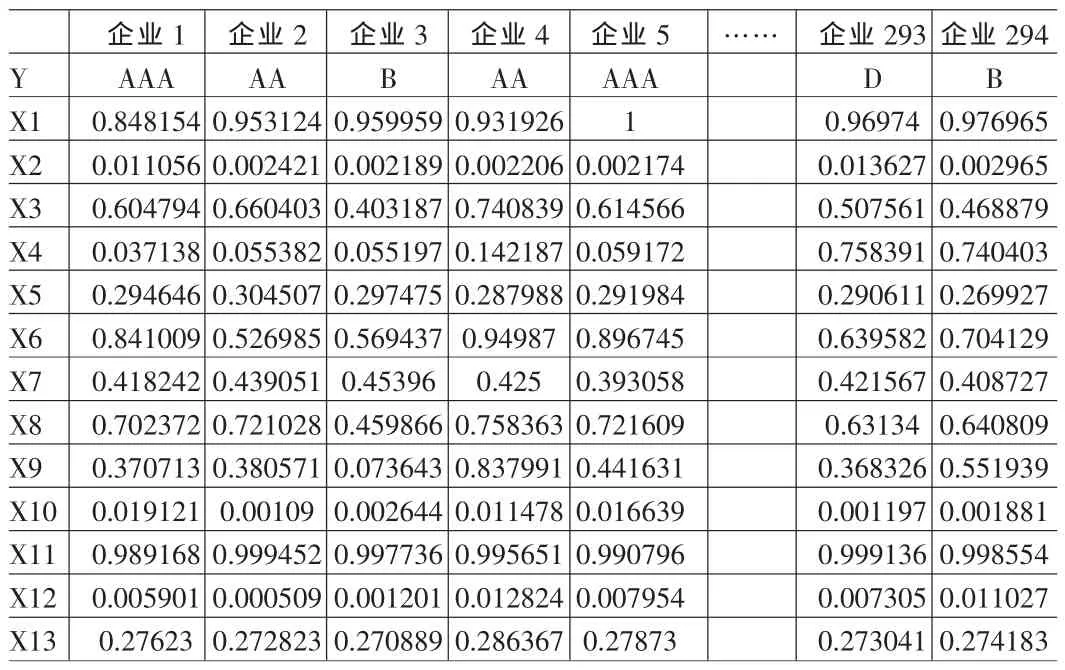
表3 训练样本数据（无量纲化后）

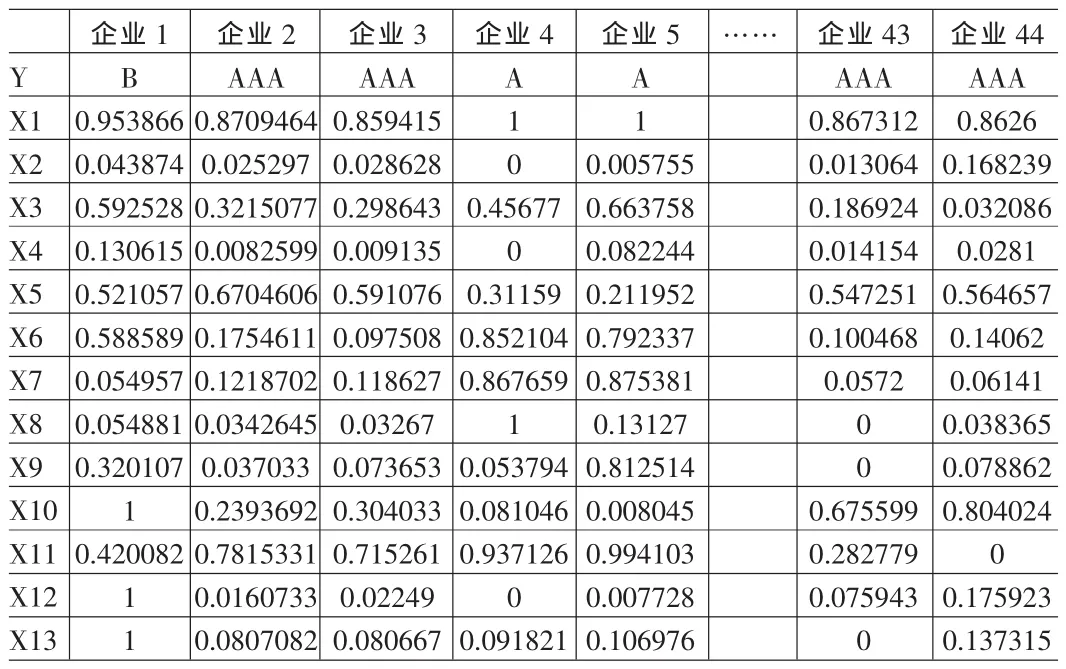
表4 测试样本数据（无量纲化后）

在RBF网络设计中，径向基函数的分布密度（spread）的确定亦十分重要。径向基函数分布密度越大，函数越平滑。一般情况，spread取1.0。本文径向基函数分布密度的取值亦采取试算法（详见表4）。当spread增大时，网络输出越接近真实值。然而，当spread取值超过某些值时，网络输出的误差反而变大。误差越小，该神经网络越精确，然而误差过小会使得神经网络训练过熟，使得网络的外推效果不好。

本文使用matlab编程，建立RBF网络。其输入层神经元个数为13，输出神经元个数为1。为使网络收敛效果好，本文采用试算法选取隐含层神经元个数：从零个神经元开始训练，逐个增加隐含层神经元个数，最终确定隐含层神经元个数。经反复试验并综合考虑隐含层神经元个数及误差，最终确定径向基函数分布密度Spread取值1.8，隐含层神经元个数为293的网络结构。

1.5 RBF网络训练

RBF网络的建立过程即训练过程，该神经网络的SSE误差为3.60486e-007，完全能达到误差要求。

1.6 RBF网络测试

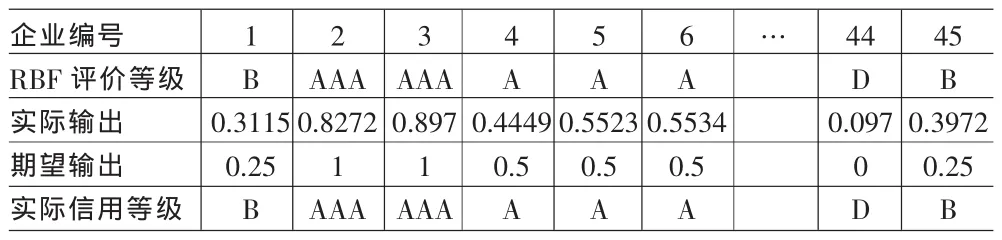
表5 测试结果对比表

训练好网络，将用45组测试样本的数据对网络进行效果测试。（测试样本数据如表4），把测试样本的输入向量输入训练好的RBF神经网络，测试结果见表5。由表5可知，用训练样本之外的45组测试样本数据测试网络，所得相对误差都较小，根据RBF网络评价的信用等级与实际企业信用等级一致，说明本信用评级模型的推广应用能力强。

2 实例分析

本文选取了企业A做实例分析。

从企业A的财务报表中，可直接得到资产总计、负债总计、主营业务收入、利润净额值分别为22078225元、15448488元、125591276.4元、146970.7元；通过财务报表其他值计算出企业A的流动比率为0.342659，应收账款周转率为138.5369，资产负债率为0.699716，总资产周转率为5.688468，现金流量利息保障倍数1.658709，营运资本资产比率-0.43409，销售收入现金实现率1.007341，销售净利润率0.00117023，总资产报酬率为0.013132。

对上述数据进行无量纲化处理，对应于输入向量（0.86632，0.347775，0.41244，0.246224，0.545231，0.200759，0.05312，0.030124，0.057492，0.18765，0.84849，0.360132，0.094923）。

经训练好的RBF网络仿真，其输出值为0.5757。因此，该公司的应属于信用等级为A级的企业。

3 结语

由于RBF神经网络能不断接受新样本、新经验并不断调整模型,自适应能力强,有超强的非线性映射功能。与常用的BP网络相比，RBF网络还解决了其局部最优值、收敛速度慢等缺点。

因此，本文用RBF神经网络从大量过去的商业银行客户信用等级评定资料中自动提取各信用评价指标与企业实际信用等级的规律，建立基于RBF神经网络的商业银行客户信用评级体系。结果表明,RBF神经网络可以精确的模拟出信用评价指标与企业实际信用之间的复杂非线性关系，解决传统评级方法中权重确定不客观、定量分析不足、评级效率低下等缺陷，形成了一套更为科学、有效和实用的信用评级方法，开拓了商业银行贷款客户信用管理工作的新视野。

[1]王春峰,万海晖,张维.基于神经网络技术的商业银行信用风险评估[J].系统工程理论与实践，1999，(9).

[2]程建.客户信用评级体系的校准度检验研究[J].山西财经大学学报，2008，(8).

[3]蒋树宽.银企信用风险管理[M].广州:广东经济出版社,2001.

[4]Touretzky,G Hinton,T Sejnowski(Eds.).Carnegie Mellon University[M].Morgan Kaufmann Publishers,1988.

[5]吴微.神经网络计算[M].北京：高等教育出版社，2003.

[6]王旭东，邵惠鹤.RBF神经网络理论及其在控制中的应用[J].信息与控制，1997，(8).

[7]杜栋，庞庆华.现代综合评价方法与案例精选[M].北京：清华大学出版社，2005.