未决赔款准备金估计的Munich链梯法及其优化
2010-10-21张连增
陈 晓,张连增
(南开大学 经济学院风险管理与保险学系,天津 300071)
0 引言
未决赔款准备金是非寿险公司财务报表上的一项最为重要的负债项目。提高未决赔款准备金评估的准确性,对于分析、评估和防范非寿险业务的财务风险,保证公司的偿付能力,以及保护被保险人的利益而言都具有重要的意义。在非寿险领域准备金评估的过程中,链梯法 (chain-ladder method)由于其简易性和几乎不需要任何假设的特点,成为基于流量三角形对未决赔款准备金进行预测的常用方法。通常,链梯法可分别应用于已决赔款(paid-loss)和已发生赔款(incurred-loss)数据。由于这两种方法都用于预测最终赔款额,我们自然期望通过这两种方法能够得到相近的预测结果。但是在实际问题中结论并非如此,依据这两类数据得到的最终赔款额有较大差异。Halliwell[1]首次从随机过程的角度研究了这个问题。之后,Quarg和Mack[2]引入Munich chainladder(MCL)模型,该模型降低了链梯法基于已决赔款数据和已发生赔款数据预测最终赔款额之间的差异,从而更加准确地估计未决赔款准备金。
本文拟运用统计学中的稳健回归 (Huber M估计法和Bisquare M估计法)和耐抗回归(LTS估计法)方法优化Munich链梯法,通过降低离群点对参数估计的干扰,进一步降低基于已决赔款数据和已发生赔款数据预测的最终赔款额之间的差异,从而更准确提取未决赔款准备金。应用软件 R-2.8.1编写程序实现链梯法、Munich链梯法和优化的Munich链梯法,并以Quarg和Mack(2004)中的数据为例,比较上述方法在未决赔款准备金评估方面的优劣。
在本文中,以 Pi,t,Ii,t(i,t=1,2,…,n)分别表示在事故年 i、发展年t年末的累计已决赔款和累计已发生赔款。以表示事故年在准备金评估日(假设为年末)的当前发展年,那么Pi,t,Ii,t(1≤t≤ci)为已知数据,Pi,t,Ii,t(ci<t≤n)为预测值。
1 链梯法及其缺陷
链梯法假设如果没有外来因素(如通货膨胀等)的影响,那么各事故年的赔案在未来各发展年的赔款进展是平稳的。这个假设表现在流量三角形中就是:平均而言各列的数据成比例。

由链梯法定义,对于s≥ci,预测值Pi,s+1和Ii,s+1分别为:

由链梯法,依据已决赔款和已发生赔款数据计算的最终赔款额Pi,n和Ii,n分别为:
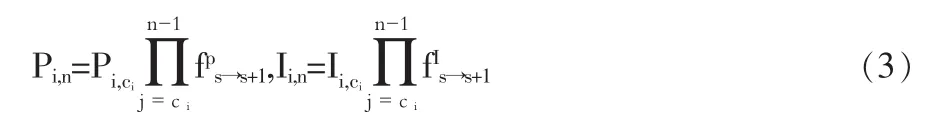
事故年i在发展年t的已决赔款额与已发生赔款额的比率定义为

所有的事故年在发展年的平均比率定义为

其中对于 ci<t≤n,Pi,t和 Ii,t为由式(2)得到的预测值。 那么对于 t≥ci,下式成立:

式(4)的详细推导见 Quarg和 Mack (2004)。 式(4)表明在各个发展年度,每一事故年P/I的预测值与所有事故年的P/I的平均值之比是常数,它为在当前发展年的对应的比值。也就是说,对于任一事故年i,如果在准备金评估日(即发展年ci年末),该比值大于1,那么在发展年n年末时,该比值也大于1;反之亦然。在递推过程中对于t≥ci,由式(4)可得:

考虑到实际意义,可以预期随着发展年t的增大,(P/I)t以递增的方式趋近于1。在准备金评估日,如果事故年i的(4)式比值大于 1,那么(5)式左边(P/I)i,t-(P/I)t为关于 t的增函数。也就是说,链梯法会把这种趋势在每一步递推中逐步扩大。具体地说,以Quarg和Mack(2004)中的已决赔款流量三角形和已发生赔款流量三角形数据(事故年为7年,发展年为7年)为例,应用链梯法计算得到各事故年在每一发展年的(P/I)比率。以发展年作为横坐标,以各发展年对应的所有事故年的(P/I)比率作为纵坐标,可以直观地发现各事故年的(P/I)比率随着发展年的增加呈现发散趋势,而非集中于平均(P/I)比率。为了直观表现这一趋势,在图1中以平滑直线连接7个发展年的平均(P/I)比率。这样导致的问题就是:对于较近的事故年,由于需要递推计算的次数较多,在最终发展年(P/I)比率距1有较大差异。由于链梯法预测最终赔款额存在上述缺陷,为此引入Munich链梯法。

2 Munich chain-ladder模型
Quarg和Mack(2004)提出Munich链梯法,成功地降低了链梯法基于已决赔款数据和已发生赔款数据得到的最终赔款额之间的差异。Munich链梯法通过P/I比率(累计已决赔款/累计已发生赔款)反映已决赔款数据P和已发生赔款数据I的相关性。
记事故年i、发展年j年末的P/I比率为(i,j=1,2,…,n):

记发展年j的平均P/I比率为:

其中 Pi,t,Ii,t(ci<t≤n)为根据式(2)得到的预测值。
Munich链梯法(简称MCL方法)通过调整发展因子来减小依据已决赔款数据和已发生赔款分别得到的最终赔款额之间的差异,其基本思想是:对于某一事故年,如果在准备金当前评估日P/I比率比较低 (低于在准备金评估日的平均P/I比率),那就意味着与其它事故年相比,该事故年截至准备金评估日已决赔款偏少或已发生未决赔款准备金偏多,因此在未来阶段赔款额会增加,从而应该增加与当前评估日相对应的发展年的已决赔款的发展因子,而减小已发生赔款的发展因子。反之,如果在准备金评估日P/I比率比较高(高于在准备金评估日的平均P/I比率),那么该事故年的已决赔款的预测值应降低,已发生赔款的预测值应升高。
记Pi(s)={Pi,1,…,Pi,s}和Ii(s)={Ii,1,…,Ii,s}分别表示事故年的已决赔款额和已发生赔款额在发展年s之前的数据。首先将所有发展年的数据标准化,得到残差值,期望为0,标准差为1。残差通过条件期望定义如下:

其中X为随机变量,而C表示某条件。
依据MCL方法的基本思想,根据以下回归模型调整发展因子。
针对已决赔款数据:

针对已发生赔款数据:
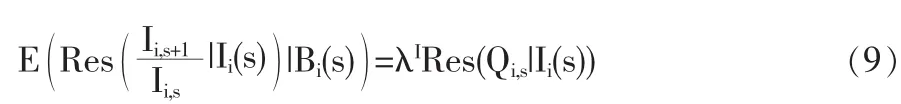
其中 λp和 λI均为常数(有关计算见下文),而且 λp,λI≥0,它们表示在残差图中的回归线斜率。Bi(s)表示二维过程(Pi(s),Ii(s))。 Q 由(6)式定义。
由残差定义,式(8)和(9)分别等价于式(10)和(11):


3 Munich chain-ladder模型的参数优化
Quarg和 Mack(2004)首次提出MCL方法时,应用最小二乘法(OLS)分别估计式(8)和式(9)中回归系数 λP和 λI,即

但是在残差图中通常会出现离群点,此时应用最小二乘法估计回归线的斜率(见式(8)和式(9))会产生较大误差,从而导致回归模型(见式(10)和式(11))不稳定。 Verdier和Klinger(2005)指出式(8)和式(9)中斜率应根据不同的发展阶段而进行相应调整。
以下应用统计学中稳健估计模型,很好地解决了应用最小二乘法求回归直线时,可能存在的某些离群点对回归的显著性(拟合度)的影响。我们将通过稳健回归(Robust regres⁃sion)和耐抗回归(Resistant regression)计算出回归线斜率,其中稳健回归方法通过降低离群点的权重增强回归的稳健性,而耐抗回归方法通过建立约束模型在回归过程中直接除去离群点。对于稳健回归方法,我们分别采用Huber M估计法(Huber’s M estimator)和 Bisquare M 估计法(Bisquare’s M estimator)设置离群点的权重[4]。
Huber M估计法:设定转折参数,权重给出如下

Bisquare M估计法 设定转折参数c=4.685,权重w给出如下:
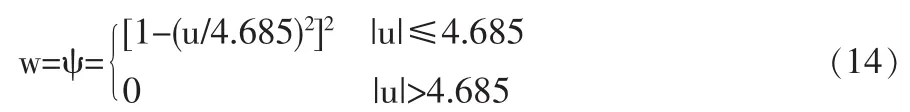
其中在式(13)和(14)中u表示采用绝对离差的中位数(Median Absolute Deviation)估计方法规范化后的残差,即
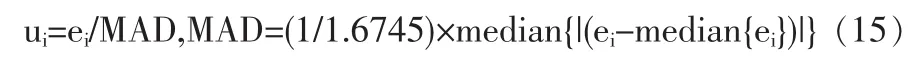
在耐抗回归方法中,我们采用LTS(Least trimmed squares)估计法除去离群点。定义

下面以Quarg和Mack(2004)中的累计已决赔款流量三角形(表1)和累计已发生赔款流量三角形(表2)数据为例,应用软件 R-2.8.1分别计算稳健回归和耐抗回归模型中的参数估计值和最终P/I(已决赔款额/已发生赔款额)比率,并将计算结果与传统CL方法和MCL方法进行比较(程序略)。
表3给出根据已决赔款数据分别用传统链梯法(CL)、Munich链梯法(MCL)和优化的Munich链梯法(MCL-Robust&Resistant Regression)预测的最终赔款额,表4给出根据已发生赔款数据用上述方法预测的最终赔款额Ii,n。由MCL方法预测得到的累计已决赔款和累计已发生赔款的数据略。
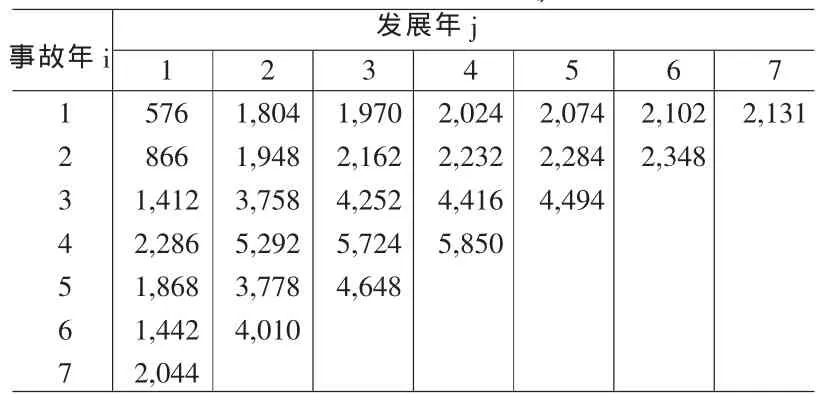
表1 累计已决赔款流量三角形Pi,j

表2 累计已发生赔款流量三角形Ii,j

表3 根据已决赔款数据预测的最终赔款额Pi,n

表4 根据已发生赔款数据预测的最终赔款额Ii,n
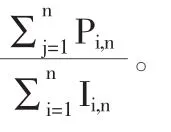
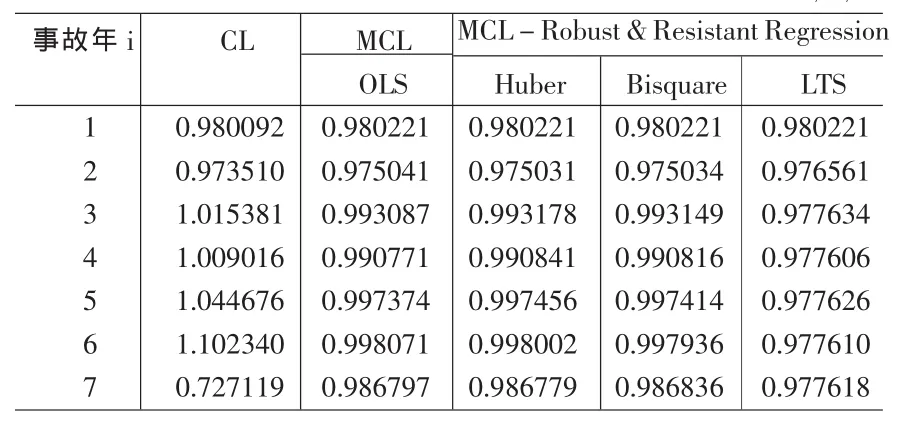
表5 已决赔款和已发生赔款数据预测的最终赔款额的比率Pi,n/Ii,n
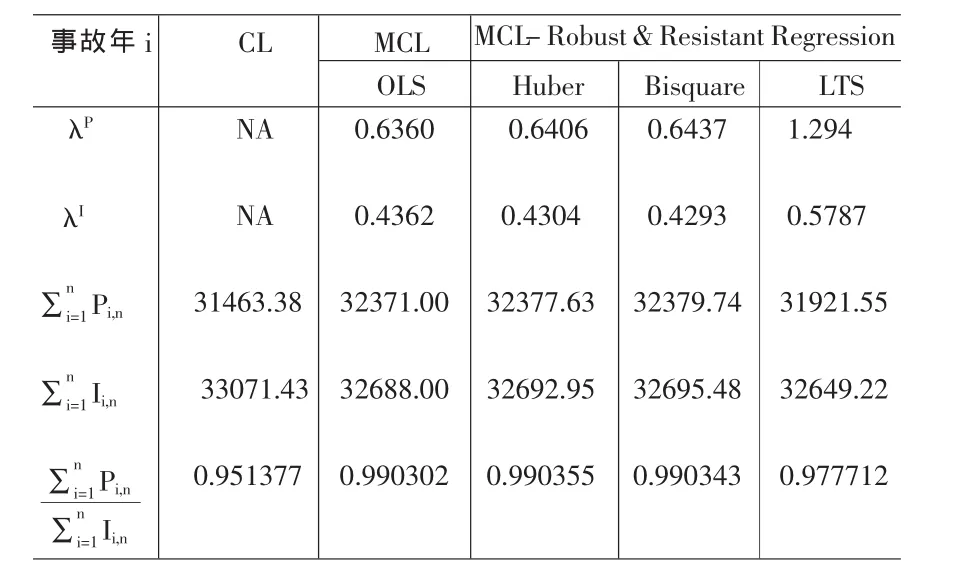
表6 CL、传统MCL和优化MCL方法的参数估计值
表5和表6表明,与传统链梯法相比,由Munich链梯法得到的每一事故年的最终赔款额P/I的比率和所有事故年平均最终赔款额的P/I比率均更接近于1,因此Munich链梯法能够很好地解决传统链梯法中分别依据已决赔款数据和已发生赔款数据预测的最终赔款额相差较大的问题。同时,通过稳健回归(Huber M估计法和Bisquare M估计法)改进的Munich链梯法能够在一定程度上优化Munich链梯法,即通过降低离群点对参数估计的干扰增强最终赔款额预测的准确性,从而进一步提高最终赔款额的比率P/I。通过耐抗回归(LTS估计法)改进的Munich链梯法对此例的计算结果并不理想,但对存在显著离群点的数据进行参数回归估计时,采用该方法将得到理想的优化效果。
4 结论
本文采用Munich链梯法及其优化方法分别依据已决赔款数据和已发生赔款数据来预测最终的赔款额,进而得到未决赔款准备金的估计值。较传统链梯法,Munich链梯法及其优化方法具有以下特点:
(1)Munich链梯法依据已决赔款数据和已发生赔款数据的相关性来调整发展因子,从而成功地降低了链梯法基于已决赔款数据和已发生赔款数据得到的最终赔款额之间的差异。
(2)本文通过统计学中的稳健回归(Huber M估计法和Bisquare M估计法)和耐抗回归(LTS估计法)方法优化了Munich链梯法,即通过降低残差图中离群点对回归参数估计的干扰,增强回归模型的稳定性,从而减小最终赔款额的预测误差。
(3)Munich链梯法及其优化方法简单有效,可操作性强。由于本文应用R软件编译实现Munich链梯法及其优化方法,解决了矩阵处理和回归参数估计等问题,使得该方法具有很强的现实操作性。
[1]Halliwell,L.J.Conjoint Prediction of Paid and Incurred Losses[C].CAS Forum,1997.
[2]Quarg,G.,Mack,T.Munich Chain Ladder[J].Blatter der DGVFM,Band XXVI,2004,597~630.
[3]Verdier,B.,Klinger,A.JAB Chain:A Model Based Calculation of Paid and Incurred Developments Factors[C].36thASTIN Colloquium,2005.
[4]Rousseeuw,P.J.,Leroy,A.M.Robust Regression and Outlier Detection[M].New York:Wiley,1987.
[5]Markus Gesmann.Mack,Bootstrap and Munich-chain-ladder Methods for Insurance Claims Reserving[EB/OL].http://www.freestatistics.org/cran,2008.
