求解作业车间调度问题的改进蚁群算法

马 军，李 薇

(1.安徽财经大学 国际经济贸易学院，安徽 蚌埠 233041；2.安徽财经大学 商务学院，安徽 蚌埠 233030）

0 引言

作业车间调度问题(Job Shop Scheduling Problem，JSSP)是用m台机器(资源)来加工n个工件(任务)，并且每个工件又由k个工序组成，每个工序要按照一定的顺序来完成[1]。JSSP的调度目标是在满足各工序加工顺序约束条件下，确定每台机器上各工序的加工顺序及加工开始时间，并使某个性能指标最优，如制造周期最短[2]。作业车间调度问题是一类典型的复杂生产调度问题，具有约束松弛度紧、NP-Hard等特性[3]。近年来，各国尝试采用不同方法来求解作业车间调度问题，例如：遗传算法 (genetic algorithm)[4～6]、禁忌搜索(taboo search)[7,8]、蚁群算法 (ant colony optimization)[9,10]、演化算法(evolutionary algorithm)[11,12]以及模拟退火(simulated annealing)[13,14]等。各国学者通常使用各种混合方法来求解作业车间调度问题：(1)将现有方法进行一定程度地改进[15～17]；(2)将一些启发式规则集成到已有方法中[18～20]；(3)多种现有方法 的 混 合 集 成[7～9]。 在 求解复杂JSSP的过程中，JSSP的领域知识及专家的经验知识等对于最终的求解质量和求解效率都起着至关重要的作用。因此，考虑将领域知识和经验知识集成到蚁群算法中的尝试，具有重要的理论意义和实践意义。鉴于此，本文拟提出一种求解作业车间调度问题的改进蚁群算法。该方法将调度知识有效地融入到蚁群算法中，以期使其优化效率得到极大地改进。

1 改进蚁群算法

为了有效地求解JSSP，本文提出了一种改进蚁群算法。该方法将调度知识有效地融入到蚁群算法中，使得优化效率得到极大地改进。该方法的计算流程如图1所示。

1.1 调度知识表达

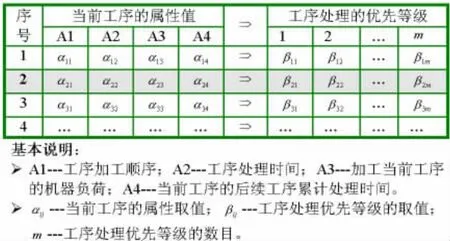
图2 调度知识的表达形式

本文将JSSP的领域知识及专家的经验知识等统称为调度知识。为了方便地实现优化过程中调度知识的挖掘、存储和应用，笔者采用图2所示的形式完成对调度知识表达。

工序处理优先等级的赋值有两种情况：(1)概率形式，表示给定属性的工序在某优先等级下加工的概率；(2)打分形式，表示给定属性的工序在某优先等级下加工的次数。为了便于后续的处理，笔者采用打分形式对工序处理优先等级进行赋值。图2中调度知识的含义如下 (采用打分形式，第2条调度知识的含义)：

如果

(工序x的工序加工顺序属性=α21)∧

(工序x的处理时间属性=α22)∧

(加工工序x的机器负荷属性=α23)∧

(工序x后续工序累计处理时间属性=α24)∧

则

(工序x以优先等级1加工的次数为 β21)∧

(工序x以优先等级2加工的次数为 β22)∧

(……)∧

(工序x以优先等级m加工的次数为β2m)。

1.2 状态转移规则

在描述状态转移规则之前，先定义工序的选择概率。在这里，笔者定义了两种工序选择概率：基于工序处理时间的工序选择概率和基于调度知识的工序选择概率。

所谓的妊娠合并糖尿病指的是:妊娠期间发现或发病的由不同程度糖耐量异常及糖尿病引起的不同程度的高血糖,其中有些患者在妊娠前便已经被诊断出患有糖尿病,在妊娠之后则有持续性加重的表现等[1-2]。为了研究妊娠与糖尿病的关系,从而提升临床治疗效果,本文在2015年12月-2016年12月间妇产科收治的80例妊娠合并糖尿病患者参与研究,探究其临床护理效果,具体研究内容阐述如下:

(1)基于工序处理时间的工序选择概率。在t次迭代时，蚂蚁k选择工序j的概率公式为：

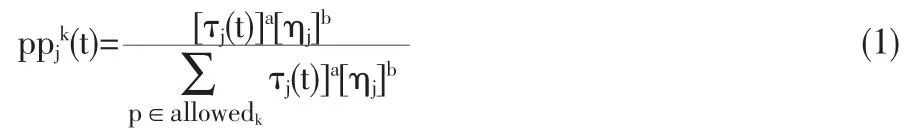
这里，allowedk表示蚂蚁k在当前位置(当前时刻的特定机器)上可处理工序的集合；τj(t)表示t时刻工序j上的信息素水平；ηj=1/tj表示工序加工时间的倒数；a,b分别表示工序j的信息素启发值和加工时间启发值的权重。

(2)基于调度知识的工序选择概率。在t次迭代时，蚂蚁k选择工序j的概率公式为：

这里，γj表示根据当前的调度知识，处理工序j的优先等级的综合评估值；a,b分别表示工序j的信息素启发值和调度知识启发值的权重；βji表示工序 j的第i个处理优先等级的取值；wi表示第i个处理优先等级的权重。

表1 本文的5种不同的实验方案

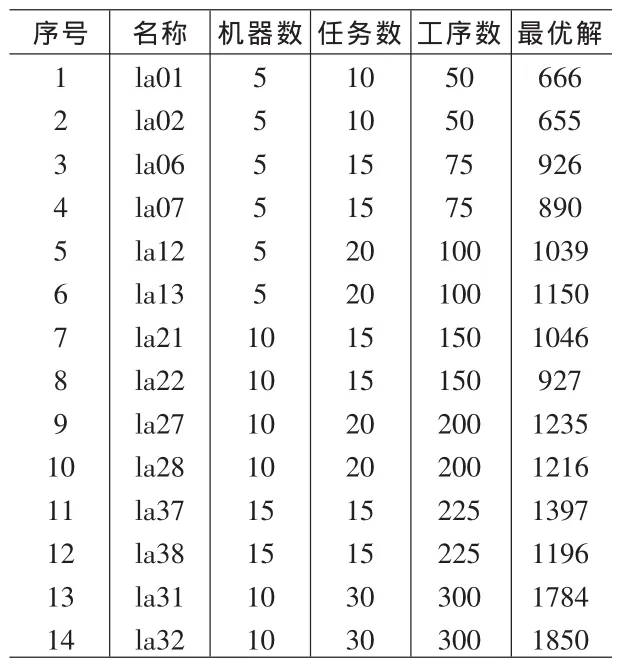
表2 本文用到的14个测试实例

表3 本文蚁群算法中的参数设置

本文的状态转移规则如下：在t次迭代时，蚂蚁k依据以下状态转移规则来选择下一个需要处理的工序

这里的q为[0,1]范围内服从均匀分布的一个随机数；q0是一个设计参数，q0=lg(Gen)/lg(Max_Gen)；Gen表示当前的迭代次数，Max_Gen表示用户设定的最大迭代次数。

1.3 信息素局部更新规则

这里的h表示在第t次迭代的最优可行方案中，工序j在给定机器上的加工次序；H表示所有任务的最大工序数。

1.4 信息素全局更新规则

在蚁群算法中，信息素全局更新规则仅用于更新当前最优可行方案的信息素水平。

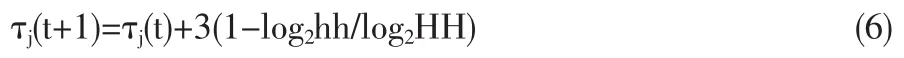
这里的hh表示在当前最优可行方案中，工序j在给定机器上的加工次序；HH表示所有任务的最大工序数。

1.5 信息素衰退规则

本文将每个工序上的信息素都控制在范围[τmin,τmax]内。

这里ρ(0＜ρ＜1)表示信息素衰减因子。

1.6 调度知识的挖掘

为了有效地挖掘、存储和应用调度知识，笔者对每个工序属性指标都进行了离散化操作。根据不同的优化需求，每个工序属性指标都被划分为若干个不同的水平(将每个工序属性指标的取值范围分割成若干个区间)。同时，本文采用多维数组来记录和存储调度知识(图3)。调度知识挖掘的计算流程如图4所示。

2 仿真实例

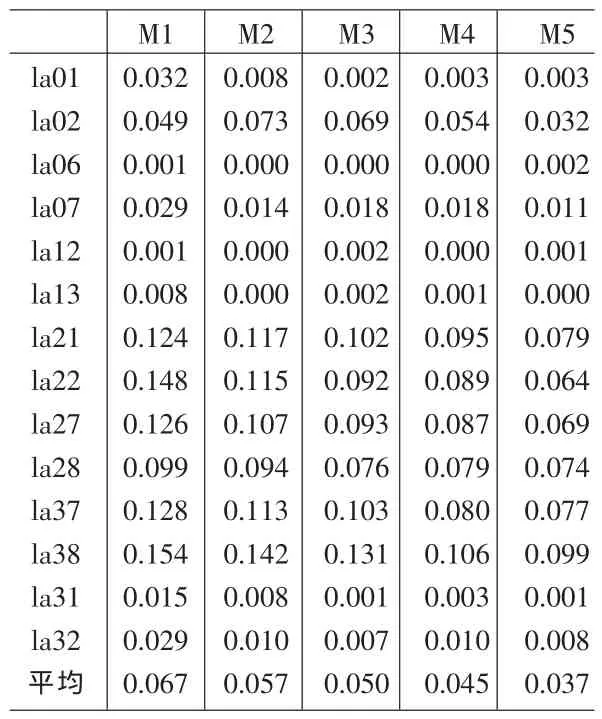
表4 采用5种实验方案求解14个测试实例的优化误差

为了验证本文方法的有效性，笔者设计了5种不同的实验方案(表1)。表1中调度知识 i(1≤i≤4)的含义是：在该调度知识中，工序属性指标被分为i+1个水平，工序处理优先级被分为2(i+1)个等级。在对经验知识进行综合评估时，工序处理优先等级的权重wi=5(mi+1)，1≤i≤m，这里的m表示工序优先处理等级的数目。笔者采用14个典型实例(表2)来验证各种实验方案，改进蚁群算法的参数设置见表3。

表4和表5列举了本文的试验结果。从表4中可以看出，调度知识表述的越详细，平均优化误差越小。这表明：将调度知识融入到蚁群算法中，可以有效提高蚁群算法的优化绩效。从表5中可以看出，无论是优化时间还是优化结果，本文提出的改进蚁群算法都要优于现有的标准蚁群算法。

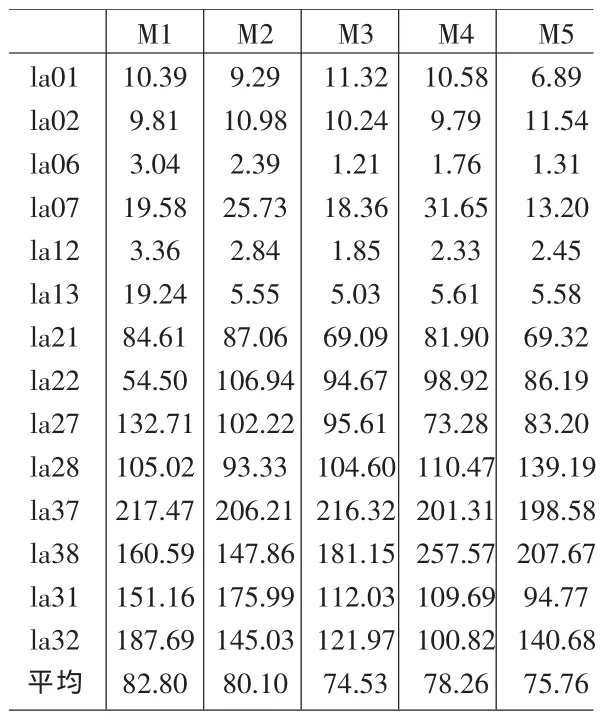
表5 采用5种实验方案求解14个测试实例的优化时间

3 结束语

本文的主要创新点是：采用一种改进蚁群算法来求解作业车间调度问题。通过将调度知识有效地融入到蚁群算法中，使得改进蚁群算法在优化效率上大大改进。

[1]Tavakkoli-Moghaddam R.,Daneshmand-Mehr M.A Computer Simulation Model for Job Shop Scheduling Problems Minimizing Makespan[J].Computers&Industrial Engineering,2005,48.

[2]王秀宏,乔清理,王正欧.Job-shop调度问题的瞬态混沌神经网络解法[J].系统工程,2001,19(3).

[3]Watanabe M.,Ida K.,Gen M.A Genetic Algorithm with Modified Crossover Operator and Search Area Adaptation for the Jobshop Scheduling Problem[J].Computers&Industrial Engineering,2005,48.

[4]Goncalves J.F.,De Magalhaes Mendes J.J.,Resende Gcm.A Hy-brid Genetic Algorithm for the Job Shop Scheduling Problem[J].European Journal of Operational Research,2005,167.

[5]杨晓梅,曾建潮.采用多个体交叉的遗传算法求解作业车间问题[J].计算机集成制造系统,2004,10(9).

[6]姜思杰,徐晓飞,李全龙.基于遗传优化算法求解作业车间调度问题[J].计算机集成制造系统,2002,8(3).

[7]Pezzella F.,Merelli E.A Tabu Search Method Guided by Shifting Bottleneck for the Job Shop Scheduling Problem[J].European Journal of Operational Research,2000,120.

[8]梁旭,黄明.禁忌-并行遗传算法在作业车间调度中的应用[J].计算机集成制造系统,2005,11(5).

[9]Huang K.L.,Liao C.J.Ant Colony Optimization Combined with Taboo Search for the Job Shop Scheduling Problem[J].Computers&Operations Research,2008，35（4）.

[10]王常青,操云甫,戴国忠.用双向收敛蚁群算法解作业车间调度问题[J].计算机集成制造系统,2005,10(7).

[11]Tanev I.T.,Uozumi T.,Morotome Y.Hybrid Evolutionary Algorithm-Based Real-World Flexible Job Shop Scheduling Problem:Application Service Provider Approach[J].Applied Soft Computing,2004,(5).

[12]何霆,刘文煌,梁力平.基于进化算法的一类作业车间调度[J].计算机集成制造系统,2001,7(1).

[13]KoLonko M.Some New Results on Simulated Annealing Applied to the Job Shop Scheduling Problem[J].European Journal of Operational Research,1999,113.

[14]吴大为,陆涛栋,刘晓冰.求解作业车间调度问题的并行模拟退火算法[J].计算机集成制造系统,2005,11(6).

[15]张超勇,饶运清,李培根.求解作业车间调度问题的一种改进遗传算法[J].计算机集成制造系统,2004,10(8).

[16]冯奇峰,李言.运用带有记忆库的遗传算法求解作业车间调度问题[J].计算机集成制造系统,2005,11(8).

[17]范路桥,常会友,朱旭东.一种改进的作业车间调度算法及其实现[J].计算机集成制造系统,2005,11(5).

[18]Lee D.S.,Vassiliadis V.S.,Park J.M.A Novel Threshold Accepting Meta-Heuristic for the Job-Shop Scheduling Problem[J].Computers&Operations Research,2004,(31).

[19]代勇,付宜利,马玉林.与启发式规则相结合的遗传算法在车间调度问题中的研究[J].现代制造工程,2003,(3).

[20]吕文彦,党延忠.基于综合规则与遗传算法的可重入生产系统调度[J].计算机工程,2005,31(13).