欠采样在基带预失真功率放大器线性化的应用

(电子科技大学 空天科学技术研究院,成都 610054)

1 引 言

随着移动通信事业的快速发展，特别是TDS CDMA等下一代移动通信技术的发展[1-2]，使得系统对功放线性的要求越来越高。在移动通信系统中，如果采用一般的高功率放大器(通常工作于AB类)将由于非线性的影响产生频谱再生效应，为了较好地解决信号的频谱再生和误差矢量幅值(EVM)问题，就必须对功放采用线性化技术。近年来，基带预失真技术因其同时具有线性好、效率高、体积小、实现简单等独特优点而得到了快速发展。预失真较前馈等其它线性化方法效率更高、成本更低[3-4]，有着更广的应用前景。

在基带预失真结构中对功率放大器输出失真信号的采样率是一个非常重要的问题，现代通信的带宽越来越宽而非线性系统经常引起频谱扩展，使得输出信号的带宽远大于输入信号的带宽，当利用数字信号处理技术对这些非线性进行检测和补偿时，不得不选择输出信号的Nyquist采样率、N倍输入信号的Nyquist采样率[5-6]，增加了系统的成本和复杂度。本文将证明非线性系统的输出信号可以在输入信号的采样率下检测并被补偿，在朱氏通用采样定理[7]里得到证明并在测试中验证。

本文提出了一种将欠采样应用到基带预失真功率放大器设计的新方法，在不影响预失真的性能下降低了采样率的要求从而降低系统成本和复杂度。本文首先介绍欠采样的原理，证明欠采样在基带预失真中的可行性，然后计算欠采样计算误差，最后在基带预失真中应用欠采样，验证欠采样的可行性。

2 基带预失真功率放大器设计

2.1 基带预失真基本原理和结构

预失真技术是结构最为简单的射频功放线性化技术，其原理框图如图1所示。预失真技术是通过在放大器前端添加一个特性和放大器特性互逆的非线性单元来抵消放大器的失真，非线性单元称为预失真器。输入信号Vi经过预失真器后产生增益扩张的预失真信号Vp，Vp再经过有增益压缩非线性的放大器进行放大，最终得到线性化的输出信号Vo。其中，预失真器和放大器的传递函数满足：

F(|Vi|)G(|Vp|)=k

式中，k为常数。

图1 数字预失真原理图Fig.1 The digital predistortion principle diagram

2.2 欠采样原理

欠采样时会发生频谱混叠，这种混叠产生的信号失真是不能通过低通滤波器恢复的。令x(t)为任一函数，最高频率为f0，其Nyquist采样率为2f0，通过香农采样定理其信号可恢复为

(1)

1992年，ZHU Yang-ming发表了“通用采样定理”[7-8]，若y(t)为任一函数，带通或非带通，如图2所示，存在一个连续的一一映射函数如f(y(t))为带限的，即傅里叶变换:

Fy(y(t))=0，f≥F0

(2)

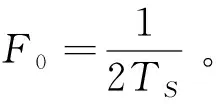
则y(t)可由其在f(y(t))的Nyquist采样率下的采样y(nTS)唯一决定。

图2 朱氏通用采样原理框图
Fig.2 Zhu′s generalised sampling theorem

对于功率放大器来说，可以认为其在饱和输入点内，其输入输出特性为严格单调增函数，即一一映射，那么对比图1和图2，可以令g(t)为功率放大器的输入输出函数，f(t)为理想的预失真函数，即g(t)的反函数，则输入信号x(t)通过预失真变换为x′(t)输入功率放大器，通过功率放大器的非线性变换g(t)=f-1(t)输出为y(t)，其中f-1(t)为f(t)的反函数。那么根据朱氏通用采样定理，y(t)可由在x(t)的采样率下采样后唯一决定，并可由式(2)恢复：

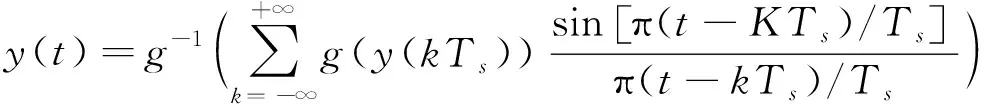
(3)

同样，y(t)在x(t)的采样率下可用于功率放大器的非线性识别并用于功放线性化的自适应算法，其原理如图3所示。

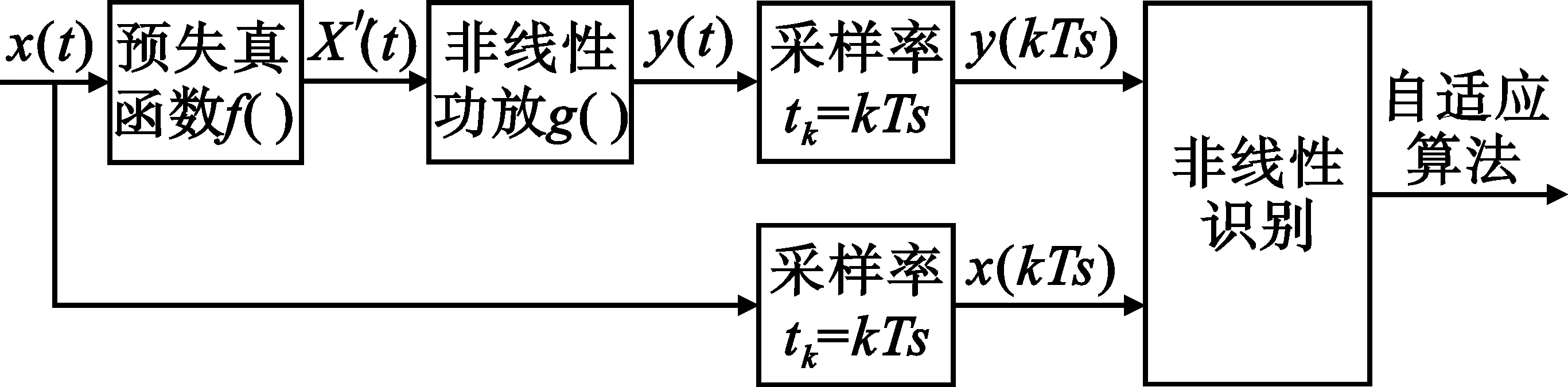
图3 在输入信号Nyquist采样率下的非线性采样Fig.3 Sampling at input signal Nyquist rate for nonlinearity sampling

2.3 系统构建

为验证欠采样后基带预失真线性化的性能，构建如图4所示的基带预失真功率放大器系统。基带预失真的结构取决于发射机的结构，基带的正交调制信号由调制器正交调制到射频，由功率放大器放大输出。其中基带预失真部分采用极坐标复增益预失真技术，由FPGA实现查找表索引部分功能，输入信号与增益查找表中系数相乘，然后与相位查找表调制得到预失真的信号，其系数通过输入信号幅度索引选择。功率放大器由于老化或温度漂移，需要对预失真进行自适应控制以保证对非线性补偿的效果。本方案中对功率放大器输出信号进行采样，然后与输入信号相比较提取功率放大器输出的非线性分量，并在DSP完成预失真自适应算法。

图4 数字预失真功率放大器原理图Fig.4 Digital predistortion power amplifier diagram

由于功率放大器的非线性对输入信号有频谱扩展作用，为采样到五阶交调失真信号，输出信号的采样率一般为3～5倍输入信号的Nyquist采样率，本文通过仿真及实验对比，证明采用输入信号的Nyquist采样率对功率放大器非线性输出信号进行采样可行。

3 仿真实验结果

对所选的功率放大器进行仿真以验证其结果的准确性。基于欠采样的预失真方法，在Matlab中对预失真进行了仿真，功放失真模型采用Saleh模型，幅度和相位失真分别为

(4)

预失真器采用基于极坐标的幅度和相位多项式模型，即幅度和相位的非线性特性，各用一个关于信号幅度的实系数多项式来描述，采用LMS自适应算法，分别得到功放的AM/AM和AM/PM特性的多项式逆模型，然后把预失真器加在功放之前。

图5 欠采样和过采样下基带预失真效果图Fig.5 Spectrum of compensated amplifier output under oversampling and undersampling

输入双音信号，通过Matlab对图3所表示的系统进行仿真，如图5所示，在欠采样和过采样下基带预失真的线性化效果相同。

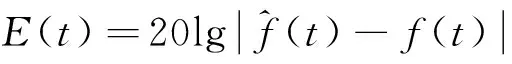
经朱氏采样定理进行仿真，其误差结果如图6所示，从图中可看出，欠采样的误差对其失真信号的表达和计算影响较小。

图6 信号重建后的误差幅度Fig.6 The error amplitude after signal reconstruction

在中心频率为2.14 GHz、间隔为500 kHz、输出功率为50 W的功率放大器系统中进行双音测试，未加预失真前，放大器三阶交调失真为27 dBc；加入基带预失真后，三阶交调为46 dBc，改善了19 dB，与利用功率放大器的输出Nyquist采样率下失真信号的改善度相比降低2 dB左右，仍满足系统指标要求。

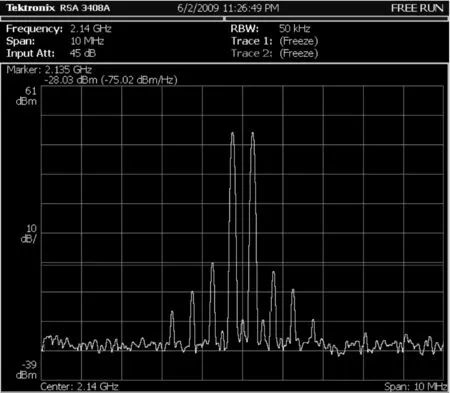
图7 经过欠采样基带预失真线性化后的频谱Fig.7 Spectrum of compensated amplifier output after undersampling

4 结 论

本文从朱氏通用采样定理中推出，在非线性系统中仅用输入信号的Nyquist采样率对输出信号进行采样即可实现输出信号非线性分量的识别和补偿。在本文的例子中，将功率放大器进行无记忆非线性建模，对功率放大器输出信号在两个频率进行采样，第一种用输入信号的Nyquist采样率进行采样，第二种用输出信号的Nyquist采样率即包括三阶、五阶交调信号的采样率，两种情况下自适应预失真补偿非线性的结果一致。本文给出了非线性功率放大器输出信号的最低采样率。利用该技术大大降低了对失真信号采样率，同时也降低了基带预失真的成本并简化了电路。

参考文献：

[1] Khan A H,Qadeer M A,Ansari J A, et al. 4G as a Next Generation Wireless Network[C]//Proceedings of 2009 International Conference on Future Computer and Communication. Kuala Lumpar:[s.n.],2009: 334-338.

[2] Bill Krenik.4G Wireless Technology:When will it happen? What does it offer[C]//Proceedings of 2008 IEEE Asian Solid-State Circuits Conference. Fukuoka:IEEE,2008:141-144.

[3] Mazen Abi Hussein, Yide Wang, Georges Peyresoubes. LUT/Parametric Digital Predistortion Approach for the Linearization of Power Amplifiers Characteristics[C]//Proceedings of the 38th European Microwave Conference. Amsterdam:[s.n.],2008:571-574

[4] Wu Shanying, Simon Hau S F, Wong Y M. The effect of D/A accuracy on the performance of digital predistortion for RF power amplifiers[C]//Proceedings of 2006 IEEE International Symposium on Circuits and Systems.[S.l.]:IEEE,2006: 1378-1382.

[5] Billings S A,Fadzil M B. The practical identification of systems with nonlinearities[C]//Proceedings of IFAC Conference on Dentification System Parameter Estimation.New York:[s.n.],1985:155-160.

[6] Tsimbinos J, Lever K V. Applications of higher-order statistics to modeling, identification and cancellation of nonlinear distortion in highspeed samplers and analogue-to-digital converters using the Volterra and Wiener models[C]//Proceedings of IEEE Signal Processing Workshop Higher Order Statist.South Lake Tahoe, CA:IEEE,1993: 379-383.

[7] Zhu Y M.Generalized Sampling Theorem[J]. IEEE Transactions on Circuits System-II:Analog and Digital Signal Processing, 1998,45(8): 959-969.