利用自相关矩阵的量化合作频谱感知方法
2010-09-27
(解放军电子工程学院,合肥 230037)
1 引 言
认知无线电[1](Cognitive Radio, CR)是一种用于提高频谱利用率的智能无线电技术,其应用和发展前景广阔,是当前研究热点之一[2]。
频谱感知[3-4](Spectrum Sensing)也称频谱检测,是认知无线电的一项关键技术,其主要任务是从多域频谱空间中获得频谱的使用情况。经典的检测方法有匹配滤波检测[5]、能量检测[6]和循环特征检测[7]等,各有其优缺点。匹配滤波检测需知道主用户发射信号的先验信息,应用范围有限。能量检测(Energy Detection, ED)是最常用的一种检测方法,不需知道主用户信号先验信息,具有复杂性低、实现简单等优点,但需要知道噪声方差信息,不适于低信噪比情况,需克服噪声不确定性等问题。另外,能量检测对独立同分布的信号样本检测效果较好,但对相关信号的检测效果不是最优的。循环特征检测可以用来区分不同类型的发射信号,但需知道主用户信号的循环频率,且复杂度较高。
为了减小无线信道的阴影、衰落和时变特性对频谱检测的影响,研究人员提出了各种基于能量检测的合作式频谱感知方法[8-11]。另一方面,研究人员考虑将其它理论应用于频谱感知,Cardoso等人在文献[12]中提出了一种基于大维随机矩阵理论(RMT)的频谱感知算法,利用M-P律给出了大样本情况下的频谱检测方法,但不适用于小样本情况。新加坡电信研究院的研究人员也提出了一类基于RMT的频谱感知算法,包括协方差绝对值法(CAV)[13]和最大最小特征值法(MME)[14]等,这类算法考虑了实际应用中采样数有限的问题,但仅研究了单个CR用户的情况。
在分析了上述频谱感知算法的基础上,本文提出了一种基于自相关矩阵的量化合作频谱感知方法,称之为QCAM方法。建立了频谱感知模型,利用自相关矩阵构建了检验统计量,先对该检验统计量进行有限位的量化,再将该量化信息传送至融合中心采用“加权投票准则”进行融合,以提高系统的检测性能。该方法不需要知道主用户信号先验知识和噪声方差信息,是一种盲感知方法。
2 系统模型
2.1 合作频谱感知模型
假设一个CR网络,由若干个CR用户(本地检测器)和一个CR基站(融合中心)构成,网络中包括分离的数据信道和控制信道。
图1给出一种并行式合作频谱感知模型结构,SU1,SU2,…,SUN代表N个CR用户,各CR用户由无线环境获取原始观测数据或检测统计量,经本地判决得到本地判决信息u1,u2,u3,…,uN,将其送至融合中心经综合处理给出全局判决uc。

图1 并行式合作频谱感知模型Fig.1 Parallel cooperative spectrum sensing model
2.2 信号模型
假设我们感兴趣的频段中心频率为fc,带宽为B,对接收信号以采样频率fs(fs≥B)进行采样,则第i个CR用户n时刻的接收信号模型可表示为
(1)

2.3 检测统计量的构建
对第i个CR用户的接收信号,考虑L个连续样本,L称为平滑因子[13],构成如下向量:
Yi(n)=[yi(n)yi(n-1) …yi(n-L+1)]T
(2)
Xi(n)=[xi(n)xi(n-1) …xi(n-L+1)]T
(3)
ηi(n)=[ηi(n)ηi(n-1) …ηi(n-L+1)]T
(4)
构建信号和噪声的统计自相关矩阵如下:
(5)
(6)
(7)
式中,T表示共轭转置,IL表示L阶的单位阵。通常,信号与噪声之间是统计独立的,由此可得:
(8)
这样,若信号x(n)不存在,则RXi=0,矩阵RYi的非对角元素全为零;假设信号样本之间是相关的,则RXi为非对角阵,当信号x(n)存在时,矩阵RYi的非对角元素不全为零。据此,我们可以构建合适的检测统计量来判决主用户信号的存在与否。
实际应用中,可供使用的样本数是有限的。假设接收信号是随机平稳遍历过程,我们可以用样本自相关近似代替统计自相关,取
(9)
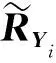
(10)
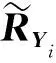
(11)
(12)
(13)
3 QCAM方法
3.1 总体方案
总的来说,QCAM方法可分为基于自相关矩阵的本地量化检测和融合判决两大部分,图2给出了QCAM方法的总体方案设计框图。首先,各CR用户利用接收到的信号r1(t),r2(t),…,rN(t),计算自相关矩阵并提取检测统计量,经本地量化检测得到本地量化判决信息u1,u2,…,uN,将其通过控制信道送至CR基站,然后,CR基站依据“加权投票准则”对接收到的判决信息进行融合判决,最终给出全局判决uc。为了便于讨论,假设量化判决信息在由CR用户向融合中心传送过程中不发生错误。
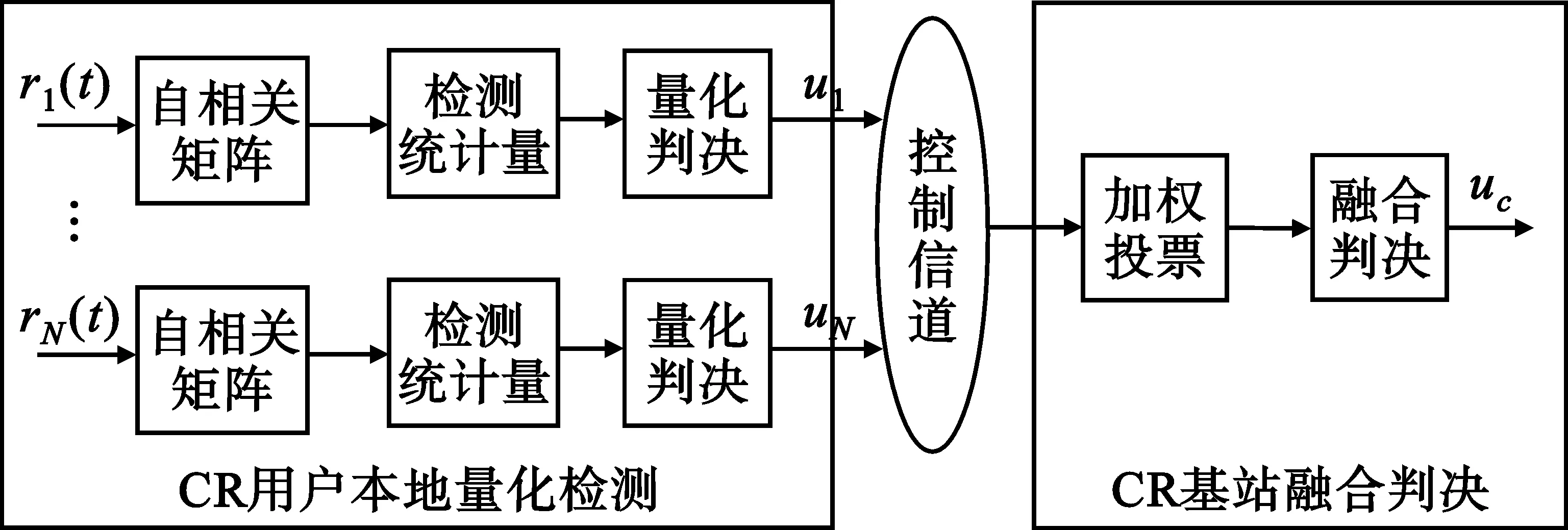
图2 QCAM方法总体方案框图Fig.2 Block diagram of QCAM
3.2 本地量化检测

(14)
式中,ui用十进制数表示,向认知基站传送的是其二进制表示形式。
为具体分析该方案的检测性能,本文以一种2 bit量化方案为例进行讨论。图3示意了2 bit本地量化检测方案的原理,与传统只用一个门限的硬判决方案不同,该方案采用了3个门限,分别为λ1、λ2和λ3,将整个观测空间划分为4个子空间,即Ω(0)、Ω(1)、Ω(2)和Ω(3)。

图3 2 bit量化检测方案原理Fig.3 Principle of 2 bit quantized detection scheme
为了便于讨论,假设各CR用户的本地量化规则相同。这样,每个CR用户需要发送2 bit信息以指示其检验统计量落在哪个子空间。给各子空间赋予不同的权重,如ω0=0,ω1=1,ω2=C,ω3=2C,其中,C∈Z(C>1)为待优化的设计参数,称为调权参数。
3.3 融合判决
在传统的中心式合作感知方案中,融合中心常采用“OR准侧”进行融合判决,与之不同,这里对各CR用户送来的信息采用“加权投票准则”进行融合:
(15)
式中,Nj(0≤j≤3)表示认知用户中检验统计量落在子空间Ω(j)的个数,Nc为加权投票结果,设融合中心判决规则为
(16)
式中,η为融合中心判决门限。这里,不妨取η=2C。
4 门限确定和理论分析
4.1 门限确定

(17)
(18)
由文献[13]可推知,在假设H0情况下,即主用户信号不存在时,有下列式子成立:
(19)
(20)
(21)
通常,M很大时,依据中心极限定理,Ti2近似服从高斯分布,即:
这样,对于CR用户对应门限λl(1≤l≤3)的本地虚警概率Pfl,可以得到:

(22)
可得:
(23)
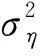
4.2 理论分析
在N个CR用户组成的认知网络中,需满足全局虚警概率PF的要求。假设当前主用户信号不存在,应没有CR用户的检验统计量落在子空间Ω(3),设有s个CR用户落在子空间Ω(2),t-s个CR用户落在子空间Ω(1),其余N-t个CR用户落在子空间Ω(0),即N3=0,N2=s,N1=t-s和N0=N-t,则:
Nc=(t-s)ω1+sω2=t-s+sC
(24)
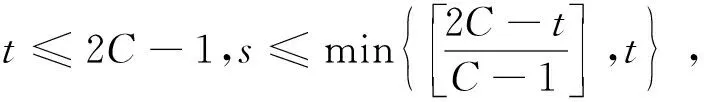
若定义认知概率PC=1-PF,则PC可以由式(25)求得:

N2=s,N3=0|H0)=
(25)
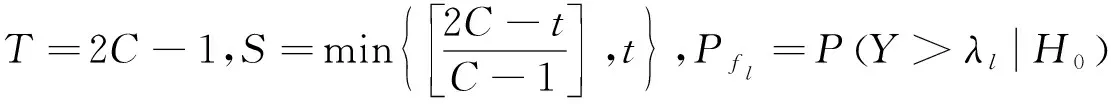

1-PF1+ρN=
(26)
当给定N、PF、C、β1和β2时,从式(25)中可以得到唯一的ρ值,从而获得Pfl(1≤l≤3),再依据式(23),可求得门限λl(1≤l≤3)。
假定所有的CR用户都经历独立同分布的衰落信道,则CR网络总的平均检测概率可由式(27)得到:

N2=s,N3=0H1)=
(27)

5 仿真结果及分析
在仿真实验中,假设在加性高斯白噪声(AWGN)环境下,待检测的主用户信号为一窄带信号,中心频率fc=100 MHz,带宽为B=4 MHz,采样频率fs=10 MHz。设定虚警概率PF=0.001,取平滑因子L=10,样本数M=40 000,CR用户数N=6,调权参数C=2,相对虚警比β1=0.25,β2=0.1。
作为对比,同时对能量检测的性能也进行了仿真,能量检测法门限λED可参照文献[15]进行设定:
(28)
(29)
噪声不确定性(单位dB)可表示为
b=max{10lgα}
(30)
其中,α∈[10-b/10,10b/10]。
图4给出了不同检测方案下平均检测概率随信噪比(SNR)的变化情况,其中,QCAM-1bit和QCAM-2bit分别表示采用1 bit量化和2 bit量化的QCAM方案,ED-OR表示没有噪声不确定性的OR准则合作式能量检测方案,ED-1dB和ED-2dB分别表示噪声不确定性为1 dB和2 dB的OR准则合作式能量检测方案。

图4 不同方案的检测性能比较Fig.4 Detection performance comparison
由图4可以看出:
(1)QCAM-2bit的性能要优于QCAM-1bit的性能,表明量化位数越多,检测性能越好,但这是以牺牲系统复杂度和通信开销为代价的;
(2)ED-1dB和ED-2dB的性能明显不如ED-OR的性能,表明能量检测对噪声不确定性很敏感;
(3)QCAM-1bit的性能优于ED-1dB和ED-2 dB的性能,表明QCAM可以克服低信噪比和噪声不确定性的影响;
(4)对于文中仿真所采用的相关窄带信号,QCAM-2bit的检测性能始终比ED-OR的检测性能好,但这不是在任何情况下都成立的,当信号样本间的相关性很弱时,能量检测将占优,对于完全独立的信号,QCAM方案将失效。
固定SNR为-8 dB,图5给出了QCAM-2bit方案和ED-OR合作检测方案的接收机工作特性(Receiver Operating Characteristic,ROC)曲线,由ROC曲线可以看到QCAM-2bit方案的性能具有显著优势。

图5 两种检测方案的ROC曲线Fig.5 ROC of two detection schemes
对于基于自相关矩阵的量化合作频谱感知方法(QCAM方法),需要说明以下几点:
(1)文中主要对2 bit量化合作频谱感知方案进行了具体分析,若希望进一步提高系统的检测性能可增大k值,但需要以牺牲通信开销和系统复杂度为代价;
(2)仿真中采用的是窄带信号,样本相关性较强,也可以采用其它信号,如文献[13]中采用的DTV信号,此时由于信号样本的相关性较弱,QCAM方案性能将可能不如理想状态下的合作式能量检测。但实际上,一是很难对噪声方差信息精确估计,二是待检测的信号往往是相关的,所以,QCAM方法还是具有较大应用潜力的;
(3)可以进一步仿真样本数和平滑因子对QCAM方案和ED方案检测性能的影响;
(4)在实际应用中,对于各子空间赋予的权重ωj、调权参数C和融合判决门限η,均可根据需要进行设置,甚至可以运用神经网络等智能算法进行优化。
6 结束语
频谱感知技术是认知无线电的核心,本文分析了现有频谱感知算法面临的一些问题,提出了一种基于自相关矩阵的量化合作频谱感知方法,该方法不需要知道主用户信号的先验知识和噪声方差信息,也不要求精确同步,同时折衷考虑了本地检测信息完整程度和通信开销的问题,并充分利用了多个CR用户的量化检测信息进行共享合作以提高频谱感知的性能。理论分析和计算机仿真结果表明,对于相关信号,该方法比能量检测方案的检测性能优越,且计算复杂度较低。所提算法的不足之处在于不能区分不同类型的信号,后续工作可考虑将其与其它方法结合起来对信号进行分步检测和识别。另外,控制信道的设计问题也有待进一步研究解决。
参考文献:
[1] Haykin S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2):201-220.
[2] 赵勇. 认知无线电的发展与应用[J]. 电讯技术,2009,49(6):93-101.
ZHAO Yong.Development Progress and Applications of Cognitive Radio[J].Telecommunication Engineering,2009,49(6):93-101.(in Chinese)
[3] Haykin S,Thomson J,Reed H.Spectrum sensing for cognitive radio[J].Proceedings of the IEEE,2009,97(5):849-877.
[4] Yücek T, Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys & Tutorials, 2009, 11(1):116-130.
[5] Cabric D, Brodersen R W. Physical layer design issues unique to cognitive radio systems[C]//Proceedings of IEEE International Symposium on Personal,Indoor and Mobile Radio Communications.Berlin,Germany:IEEE,2005:759-763.
[6] Digham F F, Alouini M S, Simon M K. On the energy detection of unknown signals over fading channels[J]. IEEE Transactions on Communications, 2007, 55(1):21-24.
[7] Kyouwoong K M, Akbar I, Baekyung K, et al. Cyclostationary approaches to signal detection and classification in cognitive radio [C]//Proceedings of New Frontiers in Dynamic Spectrum Access Networks. Dublin, Ireland: IEEE, 2007:212-215.
[8] Zheng X Q,Wang J L,Wu Q H,et al.A novel cooperative spectrum sensing algorithm in cognitive radio systems[J].Journal of Communications and Networks,2009,11(2):115-121.
[9] Gandetto M, Regazzoni C. Spectrum sensing: a distributed approach for cognitive terminals[J]. IEEE Journal on Selected Areas in Communications, 2007, 25(3):546-557.
[10] Mishra S, Sahai A, Brodersen R. Cooperative sensing among cognitive radios[C] //Proceedings of IEEE International Conference on Communications. Istanbul, Turkey: IEEE, 2006:1658-1663.
[11] Unnikrishnan J, Veeravalli V. Cooperative sensing for primary detection in cognitive radio[J]. IEEE Journal on Selected Areas in Signal Processing,2008, 2(1):18-27.
[12] Cardoso L S, Debbah M, Bianchi P. Cooperative spectrum sensing using random matrix theory[C]// Proceedings of ISWPC.Sautorini:IEEE,2008:334-338.
[13] Zeng Y,Liang Y C. Spectrum sensing algorithm for cognitive radio based on statistical covariances[J]. IEEE Transactions on Vehicular Technology,2009,58(4):1804-1815.
[14] ZENG Y,LIANG Y C.Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. IEEE Transactions on Communications, 2009,57(6):1784-1793.
[15] Ye Z, Memik G, Grosspietsch J. Energy detection using estimated noise variance for spectrum sensing in cognitive radio networks[C]//Proceedings of IEEE Wireless Communications and Networking Conference. Las Vegas, USA: IEEE, 2008:711-716.
