用于平面多层介质结构的全波算法*

(成都信息工程学院 通信工程系,成都 610225)

1 引 言

近年来低温共烧陶瓷(Low Temperature Cofired Ceramic, LTCC)技术在实际工程中得到了广泛应用，其电磁模型及特性引起人们的极大兴趣。LTCC多层基板为制造高密度微波多芯片组件(MMCM)的关键部件之一，多层介质的电磁特性将直接影响到MMCM的性能。寻求快速、准确的计算方法来分析多层介质的电磁特性，对于LTCC电路的设计具有重要指导意义。许多学者已在平面分层介质的研究方面做了许多卓有成效的工作,对各种计算方法进行了介绍[1-4],尤其在LTCC电路垂直互连的电磁特性研究方面进行了详细分析[5];离散复镜像方法(DCIM)在处理一层或两层介质的Green函数时非常有效[6],但在处理多层介质时,需要提取Sommerfeld 积分中的准静态项和表面波项,计算过程复杂。本文提出一种基于电场积分方程的平面多层介质带线结构全波分析算法，对LTCC多层平面带线结构进行了分析，并以一LTCC多层滤波器为仿真实例进行验证，结果表明该算法具有较好的速度和精度。

2 数值分析

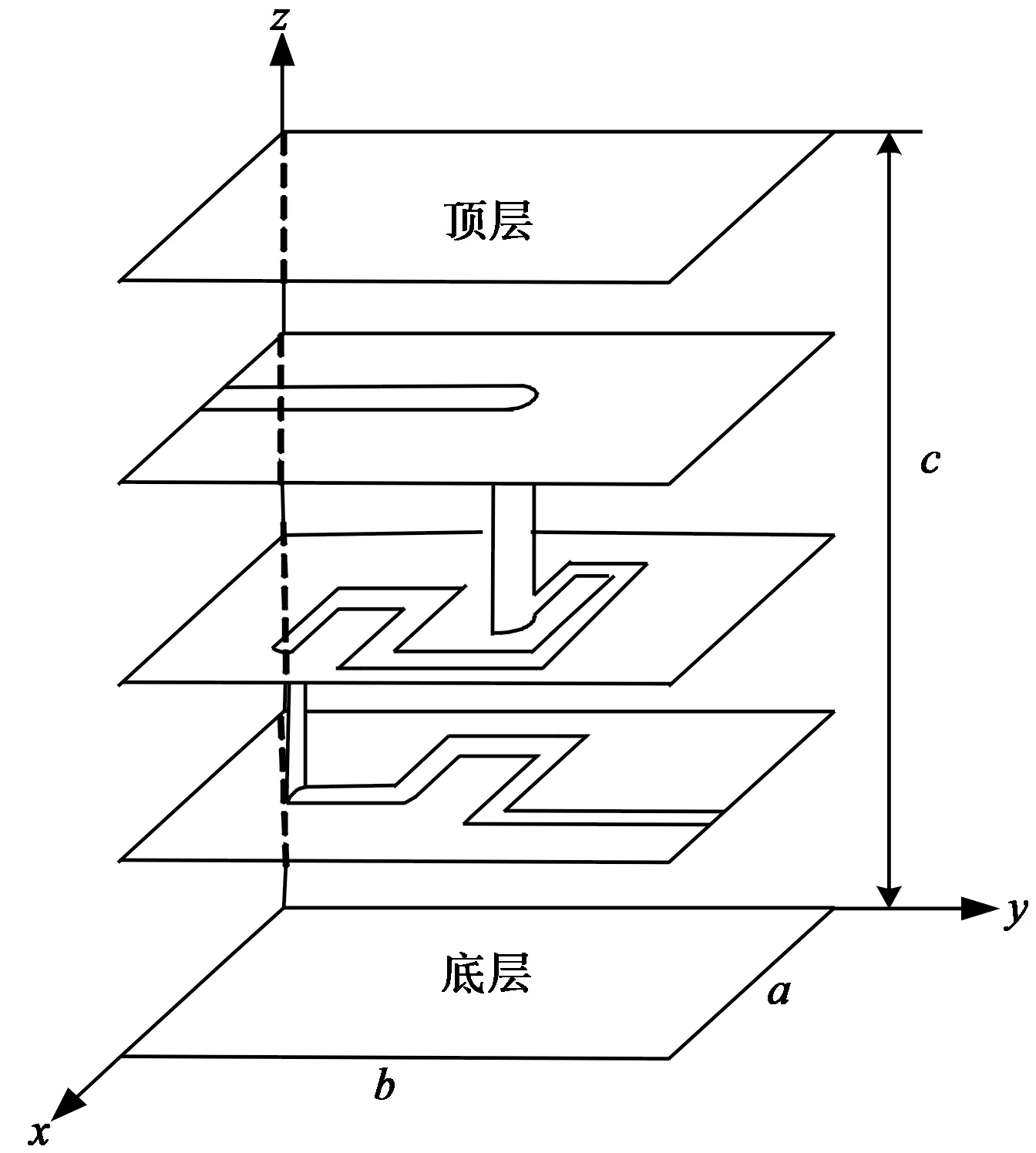
图1 一种典型的多层LTCC平面分层结构Fig. 1 Typical multilayer LTCC structure

一种典型的多层LTCC平面分层介质结构如图1所示。由图可见，电路拓扑结构中有平面导体，层间通过金属化垂直过孔连接。为分析简便起见，假设金属导体的厚度为零，电导率为无限大。若LTCC组件封装的顶层和底层之间距离小于十分之一波长，则在侧壁将不会产生任何辐射[4]。由此可知边界条件如下：

n×Ε=0，z=0,c

(1)

n×H=0，x=0,a

(2)

n×H=0，y=0,b

(3)

式(1)、(2)、(3)在求解式(4)所表示的Green函数中具有重要作用。

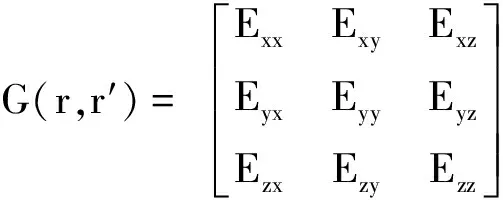
(4)

在x、y、z轴上分别施加激励源，可得到式(4)中的各个场分量，场分量的详细计算可以参见文献[6]。

假设有一个入射场Ei存在，则有：

(5)

式中，G(r,r′)是并矢格林函数，J(r′)为金属导带的面电流密度。对于沿x轴方向的微带线，微带线宽度比介质基片传输波长要小得多，则可把微带线上电流看成单方向的平行于x轴，可把J(r′)写成:

J(r′)=uxf(x′)g(y′)

(6)

式中,f(x′)是x′的未知函数，g(y′)假设为麦克斯韦分布:

(7)

式中,We是有效带宽，We=W+2δ，W为带线宽度；δ为考虑到由导带厚度引起的边缘效应所增加的半带宽。为用伽略金法解积分方程(5)，可将带线分成N个小段，将J(r′)按基函数展开：

(8)

式中，fn(x′)为分段正弦函数，即：

式中，lx为每小段的长度。将式(9) 代入到式(5)，再由伽略金法把基函数作权函数，则可将积分方程(5)变换为下列矩阵方程：

(10)

式中，[I]是未知系数矢量；[V]是外激励矢量；[Z]是阻抗矩阵，其矩阵元素为[7]

矩阵方程中[Z]及[V]已知，由此可算出

(12)

并把J的分布以及其它参数算出。

3 实例验证

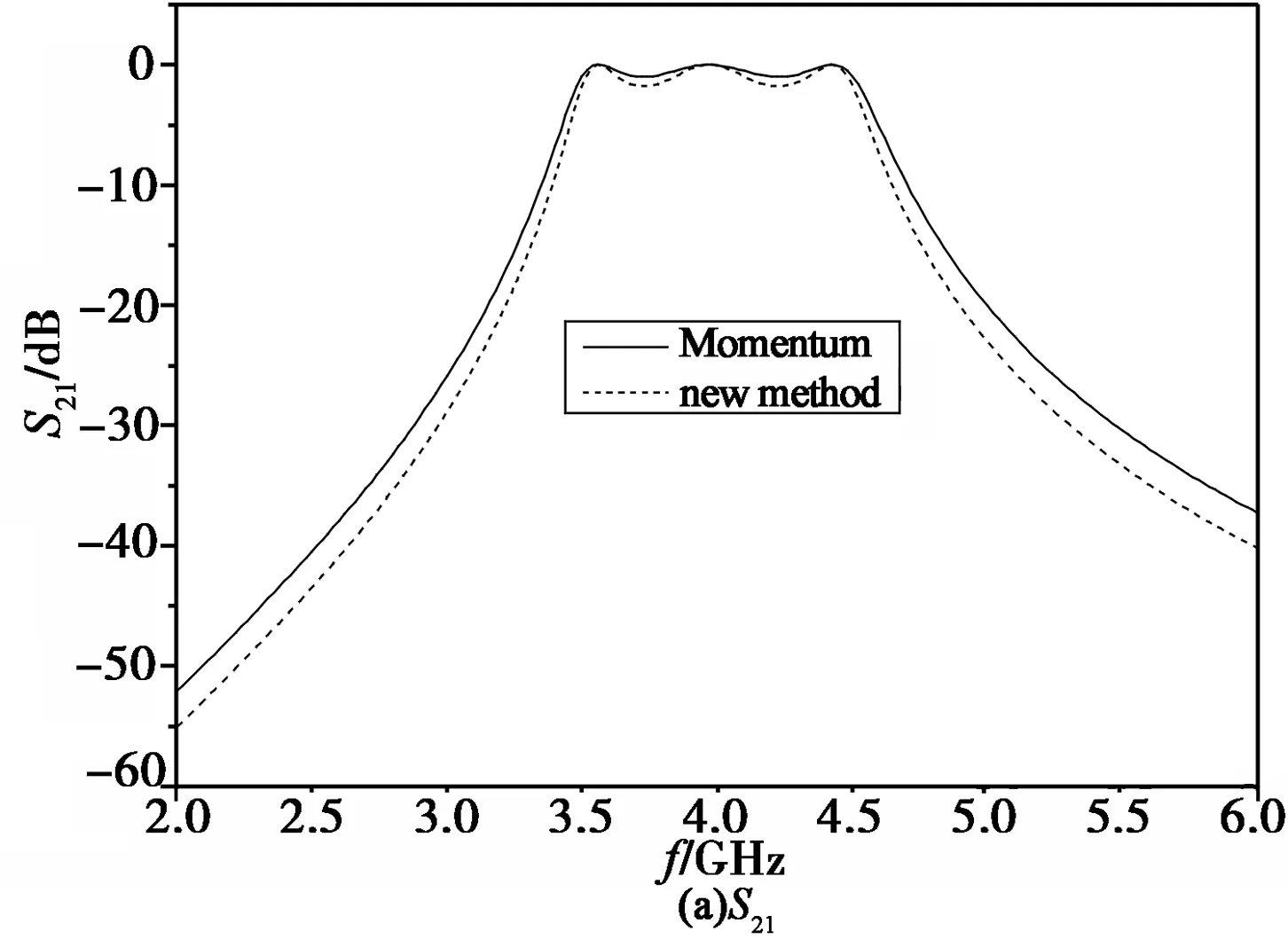
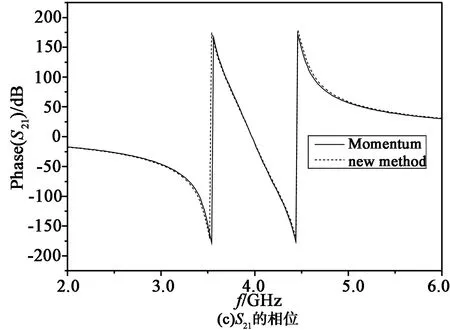
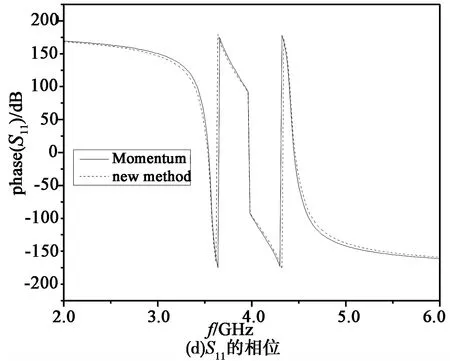
图2 本文方法和矩量法仿真结果比较Fig. 2 Comparison between this new method and Momentum method

以一个多层LTCC滤波器为例，通带为3.6～4.6 GHz，带内插损小于2.0 dB，波纹0.5 dB，带外抑制大于20 dB,采用文献[8]所描述的设计方法。运用前面的理论分析,对滤波器每层微带结构的格林函数进行仿真计算,由伽略金法最后求出其散射参数。为简化分析，我们假设介质均匀，并忽略介质损耗。为验证本文方法的可行性，也使用矩量法对滤波器进行了三维场仿真，仿真结果如图2所示。由图可见，在通带内，两者吻合较好，平均误差小于2%；阻带内两者的S21和S11幅度存在较小的偏离，但平均误差小于4%。随着频率的升高，两者在阻带外的偏差增大。分析是由于未考虑层间垂直互连拐角产生的不连续性效应以及电磁辐射效应所致。另外, 随着工作频率的升高,即使结构尺寸不变, 微带线等效电容的大小也会变化。同样，拐角处寄生电感也会随频率改变,如果电容、电感两者变化的趋势和速度不一致的话,则特性阻抗就不再保持一致从而导致误差增大。

据上述理论编程在Celeron 2.93 GHz CPU512 MHz内存的机器上运行，矩量法耗时5 min，本文方法只需3.0 min，表明该方法运算快速，精度较高。

4 结 语

本文提出一种基于电场积分方程的平面多层介质带线结构全波分析算法，并以一LTCC多层结构的滤波器为算例进行验证。与矩量法计算结果比较，具有运算速度快、精度高的特点。随着工作频率的增加，两者误差加大，层间垂直过孔互连的寄生参数效应及电磁辐射效应引入的误差不可忽视。因此必须建立更完整的电磁模型，才能获得更高频段的平面多层结构的准确电磁解。

参考文献:

[1] Okhmatovski V I, Cangellaris A C.A new technique for the derivation of closed-form electromagnetic Green′s functions for unbounded planar layered media [J]. IEEE Transactions on Antennas and Propagation,2002,50 (2): 1005-1016.

[2] Eibert T F,Hansen V.3-D FEM/BEM-hybrid approach based on a general formulation of Hygens’ principle for planar layered media[J]. IEEE Transactions on Microwave Theory Technology,1997, 45 (2) : 1105-1112.

[3] Khalil A I,Yakovlev A B,Steer M B.Efficient method of-moments formulation for the modeling of planar conductive layers in a shielded guided-wave structure[J]. IEEE Transactions on Microwave Theory Technology,1999, 47 (9): 1730-1736.

[4] Pereira Filho O M C,Sarkar T K. Full-wave analysis of MICs in multilayer dielectric media in a rectangular waveguide [J]. IEEE Transactions on Microwave Theory Technology, 2000, 48 (10): 1611-1622.

[5] Liu E X,Li E P,Li L W.Hybrid FDTD-MPIE method for the simulation of locally inhomogeneous multilayer LTCC structure [J]. IEEE Microwave Wireless Component Letters, 2005,15 (1) : 42-44.

[6] Kinayman N,Aksun M I.Efficient use of closed-form Green’s functions for the analysis of planar geometries with vertical interconnections [J]. IEEE Transactions on Microwave Theory Technology,1997, 45 (5) : 593-603.

[7] Harrington R F. Field computations by Moment Method [M].New York:Macmillan,1968.

[8] Tang Ching-Wen.Harmonic-Suppression LTCC Filter With the Step-Impedance Quarter-Wavelength Open Stub [J]. IEEE Transactions on Microwave Theory Technology,2004, 52 (2): 617-624.