一种新的OFDM系统优化脉冲成形方法*
2010-09-26
(郑州大学 信息工程学院,郑州 450001)
1 引 言
OFDM技术因其具有频谱利用率高、抗多径能力强、实现简单等特点,已成为下一代网络的关键技术之一。OFDM系统将输入的数据符号并行分配到多个并行的子信道上,并通过添加循环前缀(CP)很好地抑制了多径效应带来的时间弥散(频率选择性衰落)。但其较长的符号持续期使得OFDM系统对快时变信道导致的频率弥散(时间选择性衰落)更加敏感,特别是多普勒频移的影响。
因此,国内外学者提出脉冲成形OFDM(PS-OFDM)系统[1-5],它通过设计时频局域性较好的脉冲来减少双弥散(时间和频率弥散)信道带来的符号间干扰(ISI)和子载波间干扰(ICI)。文献[1,2]给出了LOFDM系统脉冲成形滤波器的设计方法,其采用非矩形时频网格,计算量较大,实现起来比较复杂;文献[3,4]利用ZAK变换构造时频优化滤波器,其实现仍比较繁琐;文献[5]研究了基于欠采样Gabor变换的双正交脉冲成形技术,可得到时频局域性较好的脉冲,但其频谱利用率较低。
本文提出了一种新的OFDM系统优化脉冲成形方法,通过对高斯脉冲成形滤波器与双弥散信道进行匹配,来抵抗信道干扰。仿真结果表明,采用该滤波器后的OFDM系统同传统的CP-OFDM系统相比可以获得较高的SIR,尤其在高频率弥散信道下,它能更好地抑制ISI和ICI。
2 时变信道与脉冲成形的时频关系描述
双弥散信道即线性时变信道通常采用随机变量参数——时延τ和多普勒频移ν来建模,得到随机信道模型S,若信道的输入信号为x(t),则该信道的输出信号为[7]
(1)
式中,s(τ,υ)称为时延-多普勒扩展函数,tm表示信道最大时延,亦称多径扩展,fd表示最大多普勒频移,亦称多普勒扩展,乘积tmfd为信道扩展因子。信道的时延扩展和多普勒扩展将导致符号间干扰和子载波间干扰,脉冲成形技术的目的是通过设计时频局域性均良好的成形滤波器,有效地改善调制信号的时频宽度使之匹配信道特性,从而解决时变信道带来的问题。
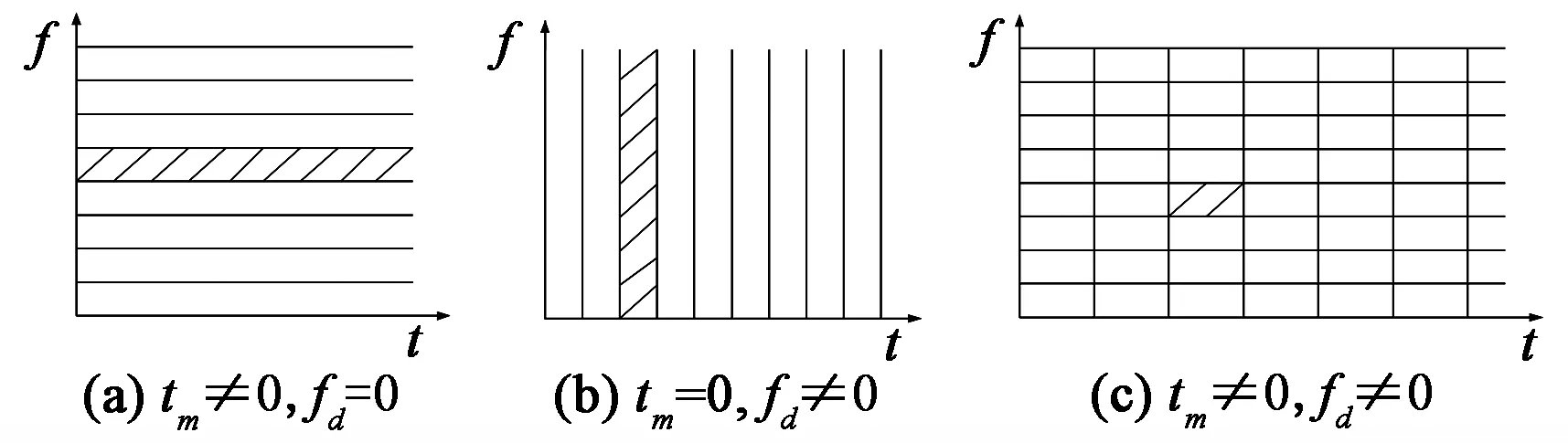
图1 信道与脉冲成形的时-频关系Fig.1 The time-frequency relationship of channel and pulse shaping
图1描述了3种情况下信道对脉冲成形时频特性的要求,阴影部分表示最优脉冲尺度。理想情况时信道是时间和频率非选择性衰落,则不会产生ISI和ICI。当信道仅是频率选择性衰落时,即tm≠0、fd=0,要求成形脉冲的频谱要窄,并采用频分复用技术(FDM),如图1(a)所示;当信道仅是时间选择性衰落时,即tm=0、fd≠0,要求成形脉冲的时宽要窄,并采用时分复用技术(TDM),如图1(b)所示;当信道是双弥散时,即tm≠0、fd≠0时,则要求脉冲成形函数具有良好的时频局域性,并在采用频分技术时选用成形脉冲保证时宽的局部性,如图1(c)所示。本文主要研究的内容就是双弥散信道下正交频分系统的脉冲成形技术,通过建立基于Gabor变换的OFDM系统模型,对Gabor基函数的时频局域性进行优化来解决信道的时间弥散和频率弥散。
3 基于Gabor变换的OFDM系统
3.1 系统描述
本文采用矩形时频网格来分析脉冲成形OFDM系统,图2给出了基于Gabor变换的OFDM系统框图。
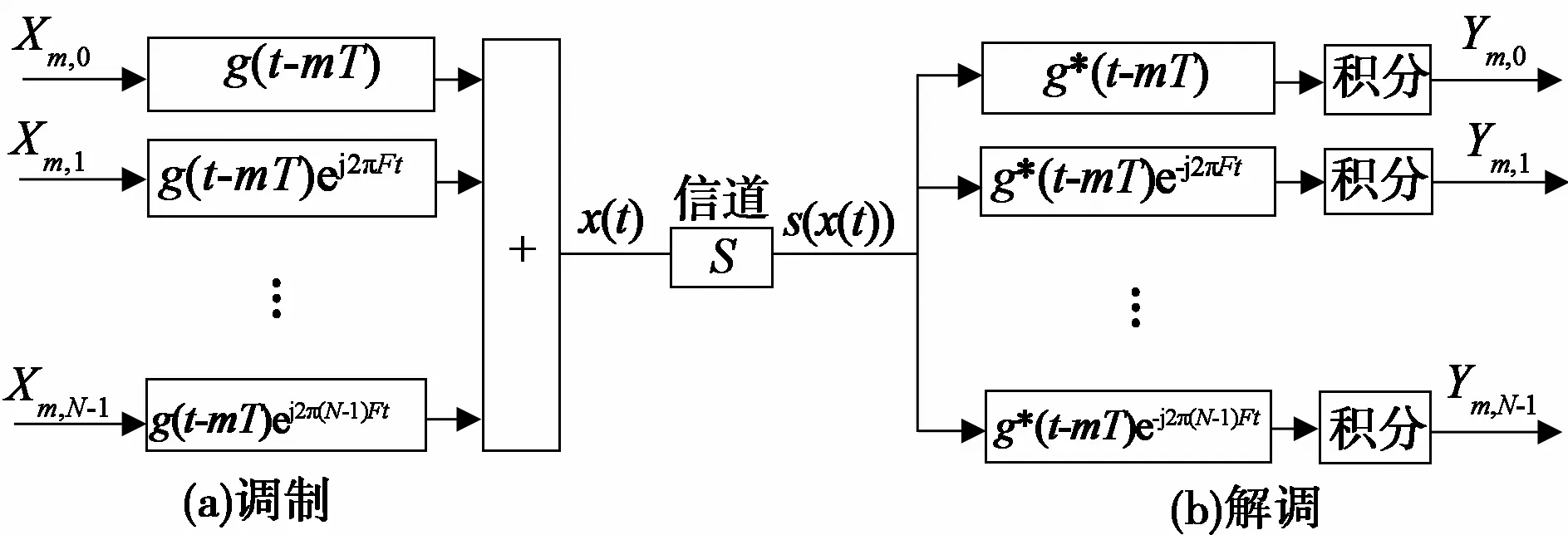
图2 基于Gabor变换的OFDM系统框图Fig.2 OFDM system diagram based on Gabor transform
数据符号Xmn经过子载波调制(即Gabor变换)得到OFDM等效基带信号:
(2)
式中,gmn(t)为Gabor基函数,它是由母函数g(t)的时间移位和频率调制所构成的,其表达式为
gmn(t)=g(t-mT)ej2πnFt
(3)
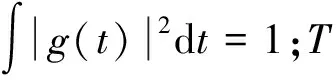
经过时变信道后的接收信号为
(4)
选取广义平稳不相关散射(WSSUS)信道来描述实际信道,则信道扩展函数s(τ,υ)满足[6]

(5)

若忽略噪声的影响,仅考虑信道带来的干扰,接收信号经过子载波解调后得到:
(6)

(7)
系数smnm1n1描述了整个信道特性,经过推导,其表达式为
(8)
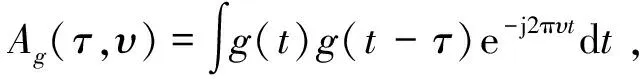
3.2 性能分析
本小节推导系统的信干比并分析系统的性能。将式(7)写成期望信号与干扰(ISI/ICI)之和的形式:
(9)
得到干扰部分能量:
EI=E{ |Ymn-Xmnsmnmn|2}
(10)
期望信号部分能量:
EX=E{ |Xmnsmnmn|2}
(11)
则系统的信干比为
(12)
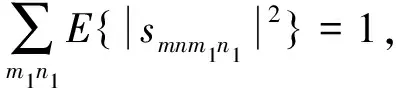
(13)
由式(13)可知,系统的SIR受信道和脉冲性能的影响,当上式分子中的积分式取最大值时,相应的系统SIR可以达到最优。
4 脉冲成形滤波器设计及其对系统性能的影响
本节研究采用高斯脉冲的OFDM系统,并推导出信干比公式及满足最优条件的信干比。
4.1 采用高斯脉冲成形时系统性能分析
定义脉冲g(t)的时间和频率均值分别为
(14)
式中,G(w)为g(t)的傅里叶变换,令:
(15)
式中,Δt为脉冲时宽,Δw为脉冲带宽。ΔtΔw为脉冲的时频扩展,且满足ΔtΔw≥1/2或ΔtΔf≥1/4π,它可以衡量脉冲的时频聚集性,其值越小,脉冲的时频聚集性越好[9]。
设归一化高斯脉冲表达式为
(16)
其自模糊函数为
(17)
将α用脉冲的时宽Δt来表示,即有:
在平坦多径-多普勒信道下,将式(17)代入式(13)中,有:
(18)
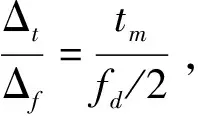
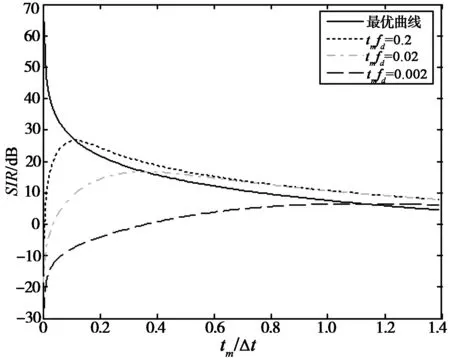
图3 高斯脉冲成形OFDM系统的SIR比较Fig.3 The SIR comparison of Gauss pulse shaping OFDN system
图3给出了式(18)的仿真结果。我们分别固定信道扩展因子tmfd的值为0.2、0.02、0.002,画出了式(18)SIR随相对比例tm/Δt变化的曲线,用虚线表示。由于tm和fd的值没有固定,只固定tmfd的值,所以曲线更能反映出tm和fd取任意值时系统的性能。从这3条曲线可看出信道扩展因子影响系统的SIR性能,它的值越小,其带来的干扰越小,系统性能越好。同样地,我们也给出了式(19)满足最优条件时的SIR仿真结果,用实线表示。从图中可见对不同的信道扩展因子,其SIR的最大值均在这条最优曲线上,这就充分体现了其最优性能。在已知信道最大时延和最大多普勒频移的情况下,通过调整脉冲时宽和带宽满足式(20)来匹配信道特性,此时系统产生的干扰是最小的。
(20)
4.2 仿真及分析
通过仿真分析了平坦多径-多普勒信道和Jakes信道下本文提出的优化高斯脉冲成形OFDM系统的性能,并与采用矩形脉冲的CP-OFDM系统性能进行了比较。
仿真中,OFDM符号周期T′=1/F,循环前缀Tg=0.25T′,令T=T′+Tg,即取TF=1.25。取子载波数N=128,固定归一化最大时延tm的值为0.01,此时这两个系统主要受多普勒频移的影响,比较它们随归一化最大多普勒频移变化的SIR曲线。图4给出了平坦多径-多普勒信道下的SIR曲线,从图中可以看出优化高斯脉冲成形OFDM系统的SIR性能优于CP-OFDM系统,尤其是多普勒频移较大时,其SIR性能改善更明显。当多普勒频移取0.05时其SIR仅改善了5 dB;当多普勒频移取0.5时其SIR可改善15 dB左右。由于固定tm的值,信道产生的ISI不变,优化高斯脉冲成形OFDM系统在减少ISI的同时对ICI的抑制能力比CP-OFDM系统更强。同样地,该方法也适用于Jakes信道模型,如图5所示。

图4 平坦多径多普勒信道下的SIR比较Fig.4 The SIR comparision in flat multipath and Doppler channels
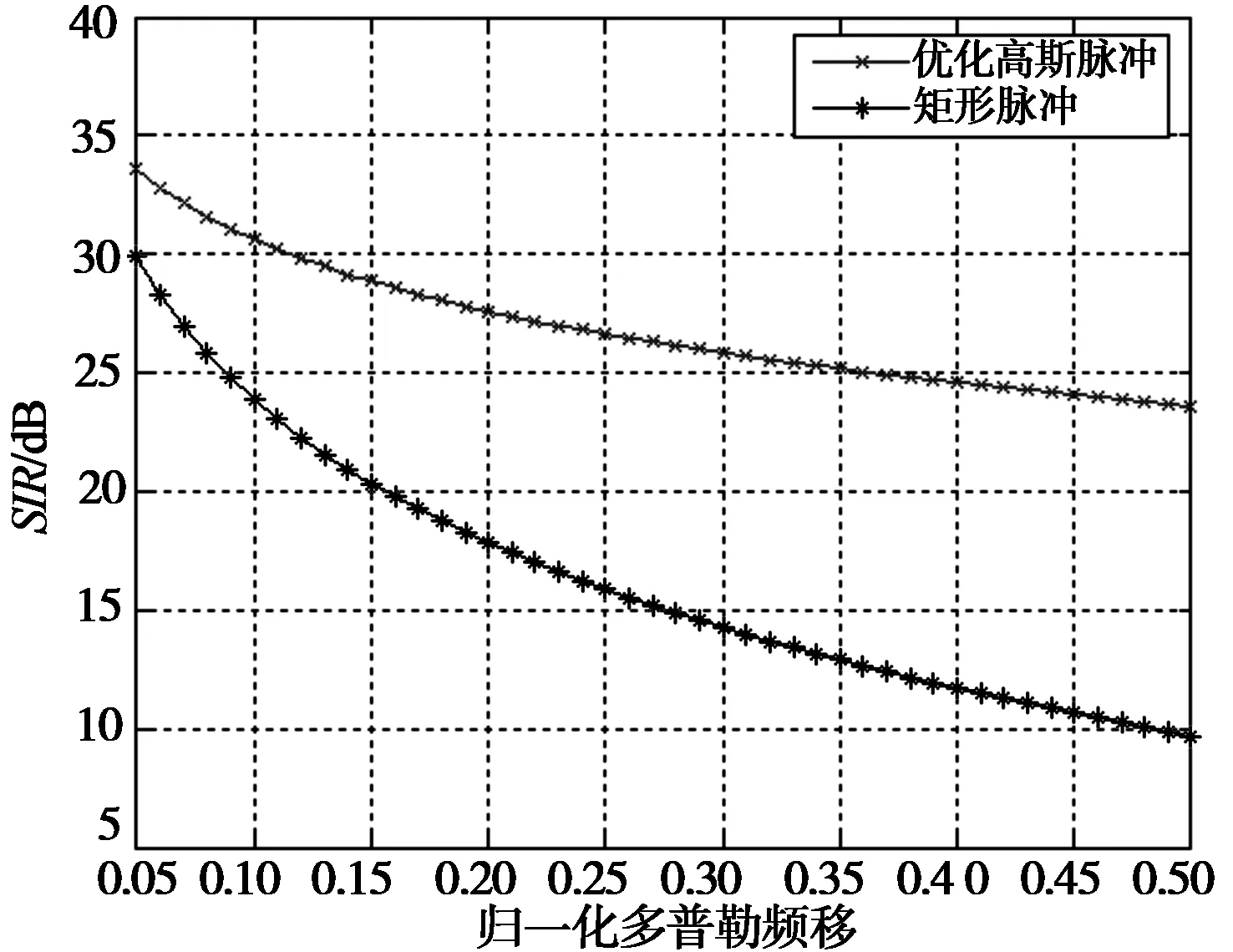
图5 Jakes信道下的SIR比较Fig.5 The SIR comparision in Jakes channels
传统的CP-OFDM系统采用矩形脉冲,可以很好地抵抗信道的时间弥散,但其频域聚集性较差,当多普勒频移存在时,频率弥散使子载波之间的正交性遭到破坏,导致系统性能明显降低。而优化高斯脉冲具有较好的时频域聚集性,可以更好地解决时间弥散和频率弥散信道带来的ISI和ICI,改善OFDM系统性能。
5 结 论
由于OFDM系统对信道频率弥散较为敏感,因此本文提出一种新的OFDM脉冲成形方法,实验结果表明,该方法得到的高斯脉冲是最优的,其系统SIR性能最好。并且同CP-OFDM系统相比,该系统在减少信道时间弥散带来的ISI的同时更好地抑制了频率弥散所带来的ICI,且频率弥散越大,ICI抑制的效果越好,这表明高斯脉冲良好的时频聚集性得到了更好的利用。由于脉冲成形的设计还与时频网格有关,因此如何选择合适的时频网格适应信道特性是尚待需要解决的问题。
参考文献:
[1] Strohmer T,Beaver S. Optimal OFDM design for time-frenquency dispersive channels[J].IEEE Transactions on Communications,2003,51(7):1111-112.
[2] 简伟,沈越泓,李毅.基于广义Gabor变换的最有LOFDM系统的脉冲成形[J].电子与信息学报,2006,28(7):1274-1278.
JIAN Wei,SHEN Yue-hong,LI Yi.Pulse-shaping based on Generalized Gabor Transform for Optimal LOFDM System[J].Journal of Electronics & Information Technology,2006,28(7):1274-1278.(in Chinese)
[3] Bolcskei H,Duhamelb P,Hleissb R.Orthogonali- zation of OFDM/OQAM pulse shaping filters using the discrete Zak transform[J].Signal Processing,2003,83(7):1379-1391.
[4] 陈晖,陈晓光.基于OFDMOQAM系统的时频局域优化脉冲成形滤波器设计[J].电路与系统学报,2006,11(6):86-90.
CHEN Hui,CHEN Xiao-guang.Time-frequency well-localized pulse shaping filter design for OFDM/OQAM system[J].Journal of Circuits and Systems,2006,11(6):86-90.(in Chinese)
[5] Kozek W,Molisch A F.Nonorthogonal pulse-shapes for multicarrier communications in doubly dispersive channels[J].IEEE JSAC,1998,16(8):1579-1589.
[6] Trigui I,Siala M,Affes S,et al.Optimum pulse shaping for OFDM/BFDM systems operating in time varying multi-path channels[J].IEEE GLOBECOM,2007,1(11):3817-3821.
[7] Giannalis G B,等.无线通信与移动通信中信号处理研究的新进展[M].刘郁林,等.译,北京:电子工业出版社,2004.
Giannakis G B,et al.Signal Processing Advances in Wireless and Mobile Communications[M].Translated by LIU Yu-lin,et al.Beijing:Publishing House of Electronics Industry,2004.(in Chinese)
[8] Liu K,Kadous T, Sayeed A M.A signaling frame- work for time-varying multipath fading channels[C]//2002 IEEE 56th Vehicular Technology Conference Proceedings.[S.l.]:IEEE,2002:1864-1868.
[9] Liu K,Kadous T, Sayeed A M.Orthogonal time-frequency signaling over doubly dispersive channels[J].IEEE Transactions on Information Theory,2004,50(11):2583-2603.
