认知无线电中衰落环境下的能量检测性能分析*

(南通大学 电子信息学院，江苏 南通 226019)

1 引 言

近年来，认知无线电(Cognitive Radio，CR)技术已经成为无线通信领域研究的新方向。频谱检测技术作为认知无线电的关键技术之一[1]，也已经成为研究的热点技术之一。目前，基于发射机的频谱检测方法主要有3种，即能量检测[2]、匹配滤波器检测[3]和循环平稳特征检测[4]。其中，匹配滤波器检测需要认知用户了解主用户发射信号的先验知识(如调制方式、脉冲波形等)；循环平稳特征检测依赖高强度的FFT运算，所以计算复杂度高，并且需要较长的观察时间来提取信号的特征信息；相比之下，能量检测具有实现简单、无需额外信息等优点，因此得到广泛的研究和重视。能量检测作为一种简单、直接和有效的检测方法，能够在没有任何先验知识的情况下实现对被检测信号的准确监测[5]。但将信号能量作为检测的唯一参数，必然造成能量检测对接收信噪比的敏感。因此，研究在不同衰落信道条件下能量检测的具体性能具有重要的意义。Urkowitz[6]对带限平坦衰落高斯信道条件下的信号能量检测问题进行了研究和分析。Kostylev[7]在Urkowitz的基础上针对幅度服从Rayleigh、Rice和Nakagami 3种分布的信号检测问题进行了研究，并给出了信号检测概率表达式。值得注意的是，Kostylev的工作均是在模拟域上完成的。文献[8]在数字域上对理想高斯白噪声信道条件下的能量检测性能进行了初步分析，并给出检测概率与接收信噪比和检测数字存储空间之间的关系。文献[9]在Urkowitz[6]的基础上给出了不同衰落条件下的检测性能分析结果。最近，Digham[10]针对衰落信道条件下的能量检测性能做了进一步的研究，给出了慢衰落条件下检测概率的闭解析式，并且提出了两种检测分集策略。本文工作与前人不同的地方在于：给出了分析能量检测性能的一种可选方法，该方法严格按照能量检测器的工作流程，在等效低通数字域上通过严格的数学推导，给出能量检测在典型的慢衰落信道和阴影衰落信道上的检测性能表达式；此外，本文还在统计意义上，给出了小信噪比和大信噪比两种条件下能量检测器的检测概率与观测点数或检测器抽样速率之间的关系。结果表明，能量检测器可以通过适当增加观测点数或提高抽样频率来补偿信噪比的下降。

2 检测模型

图1是能量检测器的基本工作流程。

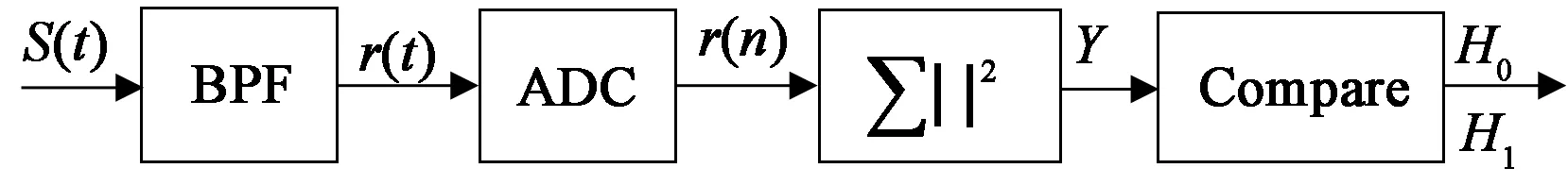
图1 能量检测器工作流程
Fig.1 Working flow of energy detector

能量检测器首先将收到的信号s(t)通过带通滤波器(Band-Pass Filter，BPF)滤除带外噪声，得输出信号r(t)。滤波器的特性可表示为

(1)

滤波器输出信号可表示为

(2)

式中,Zl(t)和Sl(t)分别是等效低通高斯白噪声和被检测信号的等效低通信号；fc为载波频率；H1和H0分别表示存在和不存在被检测信号的两种假设；αejθ是信道衰落因子，在瑞利衰落条件下αejθ服从复高斯分布。假设Zl(t)为功率谱密度为N0的低通复高斯白噪声。r(t)的等效低通信号rl(t)可简化为

(3)

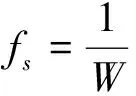
(4)

式中,n=1,2,…,m。

3 检测概率分析

记Y为rl(n)的能量，即:

(5)

(6)

此时，Y可以看做是由N=2m个独立高斯随机变量模的和。因此，Y可看作是维度为N=2m的卡方分布，它们的均值和方差为

(7)

(8)

式中，σ2=N0W。因此，H0和H1条件下Y的概率密度函数f0(y)和f1(y)可以分别由式(9)和式(10)给出：

(9)

(10)

下面将对接收信号能量与判决门限λ进行比较判决。令Pf为在H0条件下接收能量Y>λ的概率，在这里将其称为虚警概率；Pd为在H1条件下接收能量Y>λ的概率，即正确检测的概率，令Pm=1-Pd，即为漏检概率。下面给出Pf、Pm和Pd的数学表达式：

(11)

(12)

Pm=1-Pd

(13)

式中，r为接收信号的信噪比，即:

(14)

(1)瑞利衰落信道

瑞利衰落信道条件下，接收信号的信噪比r服从指数分布，其概率密度函数为

(15)

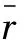
(16)

(17)

(18)

(2)阴影衰落信道

因为阴影衰落信道条件下，接收信号的信噪比r服从对数正态分布，其概率密度函数为

(19)

(20)

(21)

(22)

4 其它参量分析

在上一节中我们将式(6)看作是由N=2m个独立高斯随机变量模的和，因此Y可以用维度为N=2m的卡方分布来逼近。为了发现能量检测中其它变量之间的一些关系，我们重新审视式(6)。由中心极限定理，在H0或H1条件下，当N足够大时，Y可以看做服从高斯分布。式(23)和式(24)分别给出了H0和H1条件下Y的均值和方差：

(23)

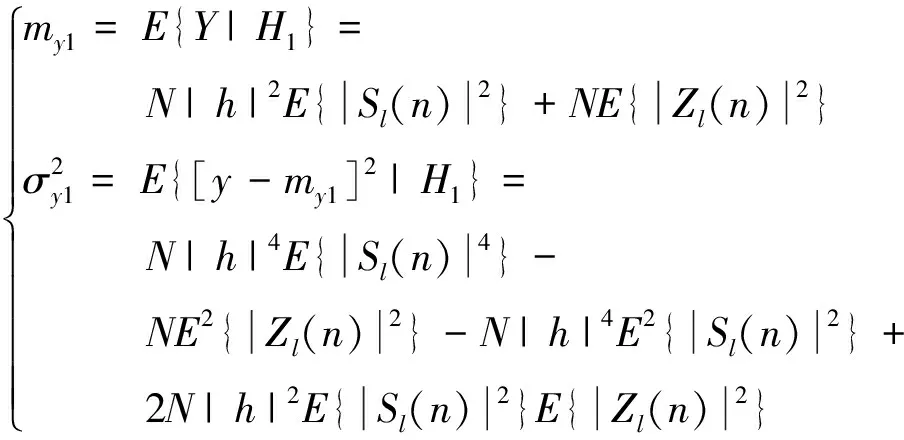
(24)

因此，在H0或H1条件下Y的概率密度函数可以重写为

(25)

(26)

与上一节一样，下面将Y与门限λ进行比较得出Pf和Pm，具体由式(27)和式(28)给出：

(27)

(28)

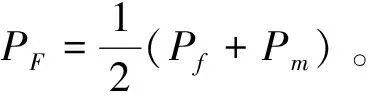
(29)

因此，可得最佳判决门限:

(30)

此时，总误检率为

(31)

其中，

(32)

(33)

式中,α与接收信号的形式有关，r为接收信噪比。

对式(31)进行近似表示可得：

(34)

(35)

由式(34)可以看出，在小信噪比情况下最佳总误检概率与接收信噪比r和观测点数N有关。其中N依赖于观测时间内的观测点数，当观测时间T一定时N与离散化频率fs成正比；或者说在离散化频率fs一定的情况下与观测时间T成正比。

由式(35)可以看出，在大信噪比情况下最佳总误检概率只与N和α有关，与接收信噪比无关。其中N的变化规律上面已说明；而α(见式(32))只与发送信号的形式有关。在复信号情况下，当发送信号为高斯信号时α=2，当发送信号为幅相调制信号时(如：PSK、QAM等)α=1，其它信号形式α介于1～2之间[8]。因此，从能量检测角度来讲，提高N或减小α均可以提高检测性能。

为了得出在不同信道条件下，最佳总误检概率的表达式，还需要将式(31)在不同衰落信道条件下对接收信噪比求统计平均，即将式(31)在式(15)和式(19)下求统计平均。这里我们不具体给出不同衰落条件下的PF，而是重点考察不同信道条件下，PF与N和r之间的关系。

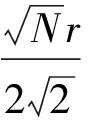
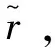
5 数值结果与分析

图2给出瑞利衰落信道条件下，虚警概率与漏检概率之间的关系(图中σ=1)。由图2可以看出，衰落信道条件下，随着平均信噪比的下降检测性能均下降。在大信噪比情况下，即SNR=12 dB时，虚警概率在0.1的时候，漏检概率已在0.18左右。因此瑞利衰落条件下，能量检测需要较大的平均信噪比。

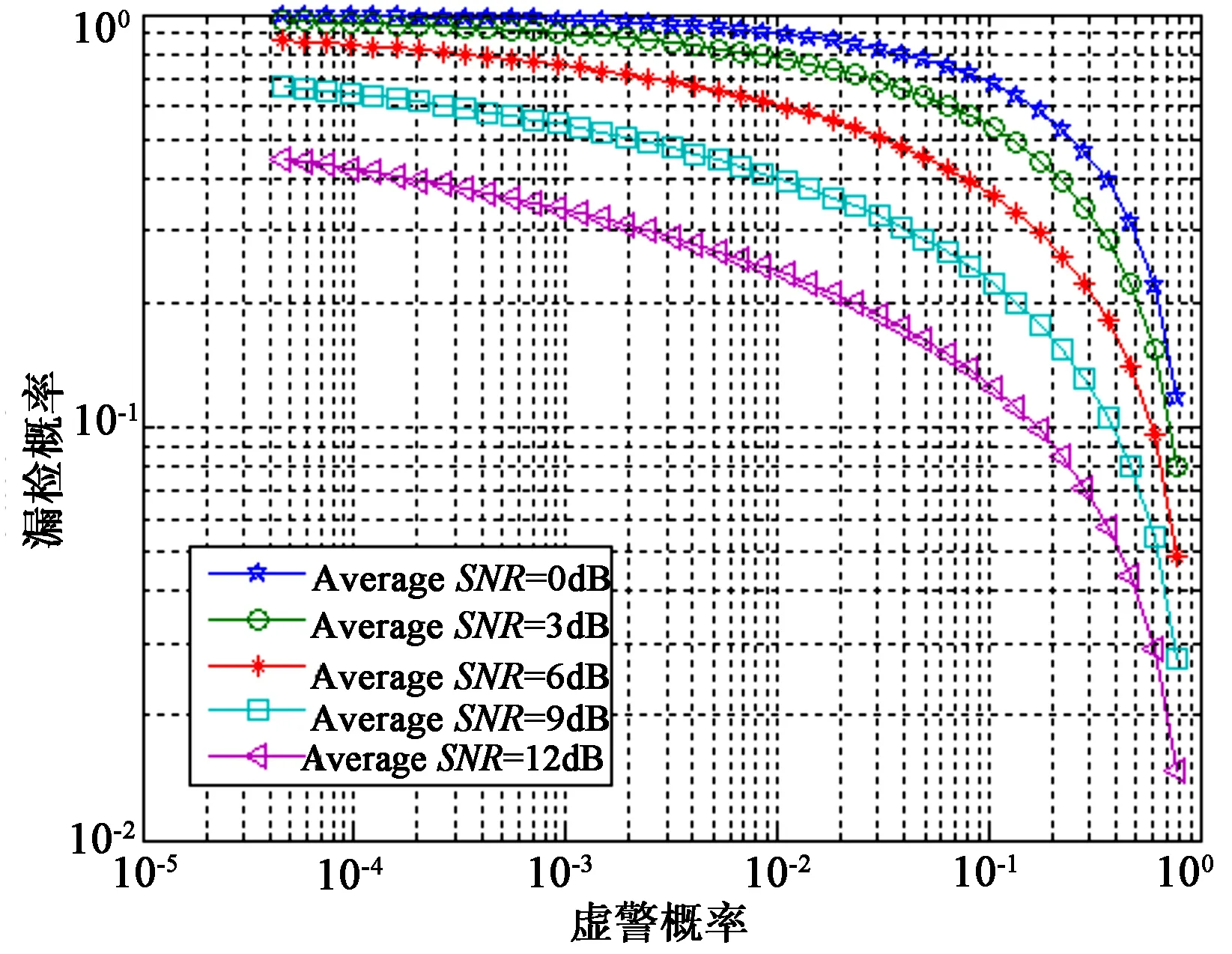
图2 瑞利衰落环境下能量检测性能Fig.2 Detection performance in Rayleigh fading channel

图3给出不同σs取值的阴影衰落下的(图3中σ=1，μs=0)虚警概率与漏检概率之间的关系。由图3可以看出，当σs=3 dB时，阴影衰落环境下漏检测概率大部分大于0.5，也就是检测出主用户的概率小于0.5。因此在阴影衰落坏境下，单独的能量检测性能稳定性很差。

图3 阴影衰落环境下能量检测性能Fig.3 Detection performance under shadow fading

图4给出高斯噪声条件下，接收信噪比r与观测点数N之间的关系。由图4可以看出，在接收信噪比一定情况下，随着检测性能要求的提高，观察点数N呈平方增长。也就是说，当观测时间T一定时要求离散化频率fs呈平方增长，或在离散化频率fs一定的情况下观测时间T呈平方增长。

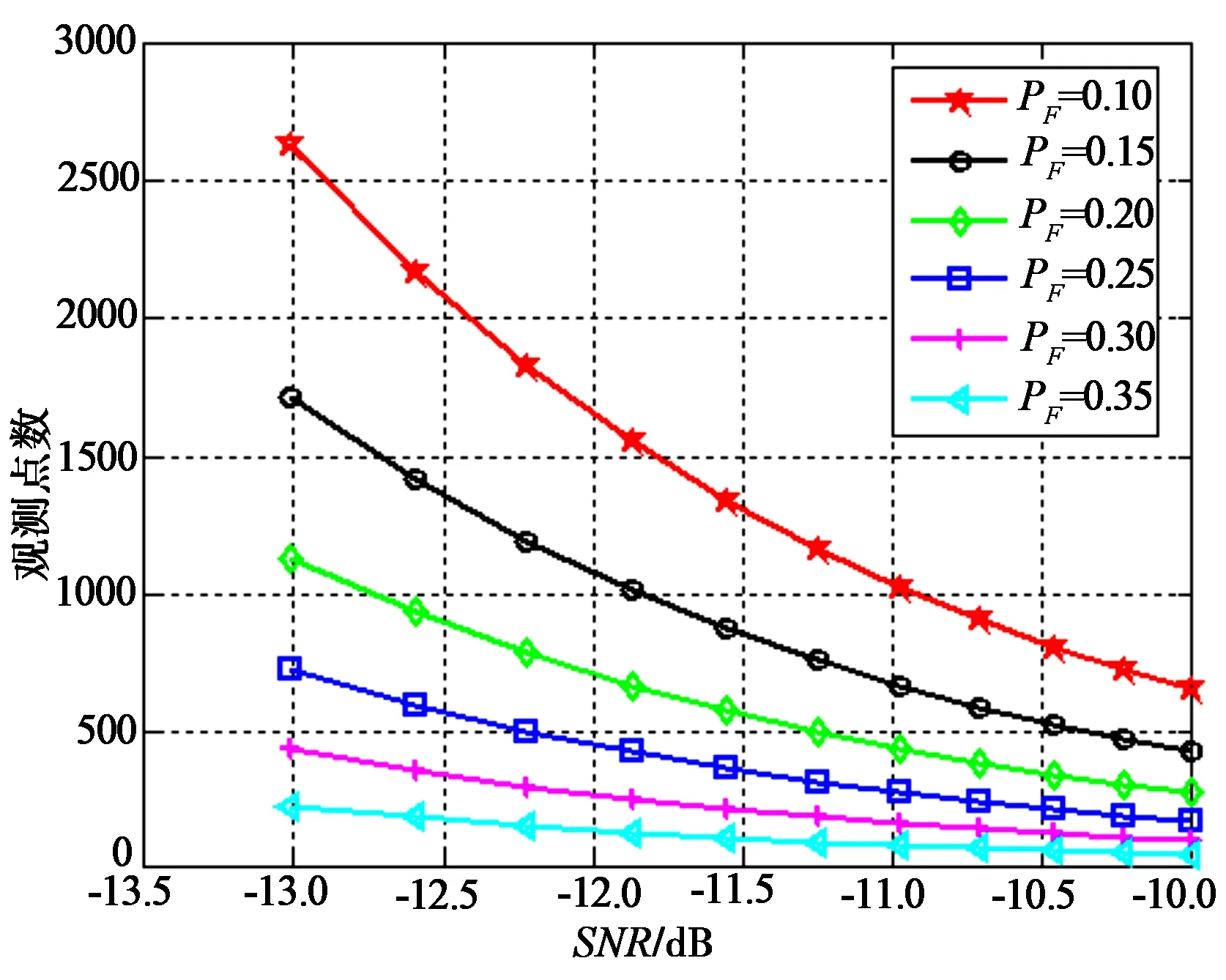
图4 高斯信道下观测点数与信噪比的关系Fig.4 Observation points under different SNRs in additive white Gaussian noise channel

图5给出衰落条件下观测点数与信噪比之间的关系。由图4和图5可以看出，在相同检测性能条件下，衰落信道要求更多的观测点数。也就是说，当观测时间T一定时要求离散化频率fs更高，或在离散化频率fs一定的情况下观测时间T更长。

图5 衰落信道下观测点数与信噪比的关系Fig.5 Observation points under different SNRs in fading channel

图6给出深度衰落与非衰落信道条件下，接收信噪比r与观测点数N之间的关系。可以看出，在相同的检测性能要求下，深度衰落信道(衰落因子β=0.3)要求的观测点数大约比非衰落信道要求的多10 dB。

图6 不同信道下观测点数与信噪比之间的比较Fig.6 Observation points under different SNRs and different channels

6 结 论

本文在等效低通数字域上通过严格的数学推导，给出了能量检测在典型的慢衰落信道和阴影衰落信道上的检测性能表达式。同时，在统计意义上对能量检测器的检测概率与观测点数或检测器工作速率之间的关系进行了分析。结果表明，能量检测的性能对接收信噪比比较敏感，在瑞利衰落信道条件下检测性能明显下降；在阴影衰落环境下能量检测性能恶化严重，当σs=3 dB时阴影衰落环境下漏检测概率大部分情况下已经大于0.5，此时能量检测将失效。此外，研究还发现，可以通过适当增加观测点数或提高离散化频率来补偿能量检测时信噪比的下降，但在深度衰落条件下(衰落因子β=0.3)，要保持检测性能，要求的观测点数大约比非衰落信道要求的多10 dB。

参考文献：

[1] Haykin S.Cognitive radio: Brain-empowered wireless commmnications[J].IEEE Journal on Selected Areas in Communications, 2005,23(2):201-220.

[2] Kolodzy P J.Interference temperature: a metric for dynamic spectrum utilization[J].International Journal of Network Management,2006,16 (2):103-113.

[3] Sahai A, Hoven N, Tandra R. Some fundamental limits on cognitive radio[C] // Proceedings of Forty-second Allerton Conference on Communication, Control, and Computing. Monticello, USA：[s.n.], 2004: 772-776.

[4] Cabric D,Mishra S M,Brodersen R W.Implementation Issues in Spectrum Sensing for Cognitive Radios [C] // Conference Record of the Thirty-Eighth Asilomar Conference on Signals,System and Computers.Pacific Grove,USA：[s.n.],2004:772-776.

[5] Letaief K B. Cooperative Communications for Cognitive Radio Networks[J]. IEEE Proceedings, 2009, 97 (5): 878-893.

[6] Urkowitz H.Energy Detection of Nnknown Deterministic Signals[J].IEEE Proceedings,1967,55(4):523-531.

[7] Kostylev V I.Energy Detection of a Signal with Random Amplitude[C]//Proceedings of IEEE International Conference on Communications.NewYork,USA:IEEE,2002:1606-1610.

[8] Tang H.Some Physical Layer Issues of Wide-band Cognitive Radio Systems[C]//Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks.Baltimore,USA:IEEE,2005:151-159.

[9] Digham F F Alouini M S,Simon M K.On the Energy Detection of Unknown Signals over Fading Channels[C]//Proceedings of IEEE International Conference on communications.Anchorage,USA:IEEE,2003:3575-3579.

[10] Digham F F,Alouini M S,Simon M K.On the Energy Detection of Nnknown Signals over Fading Channels[J].IEEE Transactions on Communications,2007,55(1):21-24.

[11] Proakis J G.Digital Communications[M].New York:McGraw Hill,2001:38-44.