改进的SLFM宽带DOA估计方法*

(海军工程大学 电子工程学院，武汉 430033)

1 引 言

波达方向(DOA)估计是阵列信号处理的一个重要方向，根据信号带宽，可将DOA估计问题分作窄带与宽带两大类。目前，窄带信号的DOA估计算法已经非常成熟，包括数字波束形成(DBF)、MUSIC、ESPRIT等[1]。与窄带信号相比，宽带信号的能量不集中于一个与载频相比较小的频段内，阵列的输出无法通过某一频率分量进行量化，因此宽带的DOA估计算法与窄带存在较大不同。ISSM(Incoherent Signal Subspace Method)是最简单的宽带方法[2]，通过滤波器组将宽带信号变成一组窄带信号，运用窄带方法得到DOA的估计，当信噪比非常大时，该方法精度最高，但ISSM没有利用宽带信号不同频率成分之间的关系，因此在中小信噪比环境下，性能很不理想。相干信号子空间方法(CSSM)[2]利用聚焦方法将宽带能量集中，克服了ISSM的缺点，在小信噪比环境中，性能最好，但需要对DOA进行预估，否则性能急剧下降。WAVES[2]的原理与CSSM相似，不需要进行DOA预估，计算量因而得以改善，但所能达到的估计精度不如CSSM。TOPS[2,3]与ISSM一样，亦属于不相干类方法，其性能介于ISSM与CSSM之间，在信噪比适中时，最为理想。以上诸方法在形式上虽各有不同，但都利用信号的相位信息估计DOA，因此其阵元间隔不宜超过半波长，适合小孔径阵列[4]。

除了相位，还可以利用时间信息对DOA进行估计，使阵元间隔突破半波限制，这类算法包括基于时延估计的两步定位方法(下文简称两步法)、联合可控响应功率和相位变换(SRP-PHAT)等。两步法[5]先估计宽带信号达到不同阵元的时间延迟，然后优选时延估计DOA，该方法计算量相对较小，缺点是只能工作于单信号环境。SRP-PHAT[6,7]先计算阵元对之间的广义互相关(GCC)，然后利用GCC进行空间搜索，根据峰值计算DOA的估计，其优点是适用于多信号环境，但计算量巨大。近来，又出现了信源线拟合算法(SLFM)[4,8]，该方法计算量小，适用于多信号环境，但均匀线性阵列(ULA)的要求限制了其使用。本文针对SLFM的缺陷，对其加以改进，提出了通用型SLFM(GSLFM)。新方法运用曲线-直线变换，使SLFM突破ULA的限制，适用范围扩展到非均匀线性阵列(NLA)，计算机仿真实验结果表明,GSLFM能够在NLA条件下工作，其性能与SLFM基本相当。

2 信号模型

考虑由M个阵元组成的均匀线性阵列，在远场区，有P个互不相关的宽带信号。若以第1个阵元作为参考阵元，则第m个阵元接收到的信号形式可表示为

(1)

式中，m=1,2,…,M,Am,p是阵元m对第p个宽带信号的增益，sp(t)是宽带信号p的表达式，nm(t)是阵元中的加性噪声，τm,p=dmsinθp/c表示信号到达第m个阵元相对于参考阵元的时延，dm表示第m个阵元相对于参考阵元的距离，θp表示第p个信号的到达角，c是波的传输速度。为讨论方便，本文将Am,p设置为1。

计算xm(t)与x1(t)的互相关函数，记作rm(t)，有:

(2)

式中，T表示接收信号的持续时间。因为宽带信号之间互不相关，所以在rm(t)中会出现P个峰值[4]。将宽带信号p对应的峰值时间记作tm,p，则满足:

tm,p=τ1,p-τm,p

(3)

根据式(3)，在ULA条件下，序列t1,p，t2,p，…，tM,p应为等差序列。对rm(t)进行采样，将产生一个M×(2N-1)维矩阵R：

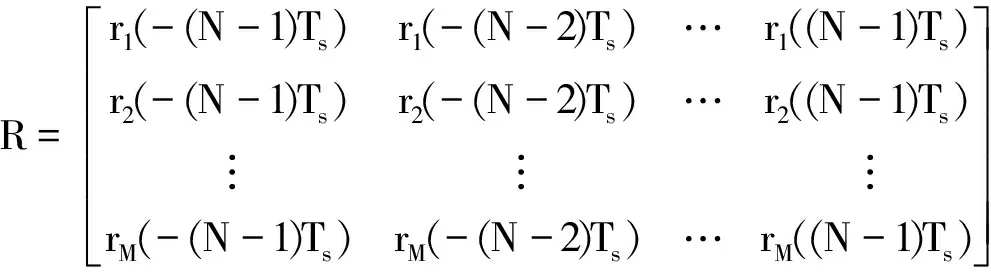
(4)

式中，Ts为采样间隔时间，满足T=(N-1)Ts，N为一整数。若将R中的元素看作像素，则R可被表示成一幅二维灰度图像，如图1所示。由于t1,p，t2,p，…，tM,p为等差序列，在图像R中，该序列会对应一条直线，这条直线在文献[4]中被称作信源线(Source Line,SL)。又由于每个宽带信号都会对应一组等差序列，因而图像中的信源线数量与信号数量相同。矩阵R被称作信源线矩阵(SL Matrix,SLM)。

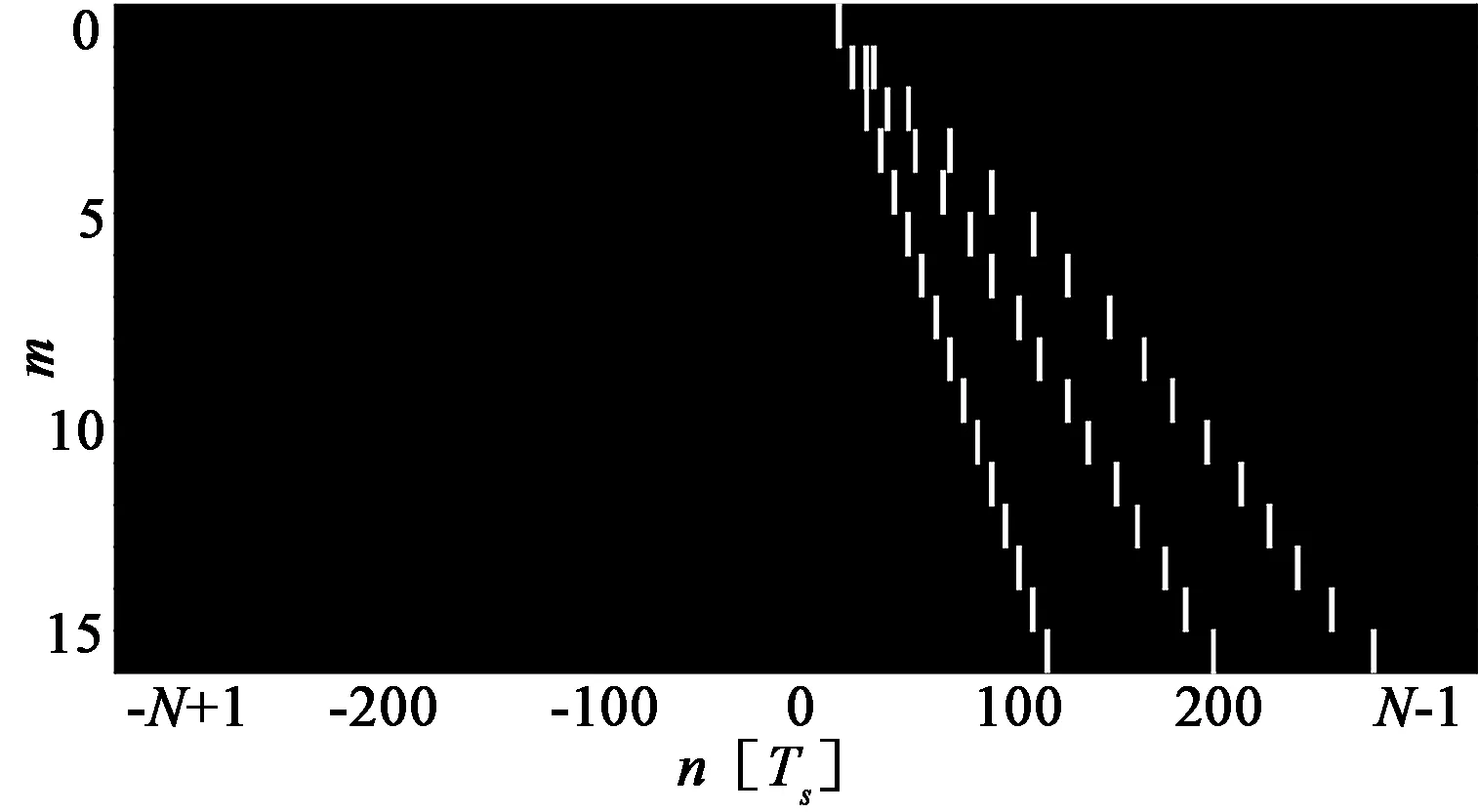
图1 环境中存在3个宽带信号，每个信号对应一条信源线Fig.1 There are 3 wideband sources in far-field, each of which corresponds to a source line

宽带信号与信源线一一对应，而信源线倾斜角与DOA一一对应，因此可以通过估计倾斜角来估计DOA，方程(5)建立了两者之间的关系:

(5)

式中，αp为第p个信号对应的信源线的倾斜角。这样，DOA估计问题就转变成信源线倾斜角的估计问题。而倾斜角估计属于图像处理中的直线拟合(Line Fitting)范畴，目前算法较多，文献[4]选取了矩阵束(MP)方法求解倾斜角。

3 NLA条件下的SLFM方法

ULA是SLFM的前提条件，也是其缺陷，本节将对SLFM进行改进，使之能够适用于NLA。对于ULA，序列t1,p，t2,p，…，tM,p为等差序列，因而R中的信源线为直线。而对于NLA，序列t1,p，t2,p，…，tM,p不再等差，信源线也就不再是直线，如图2所示。不同的DOA对应不同形状的信源曲线，因而很难如直线一样确定其倾斜角，也就不能直接运用SLFM。但如果能通过变换的方式将信源线由曲线变为直线，则SLFM就能够被扩展到NLA。

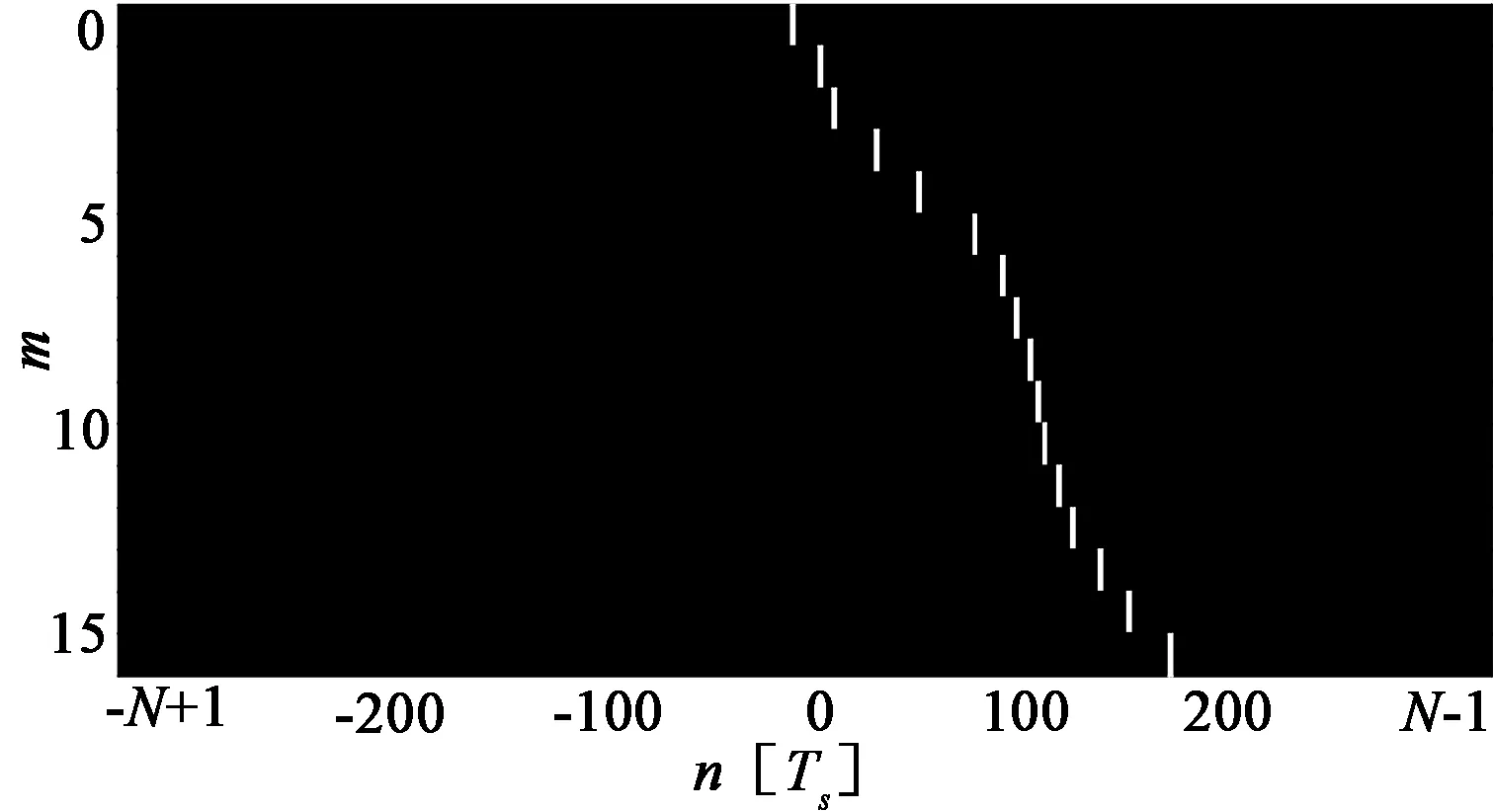
图2 对于NLA，信源线为曲线，而不是直线Fig.2 For NLA，the source line is not straight

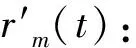
(6)

式中，Δd可以选择不同值，如需保持变换前后阵列孔径不变，Δd应满足式(7)：

(7)

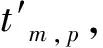
(8)

将τm,p=dmsinθp/c代入式(8)，得到:

(9)

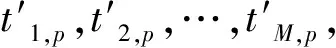
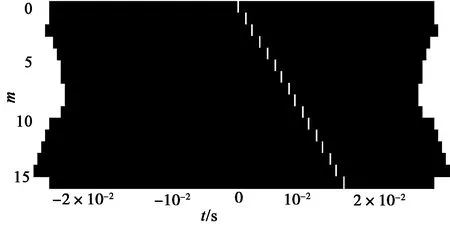
图3 经过曲线-直线变换，图2中的曲线变成直线Fig.3 By transformation,the source curve in figure 2is replaced with the straight line

以上方法似乎可以解决问题，但却存在一个难点：在采样之前必须完成式(6)的计算，然而式(6)要求对接收信号在时间域进行压缩或扩展，势必导致设备量大幅增加。方程(6)固然可以实现曲线-直线变换，但并不最优，可以考虑将变换放入到直线拟合处理当中。

文献[4]采用MP方法求解信源线的倾斜角，该方法需要定义向量z=[z(1),z(2),…,z(M)]T，其中各元素的定义由式(10)给出：

(10)

式中，μ是一个需要适当选择的常量，rm(n)为式(4)中矩阵R的元素。将z(m)中第p个宽带信号对应的成分定义为zp(m)，则有:

(11)

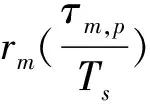
(12)

相应地，zp(m)需要用式(13)表示：

(13)

重新观察序列zp(1),zp(2),…,zp(M)，此时该序列等比，说明式(12)中包含了曲线-直线变换，可以用其取代方程(6)。

为了区别原有的SLFM，本文将改进后的方法称作通用型SLFM(GSLFM)。现将GSLFM算法步骤总结如下：

(1)根据式(1)～(4)，构造信源线矩阵R；

(2)根据式(12)定义向量z=[z(1),z(2),…,z(M)]T；

(3)在步骤2的基础上，运用MP方法估计信源线倾斜角；

(4)根据倾斜角，计算式(5)得到宽带信号DOA的估计。

4 计算机仿真

为了验证GSLFM是否有效，本节在不同实验条件下对GSLFM、SLFM与SRP-PHAT 3种算法进行仿真对比。GSLFM与SRP-PHAT采用非均匀线性阵列，SLFM采用均匀线性阵列，两种阵列的阵元数量与阵列孔径均相同，孔径缺省值为10λ(M-1)，其中M为阵元数量，λ为中心波长。GSLFM与SLFM中的参数μ设为1/16。每组实验进行500次蒙特卡洛仿真，采用均方根误差(RMSE)作为评价指标，对于NLA，每次实验采用不同的阵列流形，由随机函数生成。

4.1 实验1

考察单信号环境中，3种算法在不同信噪比条件下的表现。线性调频脉冲信号起始频率为0.1 MHz，终止频率为1.5 MHz，接收机采样频率为为4 MHz，信噪比测试范围为-10～20 dB，步长为1 dB。在0°～60°之间随机选取50个DOA值，统计得到平均RMSE，如图4所示。

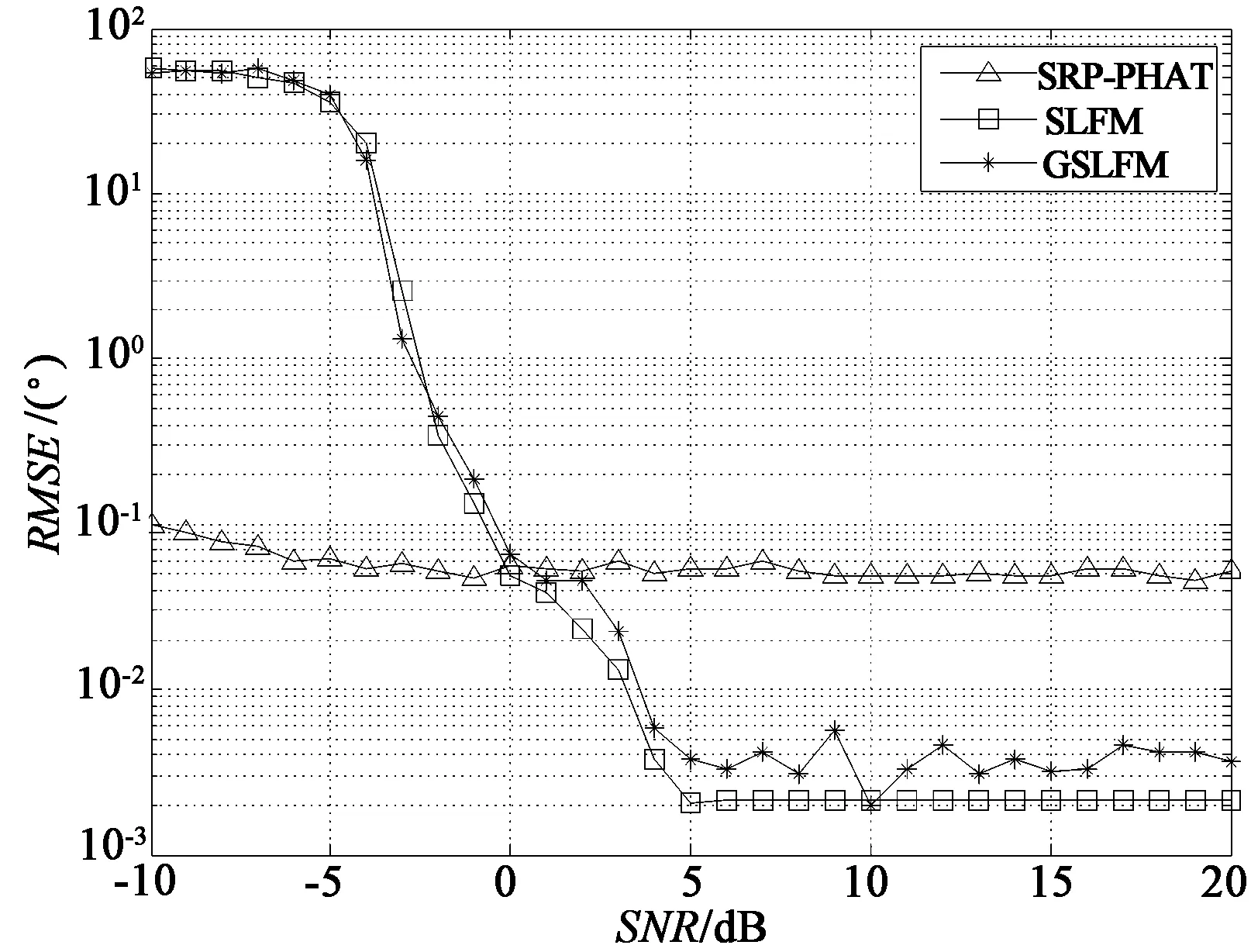
图4 不同信噪比条件下的平均RMSEFig.4 Average value of RMSE for various SNRs

从图4可以看出，在低信噪比区域，SRP-PHAT明显优于另外两种算法。究其原因：SRP-PHAT采取峰值搜索的方式，具有非常好的稳健性，而GSLFM与SLFM通过方程求解，对方程的条件比较敏感，稳健性不如SRP-PHAT。但在高信噪比区域，GSLFM与SLFM表现出较高的估计精度，求根算法发挥了优势。对比GSLFM与SLFM，前者性能接近后者，说明前者成功地将后者的适用范围从ULA扩展到NLA。需要指出的是：采样过程带入了时间量化误差，即峰值只能出现在近似时间点，对于NLA，曲线-直线变换会改变时间量化误差的分布，使其与ULA不同，因而GSLFM的性能较SLFM稍差。

4.2 实验2

考察单信号环境中，3种算法在不同阵列孔径条件下的表现。信噪比为10 dB，对于NLA，相邻阵元间的间隔不同，只能设置平均阵元间隔，依次选择0.5λ，λ，2λ，…，10λ，对应的阵列孔径为0.5λ(M-1)，λ(M-1)，2λ(M-1)，…，10λ(M-1)，其它参数与实验1保持一致。图5给出了在不同平均阵元间隔条件下50个测试DOA的平均RMSE。

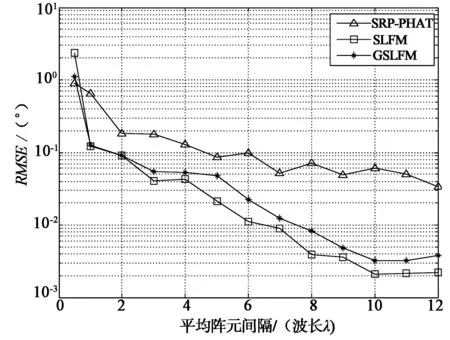
图5 不同平均阵元间隔条件下的平均RMSEFig.5 RMSE for various mean values of aperture

由图5可以看出，当平均间隔为半波长时，3种算法的性能均不理想；随着平均阵元间隔的增大，3种算法的性能均有所改善，原因是增大平均阵元间距相当于降低了时间量化噪声对时延数据的影响，也说明这类利用时间信息求解DOA问题的算法适合大间距环境，如MIMO等系统。当平均间隔较大时，虽然3种算法的估计精度都有所提高，但GSLFM与SLFM提高的程度要好于SRP-PHAT，原因在于前两者算法的本质是最小二乘法，而SRP-PHAT的谱是由若干数据相加得到的，最小二乘法对于时延数据的准确性较后者要更加敏感。

4.3 实验3

考察双信号环境中，3种算法在不同信噪比条件下的表现。信噪比测试范围为-10～20 dB，步长为1 dB。信号1为随机过程，起始频率为0.1 MHz，终止频率为1.5 MHz，设置在23.12°位置，接收机采样频率为4 MHz。信号2为线性调频脉冲，起始频率为0.1 MHz，终止频率1.5 MHz，在0°～60°之间随机选取50次DOA值，统计得到信号2的平均RMSE，如图6所示。从实验结果可以发现，在所有信噪比区域，SRP-PHAT的性能较为均衡，变化不大，稳健性强，尤其在低信噪比区，明显好于另外两种算法。在高信噪比区域，SLFM的性能依然最好，GSLFM与SRP-PHAT基本相当。对比图6与图4还可以发现，在多信号环境中，GSLFM与SLFM的估计性能有所降低，这也是求根算法对方程的条件比较敏感所致。

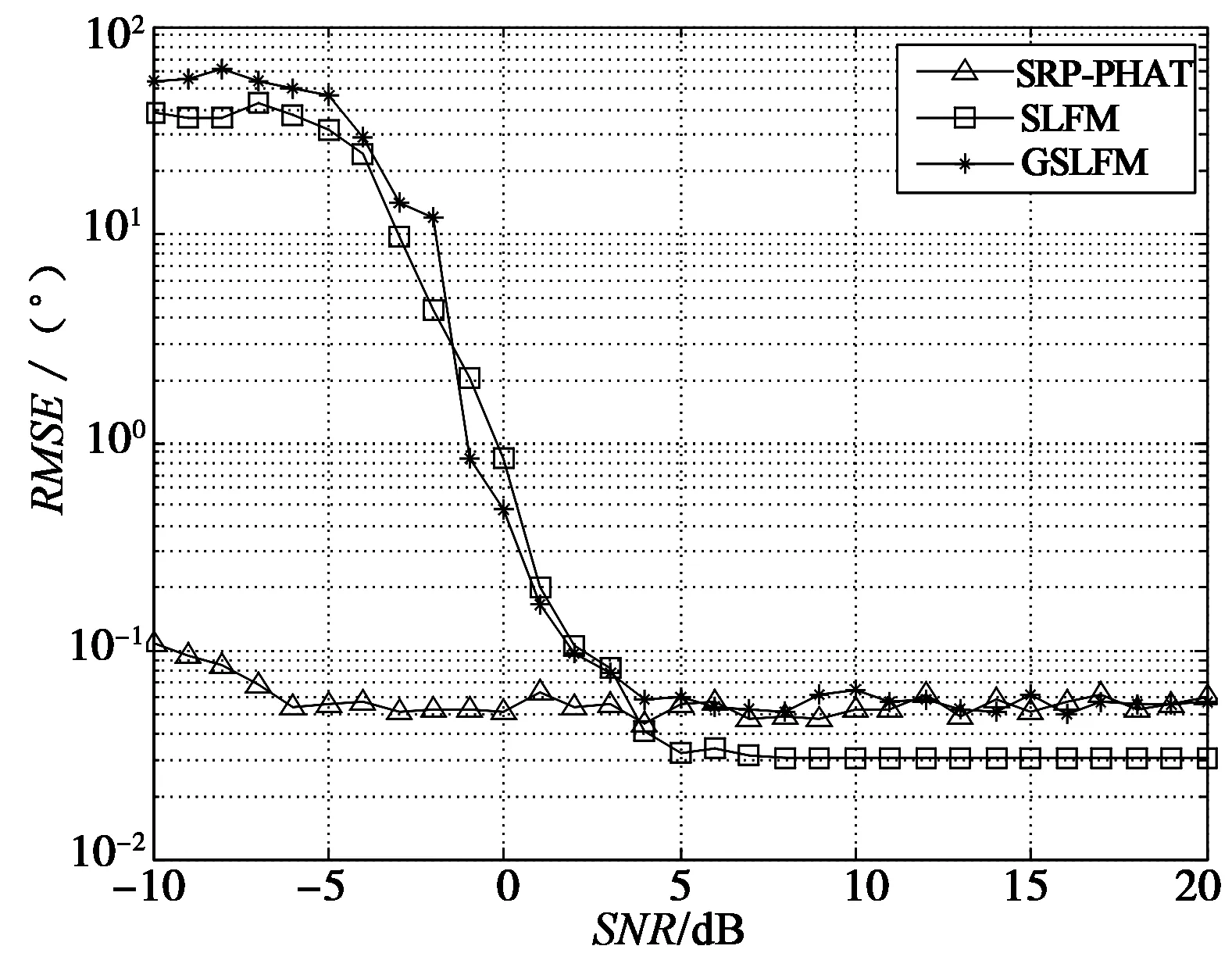
图6 多信号环境中，不同信噪比条件下的平均RMSEFig.6 For scenario of multi-sources, average value of RMSE for various SNRs

5 小 结

为了扩大SLFM算法的适用范围，本文对其进行改进，提出了GSLFM算法，运用曲线-直线变换，将非均匀线性阵列变换成均匀线性阵列。从计算机仿真结果来看，GSLFM在保持原算法估计精度的同时，突破了均匀线性阵列条件的限制。由于曲线-直线变换导致时间量化噪声的分布发生变化，对算法造成一定影响，使得GSLFM的RMSE比SLFM稍高，但差距不明显。与SRP-PHAT算法相比，GSLFM与SLFM更加适合单信源、中高信噪比环境。在今后的工作中，将研究更好的直线拟合方法以提高算法的稳健性和精度。

参考文献：

[1] 张贤达.现代信号处理[M].2版.北京:清华大学出版社,2002:115-150.

ZHANG Xian-da. Modern signal processing[M].2nd ed.Bejing:Tsinghua University Press,2002:115-150.(in Chinese)

[2] SATHISH CHANDRAN. Advances in direction-of-arrival estimation[M]. London: Artech House,2005:49-68.

[3] YEO SUN YOON, LANCE M KAPLAN, JAMES H MCCLELLAN. TOPS: new DOA estimator for wideband signals[J]. IEEE Transaction on Signal Processing,2006,54(6):1977-1988.

[4] ZUO WEI,GAO JUN.SLFM: a new DOA estimator for wideband signals[C]//Proceedings of the 9 th IEEE International Conference on Electronic Measurement & Instruments.Beijing:IEEE,2009:107-111.

[5] PIRINEN, T W YLI-HIETANEN, J PERTILA,et al.Detection and compensation of sensor malfunction in time delay based direction of arrival estimation[C]// Proceedings of the 2004 International Symposium on Circuits and Systems. Piscataway,NJ,USA:IEEE,2004:872-875.

[6] DIBIASE J. A high-accuracy, low-latency technique for talker localization in reverberant environments[D].Rode Island, USA:Brown University,2000.

[7] 谭颖,殷福亮,李细林.改进的SRP-PHAT声源定位方法[J].电子与信息学报,2006,28(7):1223-1227.

TAN Ying,YIN Fu-liang,LI Xi-lin.Sound localization method using modified SRP-PHAT algorithm[J].Journal of Electronics & Information Technology,2006,28(7):1223-1227.(in Chinese)

[8] XIE Peng,LUO Tao,LI Jian-feng,et al.Improved estimator for wideband sources using two references[C]//Proceedings of 2009 IEEE International Conference on Communications Technology and Applications.Beijing:IEEE,2009:10-18.