基于BP神经网络的投资决策阶段可行性预测

韩莎莎

（福建工程学院工程管理系，福建福州350108）

基于BP神经网络的投资决策阶段可行性预测

韩莎莎

（福建工程学院工程管理系，福建福州350108）

众所周知，工程造价估算在项目管理中十分重要，对项目计划管理、费用管理、投标竞标、投资和筹资都有重要作用.它是工程项目可行性研究的基础，也是日后施工阶段造价管理的参考依据.其准确与否直接影响项目的投资决策，它是利用已建类似工程的造价资料和市场变化的信息，对拟建工程投资费用所做的一种预先估计或预测.

投资决策；造价预测；神经网络；可行性预测

神经网络[4]具有优良的非线性特性，非常适合于造价预测的研究，BP神经网络[5，6]具有很强的非线性影射能力，从而具有很好的曲线拟合能力、优化能力和模式分类能力.因此，人工神经网络技术对投资决策阶段的可行性预测有很强的预测能力.

1 投资决策阶段的可行性预测

从甲方的角度来看，投资决策的正确与否十分重要.因此，作为甲方，应该在工程项目投资之前，做好充分地可行性预测，将投资风险尽可能地降到最低.

2 投资决策阶段可行性预测的主要内容

可行性研究是计算、分析、评价各种项目、技术方案和生产经营决策的经济效果的一种科学方法，是技术经济分析论证的一种重要手段[1].这种方法是在运用多种学科成果的基础上形成的，通过对技术方案或建设项目各方面关系的研究分析，从而预测方案或项目所能获得的经济效果.由此可见，可行性研究是项目在投资前期，对拟建项目进行的全面、系统的技术经济等多方面分析与论证，从而为项目投资决策提供重要依据，也为下一阶段开展项目评估打下了基础.

在项目建设中会面临投资方案的比较和选择问题，有时会面临多个方案的比选，评价.因此应采用科学的方法进行评价，合理确定投资方案.投资方案经济效益评价可分为两个基本内容：单方案检验与多方案的比选.单方案检验是指对某个初步选定的投资方案，根据项目收益与费用的情况，通过计算其经济评价指标，确定项目的可行性.单方案检验的方法比较简单，主要步骤如下[2，3]：

（1）确定项目的现金流量情况，编制项目现金流量表或绘制现金流量图.

（2）根据公式计算项目的经济评价指标，如NPV、NAV等.

（3）根据计算出的指标值及相对应的判别准则，如NPV≥0，NAV≥0等来确定项目的可行性.

多方案的比选是指对根据实际情况所提出的多个备选方案，通过选择适当的经济评价方法与指标，来对各个方案的经济效益进行比较，最终选择出具有最佳投资效果的方案.

3 投资决策阶段可行性预测的意义

在工程项目的整个建设过程中，投资决策阶段是进行造价控制的重点阶段，也是风险最大的阶段.因此，做好投资决策阶段的可行性预测对整个工程项目有着十分重大的意义.

工程项目投资具有价值大、投资回收期长、风险大等特点，所以进行工程项目可行性的预测和决策分析是十分重要的.工程项目投资预测具有预见性、明确性、相对性、客观性、可检验性以及灵活性等特点.预测分析可以反复进行，其信息对决策具有指导性作用.工程项目投资成败的关键还在于决策，决策的基础是科学的预测，预测为决策提供直接的服务；但是预测不能代替决策，毕竟只有决策的结果才是直接支配未来的行动方案.工程项目在投资阶段的可行性预测时，必须遵守合法性、合理性、责任性、民主性、科学性以及效益性原则，依照决策分析程序，选择合适的决策方法.工程项目投资的可行性预测和决策是一个动态的过程，它贯穿于项目投资建设活动的始终，根据市场状况以及工程项目的类型、性质和进展情况适时地作出正确的预测和决策分析，就可以保证整个投资活动有序、高效地进行，并取得预期的效果，达到投资的目的.

4 投资决策阶段的可行性预测实例

项目可行性预测的背景资料[7]

背景：（1）某建设项目建设期为2年，运营期为10年.

（2）项目固定资产投资估算总额为5400万元，其中：预计形成固定资产4590万元(含建设期贷款利息为90万元)，无形资产810万元.固定资产使用年限为15年，残值率为6%，固定资产余值在项目运营期末收回.

（3）无形资产在运营期10年中，均匀摊入成本.

（4）流动资金为1000万元，在项目的生命周期期末收回.

（5）项目的设计生产能力为年产量280万件，产品售价为21元/件，销售税金及附加的税率为6%，所得税率为25%，行业基准收益率为8%.

（6）项目的资金投入、收益、成本等基础数据，见表1.

（7）还款方式为在运营期10年之中，按照每年等额本金偿还法进行偿还(即从第3年至第12年).长期贷款利率为7.2%(按年计息)；流动资金贷款利率为5.6%(按年计息).

（8）行业的投资利润率为20%，投资利税率为25%.

表1 某建设项目资金投入、收益及成本表

引入BP神经网络

通过对以上具体工程资料的分析，本文将引入BP神经网络，并且从财务评价的角度分析判断该项目的可行性.

首先，确定BP神经网络的输入信息——这里假定在投资决策阶段其他影响造价的因素均不变，而只有销售税金及附加的税率在变化.即假定输入因素为销售税金及附加的税率.

接着，通过BP神经网络的正向输入计算出项目的投资利润率、项目的投资利税率、以及项目自有资金财务净现值，并且把计算出的这些值作为BP神经网络的中间信息.

最后，在已知期望输出——即给定的行业的投资利润率为20%，投资利税率为25%的基础上，将已经计算出来的输出信息与给定的期望输出作比较，当项目投资利润率大于20%，项目的投资利税率大于25%，并且项目自有资金财务净现值大于零时，将该项目视为可行.

以上计算的前提是BP神经网络的输入信息，即销售税金及附加的税率不变.但是由于经济因素的不确定性，税率的变化往往会受到市场以及国家政策变化的影响.而BP神经网络是一个整体机制，一个输入信息的变化必然会引起全局的变化，因此，销售税金及附加的税率的变化必然会影响到项目的可行性.

为了在投资决策阶段对项目的可行性做到充分的预测，我们应该利用BP神经网络的误差反向传播，在假定项目可行的基础上求出输入信息——这里是销售税金及附加的税率的边际值.这样，就可以在已知项目的销售税金及附加的税率变化的前提下，对项目可行性达到更准确更快捷的预测.

具体计算过程如下：

根据给定条件，编制项目总成本费用估算表，如下表[8]：

表中：年折旧费=[固定资产投资总额×1-残值率）]筑性：

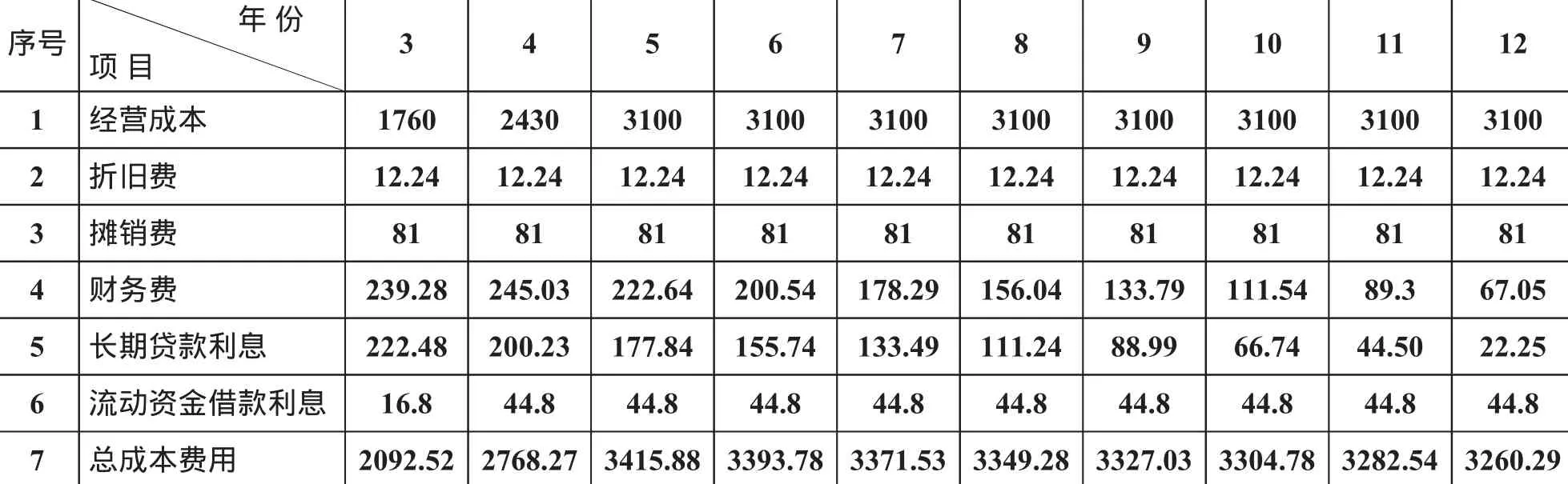
表2 某项目总成本费用估算表单位：万元

表3 某项目损益表单位：万元

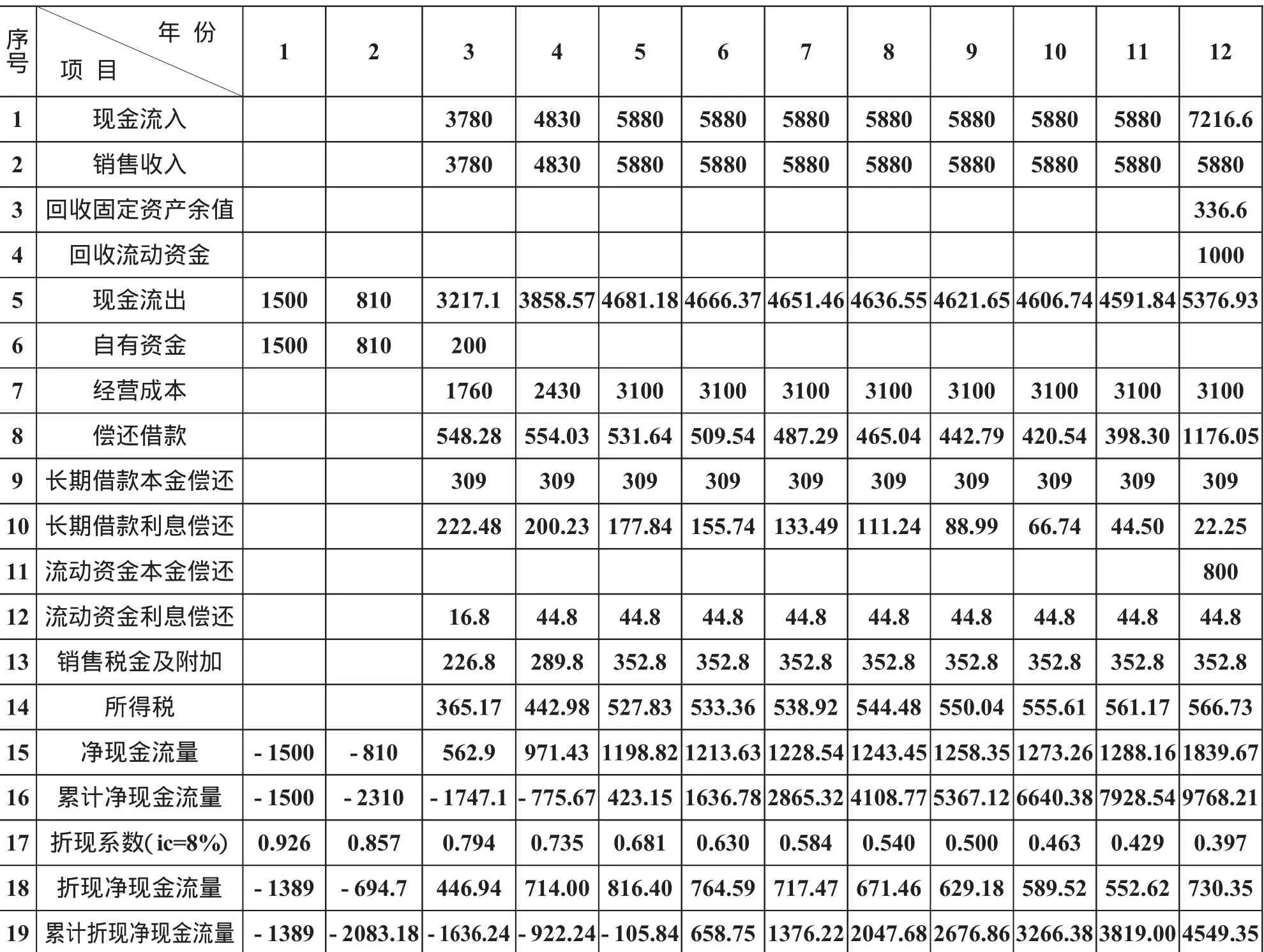
表4 自有资金现金流量表

因为项目投资利润率为32.1%>20%,项目的投资利税率为32.38%>25%，项目自有资金财务净现值NPV=4549.35万元>0,项目在全寿命期的盈利能力大于行业水平.所以，可以判定该项目从自有资金财务评价的盈利能力指标法分析也是可行的.

以上的计算均是按照BP神经网络的计算原则，从正向计算所得到的结果.而下面的计算则是继正向计算之后，按照误差的反向传递来研究项目的可行性.这点也是本文研究的重点之所在.

这里假设项目是可行的，这样，就可以确定期望输出——即给定的行业的投资利润率为20%，投资利税率为25%.而在这两个比率已经确定的基础上按照误差反向传递的原则，反推计算，从而确定出输入信息的临界值.具体计算过程如下所示.

这里的反推过程确定了输入信息即长期贷款利率的临界值.不过，这里的输入信息只是在其他影响因素不变，只有长期贷款利率变化的前提下进行计算的.笔者只是研究单一因素变化对项目可行性的影响.其具体计算过程如下：

假定项目是可行的，因此，项目的投资利润率必须要大于20%，投资利税率必须要大于25%.这里假设销售税金及附加的税率为x，就可以得到：

=（∑年利税÷n÷项目总投资）×100%

这里假设项目可行，即项目的投资利税率>25%,假设销售税金及附加的税率为y,同理可得：

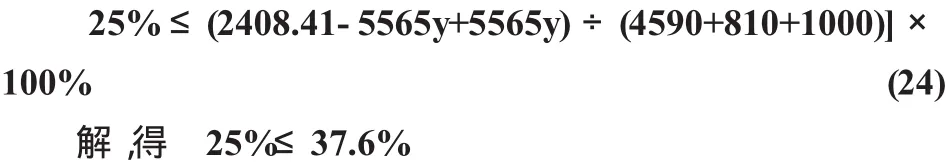
即得到一个恒成立的不等式，也就是说该项目投资利税率的取之与项目的销售税金及附加税率无关.

综上，我们得出销售税金及附加的税率必须小于等于20.3%.

5 模型的检验及得出的结论

5.1 预测模型的检验

通过以上的计算过程可知，当销售税金及附加税率小于等于20.3%时，该项目的投资利润率必然大于等于20%.而又因为项目的投资利税率与销售税金及附加税率无关，而同时通过以上计算可知，项目的净现值大于零.因此，可以得出项目时可行的.从而也说明通过BP神经网络预测模型得出的预测结果时正确的.

5.2 结论

在完成了BP神经网络的正向计算以及其误差的反向传递计算之后，我们就可以达到在项目的投资决策阶段，对项目的可行性更快更好的预测的目的.当只考虑单一因素变化时，销售税金及附加的税率大于20.3%时，项目必然不可行；而只有在这一税率小于等于20.3%时，项目才是可行的.本文这里只是考虑销售税金及附加的税率这一个单一因素的变化给项目的可行性带来的影响.同理，当影响项目的投资决策阶段的其他因素变化时，我们也可以采用BP神经网络的预测原理，对单一影响因素下的项目的可行性达到充分的预测.

〔1〕吴现立.冯占红.工程造价控制与管理[M].武汉:武汉理工大学出版社，2004：l-219.

〔2〕朱嫌.建设工程造价管理[M].北京:中国建筑工业出版社，1998：1-189.

〔3〕程鸿群.工程造价管理[M].武汉：武汉大学出版社，2004.：15-16.

〔4〕周志华.草存根.神经网络及其应用[M].北京：清华大学出版社，2004：384-386.

〔5〕朱大奇.神经网络的研究及应用[M].北京：科学出版社，2005：13-15.

〔6〕杨东侯，年晓红，杨胜跃.两种改进的BP神经网络学习算法.长沙大学学报，2004(4):51-54.

〔7〕冯为民，曹跃进，任宏.基于案例模糊推理的土木工程造价估算方法究.土木工程学报，2003(3):51-56.

〔8〕王维，贺京同，等.人工神经网络在非线性经济预测中的应用.系统工程学报，2000，15(2):65-69.

TU723.3

A

1673-260X（2010）11-0080-04