基于动态规划的房地产投资决策模型构建
2010-09-15简彩云
简彩云
(湖南商务职业技术学院,长沙 410205)
基于动态规划的房地产投资决策模型构建
简彩云
(湖南商务职业技术学院,长沙 410205)
房地产投资具有典型的高收益、高风险特征,企业应通观全局,以极其谨慎的态度进行投资决策分析。文章在分析影响房地产投资收益因素的基础上,借助管理科学中的动态规划模型理论,将价格变动率、单位建筑成本变动率、费用变动率三个动态变量引入房地产投资决策过程,构建了房地产投资决策的非线性模型,并通过实例证明运用此法进行房地产投资决策是完全可行有效的。
投资收益;非线性规划;模型;实证研究
房地产投资是房地产开发商根据政府出让的土地,在规定的容积率内,进行楼盘开发并实现销售的活动。房地产投资回收周期较长,在为企业带来丰厚收益的同时,也需要企业投入巨额的资金并承担巨大的资金风险。因此,房地产企业在取得土地和办理规划许可证前,应当通观全局,以极其谨慎的态度对取得的土地及拟开发项目进行投资决策分析。本文基于对房地产投资决策的实际研究,借助管理科学中的动态规划理论,建立了房地产投资决策分析与评价的非线性模型,从理论与思维上修正了线性决策法的缺陷与不足,为房地产投资决策提供了新的思路与方法,并首次在房地产投资决策中加以运用,证明运用此法进行房地产投资决策是完全可行有效的。
1 房地产项目投资非线性决策
1.1 投资收益线性决策
在不考虑影响房地产项目投资收益诸因素变动的情形下,投资收益可用公式表示为:
投资收益=销售收入-投资额-费用-税金。即:

其中:I—投资收益;S—销售收入;C—投资额;F—费用;T—税金。
某房地产项目在确定的投资开发周期内,在确定成本、费用、税金及市场价格不变或销售单价、单位土地成本、单位建筑成本、费用率等一定时,投资与收益呈现线性关系,企业的投资分析只需根据公式(1)计算某类型楼盘每平方米的投资收益,并进行比较,企业便可做出投资决策。在企业仅开发较为单一的楼盘时,这种方法尤为简单适用。此时,其投资决策分析的一般程序是:在该块地规定的容积率内确定可承建的最大建筑面积;根据市场行情确定各类型楼盘建筑面积;确定价格、成本、税金、费用水平;预测其收益水平。
1.2 投资收益非线性决策
房地产是一种特殊商品,开发周期长,市场供给与需求具有有限弹性。在实际操作中,由于房地产市场价格的波动、建筑成本与费用等的不定性,投资与收益并不呈现简单的线性关系,纯粹的线性关系根本不可能存在:
(1)当某房地产项目超过一定的投资规模后其成本与费用会因规模经济而降低,房产价格也会随着销售量的增加及回款速度加快而呈现下降变动趋势;
(2)随着投资规模的扩大,开发周期延长,建筑材料、人工费上涨又会使成本费用上升;
(3)在GDP呈现正常增长的经济形势下,随着投资规模扩大,开发周期延长,人们收入增加,房地产商品的价格往往会呈递增趋势。
总之,在不同的投资时间、不同的投资额下,项目的价格、成本及费用水平也会有所不同,企业应根据投资额确定开发周期,在开发周期内根据市场及企业实际研究其变动情况,对项目投资做出最优决策。
因此,借助简单而传统的模拟线性关系的方法进行投资决策分析将会给企业带来投资决策的非理性,甚至会导致投资决策错误,这在企业开发的楼盘项目为多类型或房地产市场价格动荡不稳时表现得会更为明显。如何对非线性关系下房地产投资决策问题进行决策,提高房地产企业投资决策水平,是我国房地产企业目前所面临的一个现实难题。
2 基于动态规划的非线性模型建立
2.1 基本原理
动态规划是解决多阶段决策过程的最优化的一种方法,在经济管理、最优控制等方面得到了广泛的应用。动态规划主要用于求解以时间划分阶段的动态过程优化问题,一些与时间无关的静态规划中的最优化问题,只要人为的引进时间因素,将其视为多阶段决策过程,就可以用动态规划方法进行求解。房地产投资可视为一个动态的过程,以商品住宅开发为例,企业可以假定各类型楼盘的投资额为不同的投资阶段,并将各阶段投资划分为不同等份的投资额,求取最优方案。在房地产投资与收益存在非线性关系时,应用动态规划原理进行房地产项目投资与收益决策更加符合市场现实情况。
2.2 非线性模型的建立
2.2.1 影响我国房地产企业投资收益的因素分析
影响我国房地产企业投资收益的因素有很多,其形成既复杂且充满变数,既与企业内部的开发成本费用有关,又与市场供求、消费预期、土地管制、银行政策等市场与政府行为有关。在各影响因素中,无论哪一因素发生变化,都将是牵一发而动全身。因此,对房地产项目的投资分析应当采用系统观点,对投资收益的形成与变动进行动态地分析。这里,我们借用有名的波特“五力模型”来分析其影响因素。
“五力模型”由波特(Porter)提出,是用来分析企业所在行业竞争特征的一种有效工具。波特认为,行业中存在着决定竞争规模和程度的五种力量,这五种力量综合起来影响着产业的吸引力。借用Porter的思想,我们可以构建影响我国房地产企业投资收益的“三力系统”,如图1所示。

在“三力系统”中,房地产企业的投资收益高低主要取决于市场行为(市场竞争、供求及消费预期等)、企业行为(如企业开发成本与费用)及政府行为(土地政策、税率)三方面的力量大小。其中,市场、企业及政府又各自形成其对应的子系统,企业投资收益的稳定性、变动性以及由此而形成的新的投资决策是基于这三个子系统间或内部因素相互作用、相互影响的共同合力,形成房地产项目投资收益。
2.2.2 构建我国房地产企业投资决策非线性模型
(1)非线性模型的建立。基于对影响我国房地产企业投资收益因素的分析,在现有线性决策模型中,可以推定:当所购土地的建筑面积被确定后,单位土地成本随即确定,不会变化;税率是国家决定的,短期内一般不会变化(如果实际发生变化,企业也是难以预计的)。因此,在新的模型建立中,我们只需考虑房地产项目未来的市场价格、单位建筑成本、费用水平对投资收益的影响,无需考虑单位土地成本与税率对投资收益的影响,则公式(1)可换算为:
投资收益=销售面积×销售单价×价格变动率-销售面积×(单位土地成本+单位建筑成本×单位建筑成本变动率)-直接投资额×费用率×费用变动率-收入×税率
其中:直接投资额=销售面积×(单位土地成本+单位建筑成本×单位建筑成本变动率)
收入=销售面积×销售单价×价格变动率
经整理,房地产投资收益非线性决策模型用公式可表示为:
投资收益=销售面积×销售单价×价格变动率 (1-税率)-销售面积×(单位土地成本+单位建筑成本×单位建筑成本变动率)(1+费用率×费用变动率)
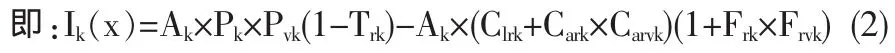
其中:k—各类型楼盘(k=1,2,…,n),x—k 类楼盘的投资份额(x=1,2,…,m),Ik(x)—k 类楼盘投资 x 的收益,Ak—k类楼盘建筑面积;Pk—k类楼盘均价,Pvk—k类楼盘价格变动率;Trk—k类楼盘税率;Clrk—k类楼盘单位土地成本;Cark—k类楼盘单位建筑成本,Carvk—k类楼盘单位建筑成本变动率;Frk—k类楼盘费用率;Frvk—k类楼盘费用变动率。
(3)模型的改进。本模型综合考虑了影响投资收益各因素的变动情况,将税率与单位土地成本作为静态变量,而将价格变动率、单位建筑成本变动率、费用变动率3个变量作为动态变量,有助于房地产企业合理而科学地进行投资决策。
2.3 应用非线性模型进行投资决策过程
2.3.1 获取基础数据
应用非线性模型进行投资决策应获取的基础数据为:根据市场行情,对拟开发的各类型楼盘进行品质定位、价格预测;对已确定的各类型楼盘确认单位建筑成本及成本变化;确定费用率及费用变化;根据投资额确定各类型楼盘可建最大面积与不同投资额下的建筑面积;根据投资额确定单位土地成本;确定税率。
2.3.2 优化投资收益
用k表示待开发的各类型楼盘,将投资额分成若干等份,以 x表示(x=1,2,3,……,m);计算当 k=1,2,…,n 且 x=1,2,…,m时的投资收益并列表;运用动态规划非线性模型进行优化,求得最优方案(详见本文实证分析)。
3 非线性模型求解实证分析
本文以长沙某房地产开发有限公司 (以下简称为A公司)在大河西先导区开发各类型商品住宅为例进行投资决策分析。该公司于2007年6月在大河西先导区取得土地1宗,土地面积为300亩,土地单价为40元/亩,容积率小于1.2(可建最大面积24万平方米)。拟计划投资5.5亿元,开发低密度的双拼别墅、联排别墅、洋房及普通住宅。其投资决策过程如下:
3.1 获取基础数据
以长沙市同地段同类型B、C公司楼盘为参考楼盘,测算出以下基础数据:
3.1.1 销售单价
根据对B、C等楼盘的分析,A公司初步确定各类型楼盘均价分别为:双拼5800元,联排4800元,洋房3800元,普通住宅3000元(单位:元/平方米)。同时,根据双拼、联排、洋房、普通住宅投资与价格的变动及规模经济的影响,确定以5500万元为投资起点,每增加5500万元在原价格的基础上增加相应的折扣率 (双拼为0.015、联排为0.01、洋房为0.005、普通住宅为0)。以洋房为例,即投资5500万元时,销售单价为3800元/平方米;投资11000万元时,销售单价为3800×(1-0.005)元/平方米。
3.1.2 建安成本(工程费用)
以B、C公司楼盘为参照,A公司测算各类楼盘单位建安成本如表1。
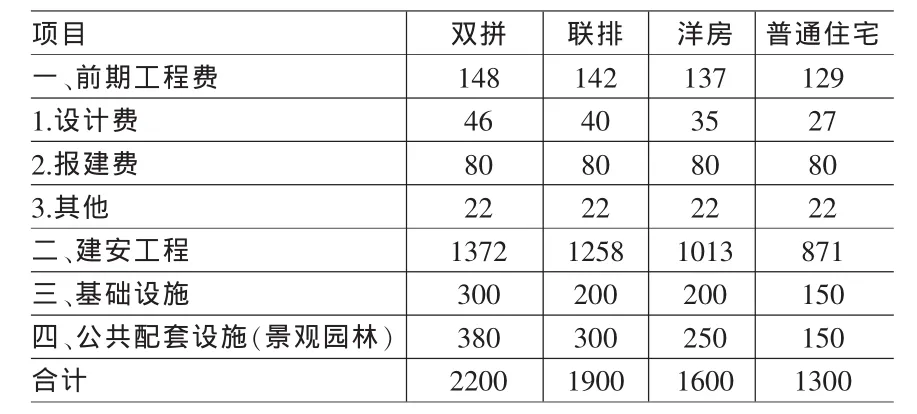
表1 A公司各类楼盘单位建安成本预测表 单位:元/平方米
3.1.3 开发费用
根据房地产开发企业一般费用水平和土地增值税扣除依据,按土地开发成本与建筑成本的10%扣除,确定开发费用率为10%(注:因投资规模较小,无需考虑费用水平的变化)。
3.1.4 建筑面积
(1)各类住宅可建最大面积
本项目土地总成本为12000万元(300亩×40万元/亩)。由公式“投资总额=土地总成本+建安总成本+开发费用”可计算得出双拚、联排、洋房、普通各楼盘可建最大面积分别为15.2066万平方米、17.6076万平方米、20.9091万平方米、25.7343万平方米。以双拼为例,开发费用按土地总成本与建安总成本之和的10%计算,即:55000=(12000+2200×可建最大面积)×1.1,求出双拚可建最大面积为15.2066万平方米。
(2)各类型不同投资额下的建筑面积
将投资额5.5亿元划分成10等份,以5500万元为起点,逐次累加,转化成不同金额的投资额,并以此计算出不同投资额下的建筑面积 (建筑面积=投资额×可建最大面积/最大投资额)。

表2 A公司各类楼盘不同投资额下的建筑面积 单位:万元、万平方米
以投资2.2亿元联排别墅为例,其建筑面积为:2.2×17.6076/5.5=7.04(万平方米)
依此类推,计算出各类住宅不同投资额下的建筑面积(见表 2)。
3.1.5 土地成本
根据土地总成本与各类楼盘可建最大面积,可求出双拼、联排、洋房、普通住宅楼盘的单位土地成本(单位土地成本=土地总成本/可建最大面积)分别为789.13/元平方米、681.52 元/平方米、573.91 元/平方米、466.30 元/平方米。
3.1.6 税金
(1)营业税及附加税费。根据现行税收政策,营业税按销售收入售价5%,城市维护建筑税按营业税7%计算,教育费用附加按营业税4.5%计算,营业税及附加税费合计按销售收5.575%确认。
(2)土地增值税。根据长沙市现行土地增值税核定征收比例确认,双拼和联排按销售收入的3%确认,洋房和普通住宅按销售收入的1%确认。
(3)企业所得税。根据长沙市现行房地产开发企业核定征收比例确认,即按收入的3.75%确认。
由以上可推出,双拼和联排别墅单位税金按销售单价的12.325%确认,洋房和普通住宅单位税金按销售单价的10.325%确认。
3.1.7 投资收益
(1)将投资总额5.5亿元划为10等份,以x表示,x=1,2,3,……,10;
(2)当 k=1,2,3,4 且 x=1,2,…,10 时,计算投资收益(见表 3)。

表3 A公司各种投资额可获得的投资收益 单位:万元
以投资联排别墅2.2亿元为例,投资收益计算过程如下:
将 k=2;x=4;A2=7,04;P2=4800;Pv2=(1-0.03)=0.97;Clr2=681.52;Car2=1900;Carv2=1;Fr2=0.1;Frv2=1;Tr2=0.12325 代入公式(2)得:I2(4)=8751(万元)
3.2 投资收益优化
A公司将5.5亿元的投资问题可分为4个阶段 (开发一个楼盘类型即为一个投资阶段),在第k阶段就是要确定项目k的投资额,投资额以X表示,X=1时,投资额为5500万元。 依此类推,X=10时,投资额为 5.5亿元(X=1,2,……,10)。
令:uk为对项目1直到项目k-1投资后的剩余资金金额;xk为对项目 k 的投资额;ωk(uk,xk)为对项目 k 投资金额 x k 后的收益 ωk(xk);fk(uk)应对剩余资金 uk对项目 k,k+1,k+2,…,n,投资可获得的最大收益。显然,状态转移方程为:uk+1=uk-xk
为了获得最大利润,必须将5.5亿元全部用于投资,故假设有第5阶段存在,必有于是有下列递推方程:
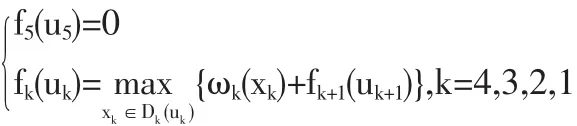
(1)当 k=4 时,有:D4(uk)={u4}
f4(1)=1563,f4(2)=3125,f4(3)=5769,f4(4)=7693,f4(5)=9616,f4(6)=11539,f4(7)=13462,f4(8)=15385,f4(9)=17308,f4(10)=19232
(2)当 k=3 时,有:
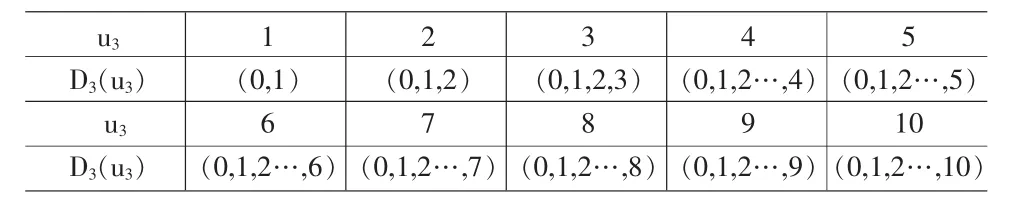
u3 1 2 3 4 5 D3(u3)u3 D3(u3)(0,1)6(0,1,2…,6)(0,1,2)7(0,1,2…,7)(0,1,2,3)8(0,1,2…,8)(0,1,2…,4)9(0,1,2…,9)(0,1,2…,5)10(0,1,2…,10)
f3(1)=max{ω3(1)+f4(0);ω3(0)+f4(1)}=max{2125+0;0+1563}=2125
f3(2)=max{ω3(2)+f4(0);ω3(1)+f4(1);ω3(0)+f4(2)}=max{4,179+0;0+2125+1563;0+3125}=4179
同理,f3(3)=6162;f3(4)=8073;f3(5)=9948;f3(6)=11931;f3(7)=13854;f3(8)=15777;f3(9)=17700;f3(10)=19624
(3)当 k=2 时,u2、D2(u2)与 u3、D3(u3)的取值范围分别相同。 计算结果为:f2(1)=2410;f2(2)=4672;f2(3)=6797;f2(4)=8911;f2(5)=10876;f2(6)=12947;f2(7)=14912;f2(8)=16824;f2(9)=18716;f2(10)=20682
(4)当 k=1 时,有:u1=10,D1(u1)={1,2,…,10}

应用逆序追踪法知,最优投资方案为:
x1*=4,x2*=3,x3*=3,x4*=0 时,即双拼投资 2.2 亿元(建筑面积为6.08万平方米)、联排投资1.65亿元 (建筑面积为5.28万平方米)、洋房投资1.65亿元(建筑面积为6.27万平方米)、多层住宅为0时,最大投资收益为22486万元。且双拼、联排、洋房建筑面积总计为17.63万平方米,小于24万平方米(容积率1.2),符合政府部门的规划要求。
3.3 投资决策收益
A公司于2007年下半年对该项目进行开发,并按照以上双拼、联排、洋房面积承建,至2009年已基本销售完毕,已获净利23258万元。如不考虑价格、成本、费用同时变动而用线性决策法进行决策,A公司将会仅选择开发双拚别墅 (单位投资额为5500万元时,收益2733万元为最大收益)。如果公司选择了仅开发双拚别墅,在价格、成本、费用发生变化时,实际收益仅为16889万元(见表3),公司将会损失6369万元。
4 结束语
房地产项目的成功,投资决策至关重要。成熟的市场和激烈的竞争客观上要求开发商在了解市场需求的基础上,准确定位,科学决策。本文所用非线性决策方法适用于房地产企业各类投资决策,不管是商品住宅还是商业用房等,尤其是在房地产价格、成本、费用同时变动时更能体现这一方法的决策优势。
[1]曹喜望.管理科学中的数学模型[M].北京:北京大学出版社,2006,(1).
[2]秦广庆,叶祥松.基于动态规划的生产计划优化模型研究[J].改革与战略,2009,(1).
[3]何雄飞,马林东.基于实物期权方法的房地产投资决策灵敏度分析[J].现代商业,2009,(24).
(责任编辑/亦 民)
F224.9
A
1002-6487(2010)17-0051-04
简彩云(1964-),女,湖南桃源人,硕士,副教授,研究方向:房地产经营管理。
