上海金属期货与现货市场非对称波动溢出效应的实证研究

陈 锋，高展军

（西北政法大学 经济管理学院，西安 710063）

上海金属期货与现货市场非对称波动溢出效应的实证研究

陈 锋，高展军

（西北政法大学 经济管理学院，西安 710063）

运用二维非对称BEKK-GARCH模型，考察了上海金融期货与现货市场间收益率的非对称波动溢出效应。实证结果表明：样本期铝期货与现货收益率间存在双向的波动溢出效应，而铜期货与现货收益率波动溢出效应不显著；铜、铝期货、现货市场间都存在双向的波动非对称效应，都对来自对方市场的“消息”的冲击有显著的反应。

波动溢出效应、波动非对称性、向量GARCH模型

1 研究方法

金融研究与实务领域，无疑更关注两市场之间收益率条件均值的变动和相互作用，这也是本文研究的主要目的，因此需要建立多元GARCH模型来考察市场间波动溢出效应。

Kraft，Engle(1983)提出了向量ARCH类模型，设一个维向量随机序列：

在式（1）中，Mt为其均值向量，{εt}是一个 N×1 维向量随机序列，且有εt|It-1～N(0,Ht),It-1是到t-1时刻的信息集，Ht是N×N维正定矩阵，且关于It-1是可测的。定义ht=Vech(Ht)，Vech（·）称为向量半算子，表示把矩阵Ht的下三角阵按列依次堆积而成的N(N+1)/2维向量，向量GARCH类模型主要是研究Ht的不同动态特性。

此后，Bollerslev，Engle 和 Wooldridge（1988）提出扩展的向量GARCH模型中Vech(Ht)形式表示为：

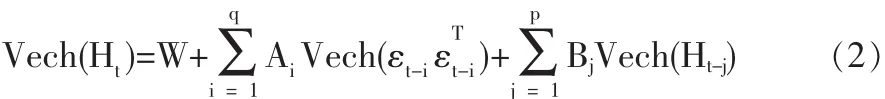
其中，W为N(N+1)/2维向量，Ai和 Bj均为[N(N+1)/2维方阵，且 Ai和 Bj使 Ht正定，i=1,2,3…p,j=1,2,3…q。

向量GARCH模型非常适合分析多市场之间的波动溢出效应，模型参数矩阵Ai和Bj中的对角线元素反映方差、协方差序列自身的相关关系；而非对角线元素反映了不同变量的方差、协方差序列之间的相互影响，但向量GARCH模型的缺点参数过多，估计比较困难，而且实际运用中很难保证Ht正定。

Engle 和 Kroner(1995)在综合 Baba，Engle，Kraft和 Kroner的研究基础上提出了一种实施正定限制的参数化模型，简称为BEKK-GARCH模型，其模型表示如下：

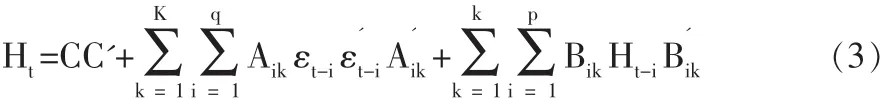
式（3）中，Aik和 Bik为 N 维方阵，C 是[N(N+1)/2]的上三角阵，当K=P=q=1，简化的BEKK-GARCH(1,1)模型可以表示为式（4）：

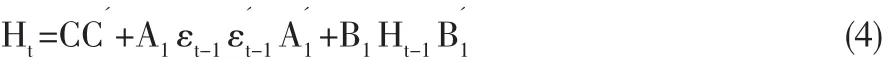
BEKK-GARCH模型的优点是容易满足Ht的正定，待估计的参数也相对较少，但模型中参数的经济学涵义相比于向量GARCH模型不够明确。在式(4)BEKK模型中往往假设残差项εt服从多元正态分布，而现实中金融时间序列往往呈现“尖峰厚尾”的特征，并不能完全服从正态分布，t分布或广义误差分布（GED）相比正态分布能更好的反映序列的“尖峰厚尾”的特征。

Kroner和Ng(1998)在BEKK-GARCH模型的基础上，提出包含一般动态协方差的非对称BEKK模型（Asymmetric BEKK）。 令 ηit=max[0,-εit]和 ηt=[η1t…ηNt]，则非对称 BEKK 模型可以被定义为式（5）的形式：

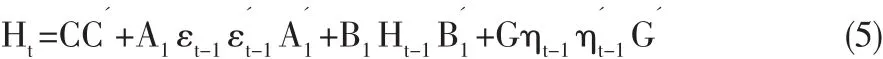
其中，G为N维方阵，且ηit为负值，代表了坏消息对Ht产生的冲击影响，只需G方阵中所有元素显著不为0，就说明存在着非对称的杠杆效应。

国外文献中BEKK-GARCH模型的运用主要有：Karolyi(1995)使用BEKK-GARCH模型估计了美国和加拿大股票市场收益率间的波动关系；Kearney and Patton(2000)运用BEKK-GARCH模型分别估计了三个、四个和五个汇率市场间的波动溢出效应；Worthington和Higgs(2004)运用BEKKGARCH模型检验了亚洲市场间的波动溢出关系；都取得了良好的估计效果，国内文献中主要在对中国股票市场研究中介绍或使用过该模型，期、现货市场间波动性研究尚没有文献涉及。

本文目的是考察上海金属期货与现货市场间的波动性关系，建立二维的非对称BEKK-GARCH模型，参数方阵Aik、Bik和Git中，令i=1,2，其中1代表现货市场，2代表期货市场。二维非对称BEKK-GARCH模型的展开式可以表示为下面（6）式的形式，其中对角线参数反映各市场自身的相关关系；非对角线参数（a12,a21）、（b12,b21）反映期货与现货两市场间的波动溢出效应；（g12,g21）反映期货与现货两市场间的波动非对称性。本文考察重点是上海金属期、现货两个市场间的溢出效应，我们将针对模型参数方阵中非对角线元素的非线性组合进行似然比LR统计量和Wald统计量的检验。对上海铝、铜期、现货市场之间的波动溢出效应作如下检验：

（1）原假设 H0:a12=b12=0,a21=b21=0，不存在期货与现货市场间双向的波动溢出效应；

（2）原假设H0:a12=b12=0，不存在现货市场对期货市场的单向波动溢出效应；

（3）原假设H0:a21=b21=0，不存在期货市场对现货市场的单向波动溢出效应；

（4）原假设H0:g12=g21=0，不存在期货与现货市场间双向的波动非对称效应；

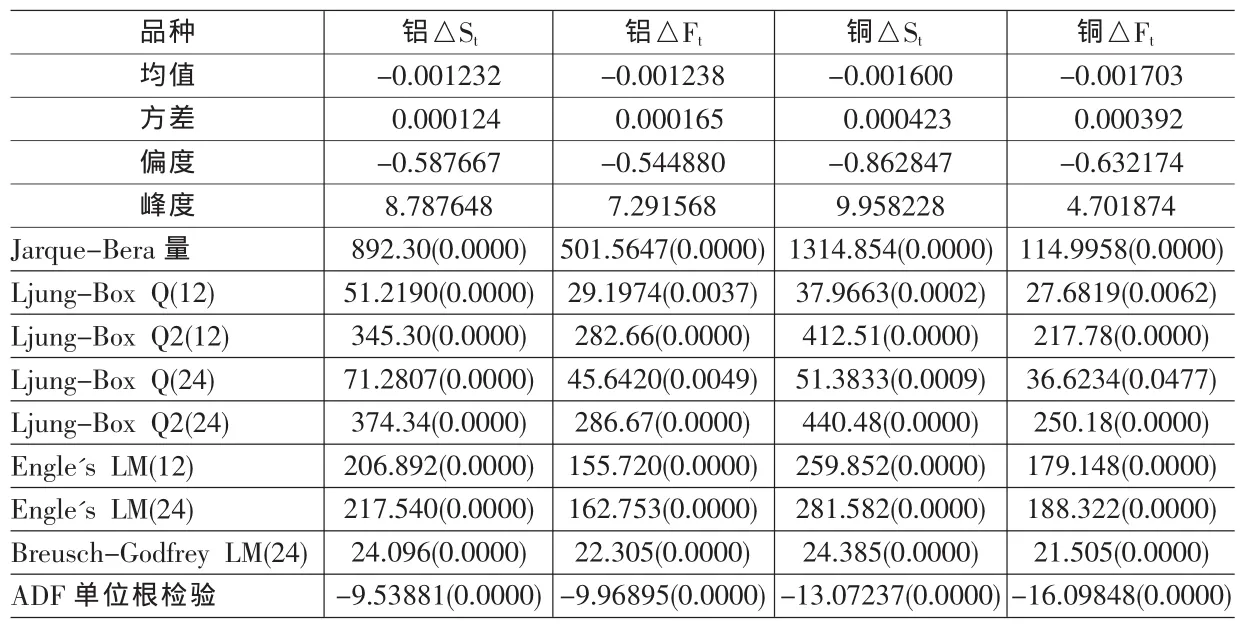
表1 描述统计、ARCH效应检验结果

2 数据说明与ARCH效应检验

2.1 数据说明

本文研究数据选取上海期货交易所铝连续、铜连续合约日收盘价，以及对应期间上海有色金属市场铝、铜现货的日价格。铝期货与现货数据样本期为2006年5月18日至2008年12月9日，共计近30个月615个交易日；铜期货与现货数据样本期为2006年5月30日至2008年12月9日，共计近30个月615个交易日；数据来源于长江有色金属市场网站历史数据资料和彭博期货行情软件。交易日的现货价格与期货收盘价，那么现货日收益率与期货日收益率则分别St为Ft与的一阶差分，表示为△St与现货市场的价格序列定义为St=Ln(Pt)，期货市场的价格序列定义为其中分别是第 t个△Ft，即△St=Ln(Pt/Pt-1)，

2.2 描述性统计和ARCH效应检验

分别对铝、铜现货、期货市场日收益率序列进行描述性统计分析，和收益率序列自相关的Ljung-BoxQ统计量检验、Engle拉格朗日乘数（LM）检验、Breusch-Godfrey LM高阶序列相关检验方法，来检验收益率残差的方差是否存在条件异方差，并且对序列进行平稳性的ADF检验，结果见表1：

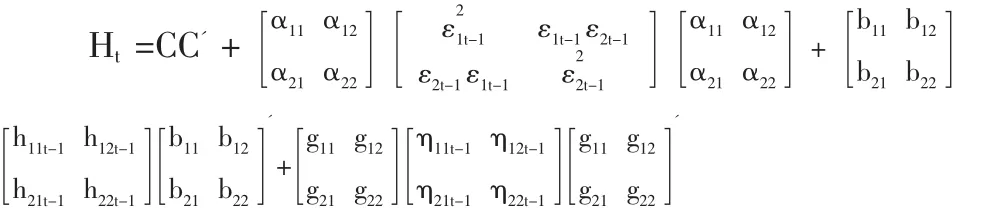
从表1结果可知，在样本期，铝期货市场的方差大于现货市场，表明铝期货市场价格波动程度大于现货市场，而铜市场正好相反，铜现货市场价格波动程度大于期货市场；铝、铜现货、期货市场从偏度来看，均为左偏的，铜市场的偏度较大；从峰度来看,铝、铜现货、期货市场的峰度均大于3，Jarque-Bera统计量均奇大，说明铝、铜现货、期货市场均呈现“尖峰厚尾”的分布，并不能完全符合正态分布。Ljung-Box Q、Engle LM、Breusch-Godfrey LM检验统计量的概率值均显著为0，说明铝、铜现货、期货市场收益率的残差序列均存在条件异方差，即收益率的波动具有随时间推移而改变的自回归条件异方差（ARCH）现象，而且ADF单位根检验铝、铜市场日收益率序列均为平稳序列，适宜于建立ARCH族模型进行分析。

3 实证结果

上海铝、铜现货、期ARCH效应，建立非对称向量BEKK-GARCH(1,1)模型进行实证分析，检验现货收益率与期货收益率间的波动溢出效应是否存在，以及波动溢出是否呈现非对称性。本文采用无约束最货市场收益率均具优化BFGS（Broyden，Fletcher，Goldfarb 和 Shanno）算法来估计使模型似然值极大的参数向量，分别正态分布、t分布和广义误差分布（GED）的假设下，并依据AIC值最小准则选择最优模型。表2为式(6)的估计结果，包括收 益率波动的持续性、自身波动的非对称性、波动溢出效应、波动的非对称性等信息，表3为两市场之间波动溢出及波动的非对称效应检验结果。由表2和表3可得：

（1）从铝、铜现货、期货市场收益率序列自身波动看，即式（6）中Aik、Bik的对角线元素，仅铝期货前一期误差项不显著，其余各参数均在1%置信水平下显著，说明各序列自身波动有明显的持续性；现货、期货市场间，在式（6）Aik中的非对角线元素，只有铝现货与期货市场间具有波动的持续性。

（2）从收益率序列自身波动的非对称性看，即式（6）中的gik对角线元素，除铝现货外，其余均显著性，说明铝现货不存在“热波”效应，即铝现货市场对前一期的“消息”的冲击没有明显反应；铝期货、铜现货和铜期货估计系数均显著不为0，说明从自身收益率序列看，存在波动非对称的杠杆效应，即对各自市场前一期的“消息”冲击有明显反应；

（3）从现货与期货收益率间的波动溢出效应来看，即式（6）中Bik的非对角线元素，铝现货与期货估计系数在1% 显著水平下均显著，说明铝现货与期货市场间具有显著双向跨市场波动溢出效应，既具有“流星雨”效应；而铜市场估计系数均不显著，说明铜现货与期货收益率变动波动性没有显著的跨市场波动溢出效应。

（4）从现货与期货市场间波动非对称性方面看，即式（6）中gik的非对角线元素，在铝市场估计系数均显著不为0，铝现货、期货市场间均具有波动的非对称性，说明在铝现货、期货市场都对来自对方市场的“消息”有明显反应；在铜市场估计系数也均显著不为0，说明铜现货、期货市场间虽没有显著的波动溢出效应，但市场间却存在着显著的波动非对称效应，这一点与Koutmos和Tucker(1996)等人的研究结论相似。

4 结论和未来研究的建议

本文样本期处于“大熊市”时期，期间又爆发了美国“次贷”危机引发的金融“大海啸”，对国际金属市场产生重大影响，在此背景下并结合国外学者及华仁海、刘庆富、张金清等国内学者的相关文献分析如下：

（1）本文结论上海铜市场间的波动溢出效应不显著，与张金清(2006)、刘庆富(2007)的研究结论不相符，本文样本期间位于两人研究期间之后，说明上海铜期货与现货存在显著的双向波动溢出效应,而铜市场间则不显著,我们认为这并不能作为比较两市场成熟程度的依据,两市场这样的差异,可能与两种金属在中国的储藏量、生产量的差异有关，这种差异的存在，造成两市场所受到的影响信息来源上存在不同。结合华仁海（2005），张金清（2006）、刘庆富（2008）的研究结论，可能与铜期货市场的国际化市场间，收益率的波动溢出效应并不是始终存在，不具有一贯性，可能会随市场情况的变化而发生变化，正如Gwilym and Buckle(2001)所指出市场景气循环也是收益率波动效应的重要决定因素；也可能如Min和Najand.(1999)D对韩国KOSPI(200)指数期、现货市场的研究发现市场间波动溢出效应存在显著的样本依赖。

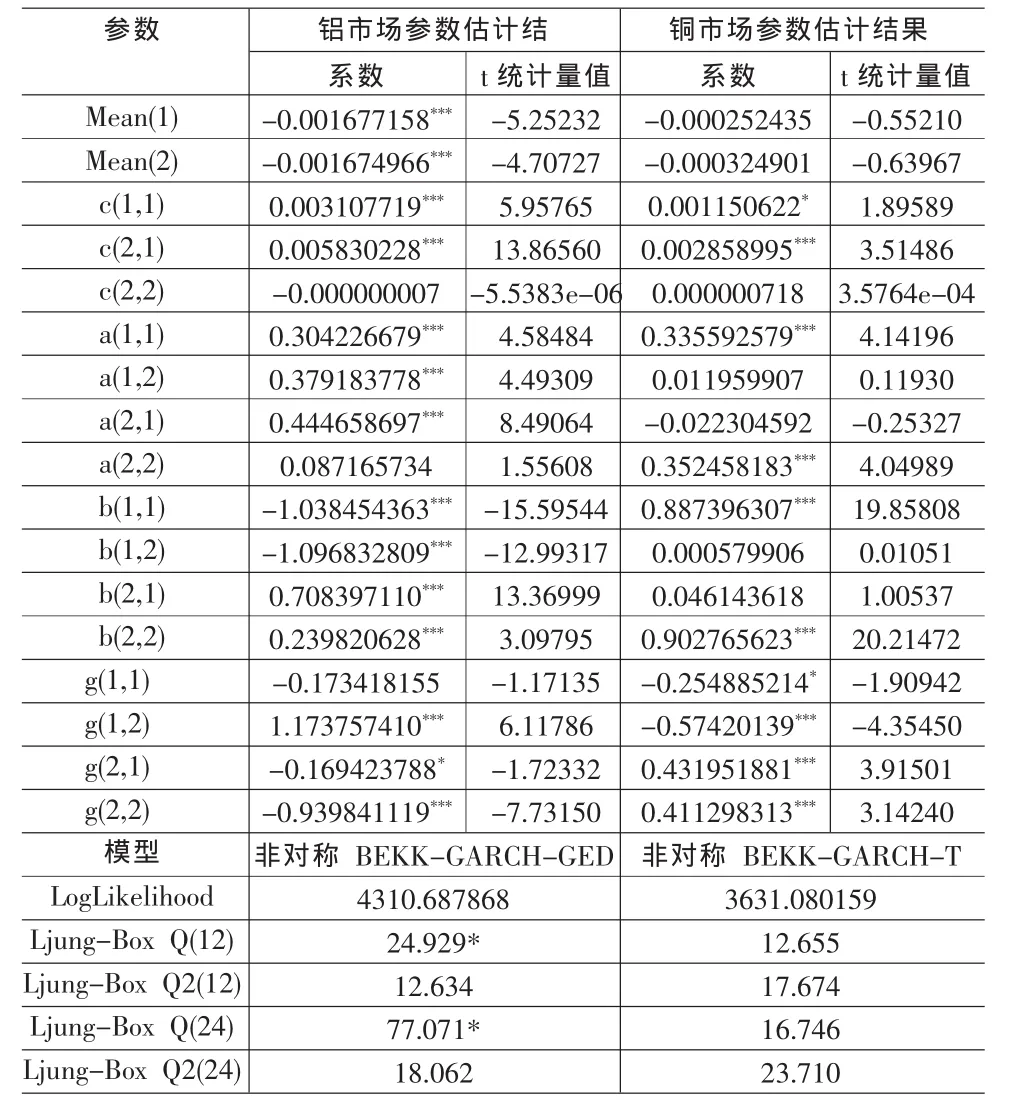
表2 非对称波动溢出效应估计结果

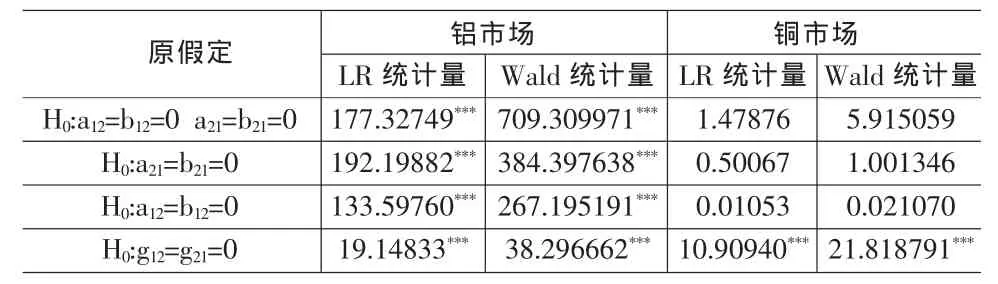
表3 期、现货两市场之间波动溢出及波动的非对称效应检验

（2）在样本期的“大空头”市场，上海铝、铜期货、现货市场间波动溢出效应表现不同，铝期货与现货市场间程度相对较高有关。

（3）上海金属期货与现货市场间存在显著的波动非对称性的杠杆效应，这一点与张金清(2006)、刘庆富(2007)的结论相符，在“大熊市”和国际金融危机的双重打击下，期、现货两市投资者都对来自对方市场的信息有着敏感的反应，但实证结果并不能解释铜市场间的波动非对称效应的产生机理，可能与上海铜期货、现货市场分别受到国际铜期货、现货市场的较强影响有关。

（4）本文以及国内相关文献实证研究中，还存在着没有考虑收益率序列均值样本期在不同域之间变化的问题，忽略域变特点可能会造成波动性测量值相对于真实值出现偏差，从而影响实证结论的精确程度。因此有关中国期、现货市场间波动性的研究还有待进一步的深入。

[1]Black,F.Studies of Stock Markets Volatility Changes,Proceedings of the American Statistical Association[C].Business and Economic Statistics Section,1976.

[2]Stephen A.Ross.Information and Volatility:The No-Arbitrage-Martingale Approach to Timing and Resolution Irrelevancy[J].The Journal of Finance，1989,44(1).

[3]Robert F.Engle,Takatoshi Ito,Wen-Ling Lin.Meteor Showers or Heat Waves?Heteroskedastic Intra-Daily Volatility in the Foreign Exchange Market[J].Econometrica,1990,58(3).

[4]Chui-Chun Tsai,Tsun-Siou Lee.An Investigate on Information Transmission ofNearby-Month Taiwan Stock Index Futures during Trading,Nontrading,and between Trading and Nontrading Period:Price Discovery and Content of Price Volatility[J].Journal of Financial Studies,2004,12(1).

[5]Koutmos,G.,Tucker M.Temporal Relationships and Dynamics Interactions between Spot and Futures Stock Markets[J].Journal of Futures Markets,1996,16(1).

[6][台湾]蔡垂君,李存修.台湾股价指数与指数期货跨市场价量讯息传递关系之实证研究-价格发现与价量关系[J].中华管理评论(国际学报),2004,7(2).

[7]Angelos.Kanas.Volatility Spilloversbetween Stock Returnsand Exchange Rate Changes:International Evidence[J]..Journal of Business Finance&Accounting,Blackwell Publishing,2000,27.

[8]华仁海,刘庆富.国内外期货市场之间的波动溢出效应研究[J].世界经济,2005,(8).

[9]张金清,刘庆富.中国金属期货市场与现货市场之间的波动性关系研究[J].金融研究，2006,(7).

[10]刘庆富,仲伟俊.我国金属期货与现货市场之间的价格发现与波动溢出效应研究[J].东南大学学报(哲学社会科学版),2007,(5).

[11]R F Engle,KF Kroner.Multivariate Simultaneous Generalized ARCH[J].Econometric Theory,1995,11.

[12]张世英,樊智.协整理论与波动模型——金融时间序列分析及应用[M].北京:清华大学出版社,2004.

(责任编辑/易永生）

F724.5

A

1002－6487（2010）17－0150-03