上证指数收益率的ARCH族模型的实证分析

陈志娟

（湖南农业大学 商学院，长沙 410128）

上证指数收益率的ARCH族模型的实证分析

陈志娟

（湖南农业大学 商学院，长沙 410128）

文章利用ARCH族模型，选取2005～2009年的上证综指日收益率作为对象对我国沪市波动情况进行了实证研究。研究结果表明，我国沪市日收益率序列具有明显的聚集性、波动性、尖峰厚尾的特征，ARCH族模型较好的拟合了上证指数收益率序列。

ARCH模型；收益率；波动性

中国股票市场是一个新兴市场，与成熟资本市场相比，制度对市场波动的影响比较明显。波动性代表了未来价格取值的不确定性，股票价格(或指数)的时间序列往往呈现出非平稳性，其方差可能随时间增长而趋于无限。使用ARCH模型的主要好处在于：对条件异方差进行正确估计后可以使回归参数的估计量更具有效性；可以更好地预测随时间变化的被解释变量的置信区间。 本文利用ARCH族模型，选取2005～2009年的上证综指日收益率作为对象对我国沪市波动情况进行了实证研究。

1 模型概述

1.1 EGARCH（指数 GARCH）模型

EGARCH模型又称为指数GARCH（exponential GARCH）。现有文献中有多种表达条件方差方程的方法，本文给出下面两种设定形式是：

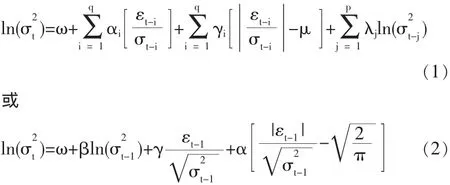
式（1）右侧第2项是用条件标准差σt除以新息（innovation）εt及其滞后项，（εt/σt）表示标准新息，第 3 项是用均值 u减标准新息的绝对值，正新息表示“利好”，负新息表示“利空”。在正新息和负新息绝对值相同的情况下，通过该模型可以区别正、负新息对波动的不同影响，从而检验波动的非对称性或杠杆效应。比起纯粹的GARCH设定来讲，这个模型有几个优点。由于式（2）建立了模型，那么即使参数是负的，也将是正的。因此不需要人为的对模型参数施加非负约束；如果波动性和收益之间关系是负相关的，γ将是负的，所以在EGARCH模型下能解释非对称性。

1.2 GARCH（“门限”GARCH）模型

TGARCH（“门限”GARCH）模型，又称 GJR 模型，与 EGARCH模型一样可以区别“利好”与“利空”消息对波动的不同影响。一般的TGARCH模型形式如下：

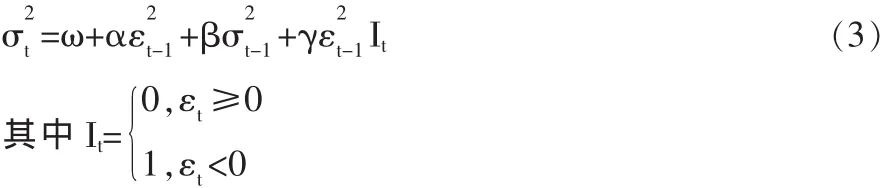
其中 εt＞0 表示“利好”消息，εt＜0 表示“利空”消息。 对于TARCH模型，“利好”和“利空”消息对条件方差的影响是不一样的。当出现“利好”消息时，波动的平方项的系数是α。当出现“利空”消息时，波动的平方项的系数是α+γ。当γ=0时，条件方差对冲击的反应是对称的。当γ≠0时，条件方差对冲击的反应是非对称的，当γ＞0时，称这种现象为杠杆效应。

1.3 CGARCH(Component GARCH)模型

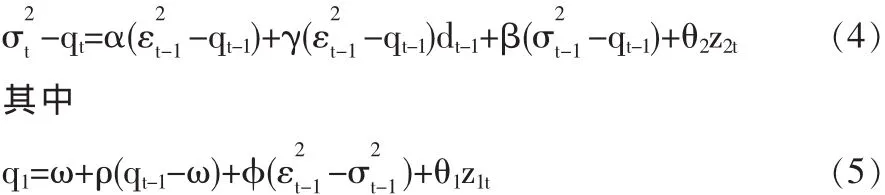
其中，σt仍然是波动性，而qt代替了m，称为时变的长期波动性。式（4）描述的是短期的成分以幂指数 α+β 的势（power,反映衰减速度）收敛于0，式（5）描述的是长期成分qt以幂指数ρ收敛于ω。ρ一般介于0.99和1之间，因此qt以极慢的速度收敛于ω。将短期方程与长期方程结合起来可得到以下方程:

式（6）显示出CGARCH模型实际上是一个非线性的受限制的GARCH(2,2)模型。

在成分ARCH模型的条件方差中,可以包含外生变量。这个外生变量可以放在长期方程中，也可以放在暂时方程中（或者两者均可）。暂时方程中的外生变量将对变化率的短期移动产生影响，而长期方程中的变量将影响变动率的长期水平。

在暂时方程中还可以引入非对称影响，称为非对称的成分ARCH模型，它的条件方差方程的形式为：

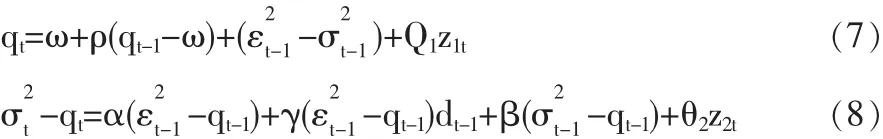
其中：z是外生变量，d是虚拟变量，表示负冲击，当εt-1＜0时，dt=1；否则dt=0。只要γ≠0，冲击就会对变动率的短期波动产生非对称的影响；如果γ＞0，就意味着条件方差中存在暂时杠杆效应。这种非对称效应只出现在短期波动中，对长期波动率的影响则主要体现在系数ρ的变化上。

2 上证指数收益率的波动残差序列分析

2.1 样本数据选取及研究方法

本文以2005年1月1日至2009年12月31日共1823个交易日的上证综指的收盘价格作为样本,样本数据来源于大智慧数据库系统。之所以采用该段时间，是因为在2003年9月以前由于“非典”疫情造成了股市的异常波动，选取此后的数据能减少异常阶段的干扰，提高模型的拟合精度。在计算上证综指日收益率时，采用股指的对数一阶差分形式，设第 t日的收益率为 rt，则 rt=lnpt-lnpt-1，pt是第 t日上证综指的收盘价格。实证分析主要是借助时间序列分析软件E-views 5.0完成的。

2.2 基本统计特征分析

由收益率序列yt的图形可知：上证指数的对数收益率在0上下频繁波动，并且在一次大的波动后往往伴随着大的波动，一次小的波动后往往伴随着小的波动，反映出股市存在暴涨暴跌现象。统计显示出序列不服从正态分布，呈现出的“尖峰厚尾”的分布特征。

2.3 收益率序列的平稳性检验和相关性分析

首先对序列{Rt}进行ADF单位根检验，其结果见表1。

其ADF值为-30.9459，小于1%的Mackinnonl临界值-3.4389，因此拒绝序列非平稳的零假设，即序列{Rt}平稳。

表1 上证指数收益率变量单位根检验结果

对样本期内收益率序列{Rt}的偏自相关系数偏自相关函数(PACF)进行判断,并利用L jung-BoxQ统计量诊断,发现日收益率序列PACF函数在滞后期29以后有截尾特征，即是一个29阶自回归过程。对{Rt}建立AR(29)模型,回归结果显示只有AR(6),AR(14),AR(15),AR(29)的系数是显著的。估计收益率序列关于自身之后项的自回归模型为:

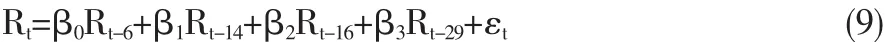
回归结果如下：

对回归方程(9)做ARCH效应的LM检验,其结果见表2：

表2 上证指数收益率变量ARCH效应检验结果

LM统计量Obs*R-squared P值为0.007，小于显著性水平α=0.05，拒绝原假设，即{Rt}存在ARCH效应；当检验阶数取2到10时的相伴概率P均接近于0,说明序列存在高阶ARCH效应,上证指数收益序列AR模型的残差平方序列存在高阶自相关。由于一个高阶的ARCH模型可以用一个低阶的GARCH模型代替，因此用GARCH(1，1)模型描述收益率序列的自相关性使恰当的。其均值方程和条件方差方程分别如下：

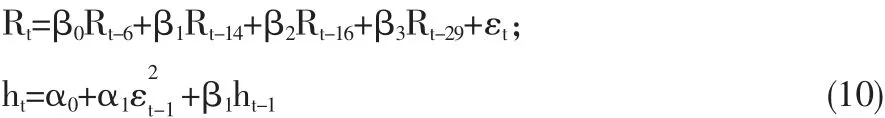
结果如表3：

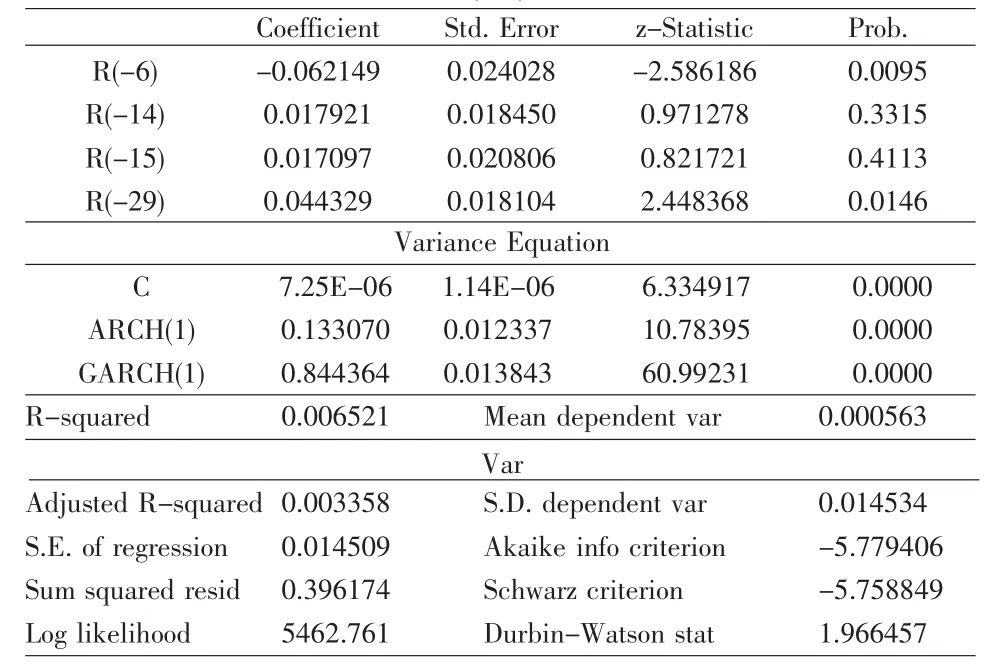
表3 GARCH(1,1)模型数据表

在GARCH（1，1）模型的估计结果可知，沪市存在明显的杠杆效应。利空消息更会引起股票市场更大的波动，从而证实选择GARCH(1,1)模型来拟合收益率序列的易变性是合适的，EGARCH模型的估计结果与GARCH模型估计的结果一致。

2.4 拟合与预测

为了得到模型的预测能力，首先用所建立的AR(29)-GARCH(1,1)模型，对所做数据进行拟合，通过下面两个图形（图2、图3）的对比可以看出拟合结果较好，说明GARCH(1,1)模型能较好的应用到股票市场数据分析中。

3 结论与建议

(1)沪指波动率统计上呈现显著的“聚集”现象,说明存在着ARCH 效应，暂时方程中非对称系数的显著性,表明了杠杆效应的存在性。这种杠杆效应说明了负的冲击比正的冲击带来的波动更大，具有与美国等发达国家资本市场股价、股市同性质规律也得到一定程度的验证。

(2)从EGARCH模型可知，外部冲击对CPI年增长率的波动性是非对称的，即“利空冲击”能比等量的“利好冲击”产生更大的波动。由于“利空冲击”能比等量的“利好冲击”产生更大的波动，当出现“利空冲击”时，政府有必要对不成熟的市场经济进行有效的调控，以保持物价的稳定。

（3）从各模型参数的显著性水平来看，EGARCH模型在t分布和GED分布下参数的显著性水平都很高，特别是t分布下的EGARCH模型很好地描述了沪市收益率序列显著的波动聚类、尖峰厚尾、非对称性和杠杆效应等特征。

[1]黄海南,钟伟.GARCH类模型波动率预测评价[J].中国管理科学,2007,15(6).

[2]Tseng C H,et al.New Hybrid Methodolgy for Stock Volatility Prediction[J].Expert Systems with Applications,2008,(36).

[3]Wang Y H.Nonlinear Neural Network Forecasting Model for Stock Index Option Price:Hybrid GJR-GARCH Approach[J].Expert Systems with Applications,2007，（10）.

[4]Tseng C H,et al.Artificial Neural Network Model of the Hybrid EGARCH Volatility of the Taiwan Stock Index Option Prices[J].Physica,2008,A(387).

[5]汪来喜,丁日佳.基于GARCH 模型的股票期权定价方法研究[J].金融理论与实践,2008，(2).

[6]牛方磊,卢小广.基于ARCH类模型的基金市场波动性研究[J].统计与决策,2005，(12).

[7]H Drees,L de Haan,S Resnick.How to Make a Hill Plot[J].Annals of Statistics,2000,28.

[8]唐平，刘燕.基于宏观经济变量的中国股市波动分析[J].财经科学，2008，（6）.

[9]魏宇，余怒涛.中国股票市场的波动率预测模型及其SPA检验[J].金融研究,2007，(7).

[10]Ruey S.Tsay[美].金融时间序列分析[J].北京:机械工业出版社,2006.

（责任编辑/易永生）

F832

A

1002－6487（2010）17-0141-03

陈志娟（1975-），女，湖南桃江人，硕士，讲师，研究方向：会计系、经济学。