允许缺货时存储空间存在限制的存储模型
2010-09-14鲁亚男
鲁亚男, 刘 欣, 姜 鹏
(沈阳化工大学数理系,辽宁沈阳 110142)
允许缺货时存储空间存在限制的存储模型
鲁亚男, 刘 欣, 姜 鹏
(沈阳化工大学数理系,辽宁沈阳 110142)
针对经济订购批量公式假设中存储空间无限大这一条件不符合实际问题提出改进方案,即按原有存储空间容量订货,允许缺货,承受缺货损失,并在此方案上建立存储模型,通过求此模型的最优解,讨论在总平均费用最小意义下的最优存储决策,并通过实例验证模型的可行性.
经济订购批量公式; 受限存储空间; 总平均费用; 缺货; 存储决策
存储问题是经济管理中的一个基本问题. 1934年威尔逊 (W ilson R.H.)从经济的角度研究如何确定最佳存储数量问题,给出了存储论中著名的经济订购批量 (Economic ordering quantity)公式,简称 E.O.Q.公式[1].为了进一步增加E.O.Q.公式的适用范围,国内外很多学者对其进行各种改进[2-6].虽然可研究的方向很多,但对存储空间存在限制且允许缺货的存储模型研究却很少,K.J.Chung等人在可延迟交货情况下,针对不易腐烂物品建立了存储空间容量受限制的二级库存优化模型[6];周涛等人在对多品种配送库存优化模型的研究中对此也有涉及[7],2篇文章都将存储空间容量存在限制作为约束条件来建立存储模型,并求解给出了最优决策,但文章只是将这一限制作为一种硬性条件来看待,没有提出当存储量超过存储空间容量时的解决途径.李温红仅对仓库容量有限条件下的不允许缺货的存储模型进行了研究[8],而刘德权,陈有禄等人虽然针对仓库容量有限条件下的允许缺货存储模型进行了研究[9-10],但其给出的模型是采用租赁仓库方式下的模型,忽略考虑当租赁仓库费用很高时的情况.本文就这一情况,提出针对仓库容量有限条件下的另一种解决方案,即按照原有仓库容量订货,承受缺货损失,并给出其数学模型,求出最优解.
1 允许缺货时存储空间存在限制的存储模型
1.1 模型假设
模型假设如下:
(1)需求是连续的、均匀的;
(2)一次订货量无最大、最小限制;
(3)采购、运输均无价格折扣;
(4)当存储降至 0时,可以立即得到补充;
(5)每次订购费不变,且与订货量无关;
(6)每次订货量不变;
(7)单位存储费不变,维持存储的费用是存储量的线性函数;
(8)存储空间有限.
1.2 基本模型
允许缺货时,按现有存储空间容量订货并承受缺货损失的一个订货周期内总费用为:


1.3 模型分析


图 1 原有存储空间的存储量变化Fig.1 Change of the storage quantity in the original space
上诉总费用模型(1)式共分 3个部分,其中第 1部分为 1个订货周期内存储空间的存储费用:

第 2部分为一个订货周期内的缺货费用:

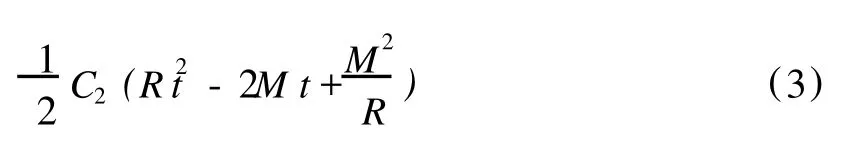
第 3部分为订购费C3.
1.4 模型求解
将(1)式除以t,得一个订货周期内的总平均费用为:

由于当C2>0时,C(t)在(0,+∞)上是t的严格凹函数,所以t0也是C(t)在(0,+∞)上的唯一最小值点,而C(t)的最小值为:


证明: 按现有存储空间容量订货,产生缺货费用,须Q>M或R t-M>0.
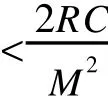
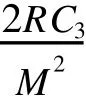
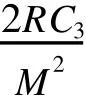
2 实例验证
例: 某企业某种物品的需求率为 100件/ d,订购费用每次为 3 500元,自己公司的仓库能容纳该物品 300件,使用自己仓库的单位存储费用为 1元.单位物品单位时间的缺货损失为 1.5元.请帮助该企业确定一个好的存储方案.
解: 分析题意,得各参数值如下:

将以上数据代入 E.O.Q.公式,可得存储空间不受限制时:
最优订货周期为t0=8.37 d;
最优订货量为Q0=837件;
最优总平均费用为C0=837元.
注意到由 E.O.Q.公式计算得到的最优订货量超过了原有存储空间的容量,原有存储空间将无法容纳下 837件物品,这表明此时 E.O.Q.公式将不再适用,需要寻求其他的方案来解决此问题.

将例中的各数据代入 (5)式,得出按现有存储空间容量订货情况下的最优订货周期为t0= 7.37 d.由于t0的值不是整数,所以分别计算在t=7及t=8时的总平均费用.
将t=7代入(4)式,得总平均费用为C= 736元,再将t=8代入(4)式,得总平均费用为C=728元.
经比较可知,该公司应采用按现有存储空间容量订货并承受缺货损失的存储方案,这时总平均费用最低,为 728元.最优订货周期为 8 d,订货量为 300件.
3 结束语
传统的经济订购批量公式 (E.O.Q.公式)是在存储空间无限及不允许缺货的假设前提下研究的,然而这一假设条件与实际并不相符,针对这一情况,给出允许缺货时存储空间存在限制的新的存储模型及其最优解.并通过实例验证了其可行性.
[1] 钱颂迪.运筹学 [M].北京:清华大学出版社, 1990:356-358.
[2] Sarker B R,Jam al A M,W ang S J.Supply Chain M odels for Perishable Products under Inflation and Pem issible D elay in Paym ent[J].Computers and Operations Research,2000,27(1):59-75.
[3] 王瑛,孙林岩.基于合作需求预测的多级库存优化模型[J].系统工程理论方法应用,2004,13(3): 208-213.
[4] 陈顺正,宋国防,杨国东.基于混合需求多产品的供应链库存优化模型[J].上海大学学报 (自然科学版),2005,11(3):314-319.
[5] D iponegoro A,Sarker R.D eterm iningM anufacturing Batch Sizes for a Lumpy D elivery System with Trend D em and[J].International Journal of Production Econom ics,2002,77(2):131-143.
[6] Chung K J,Huang T S.The Optim al Retailer’s O rdering Policies forD eteriorating Item s with L im ited Storage Capacity under Trade Credit Financing[J]. International Journalof Production Econom ics, 2007,106(1):127-145.
[7] 周涛,程钧谟,乔忠.多品种配送的库存优化模型研究[J].系统工程,2003,21(5):19-23.
[8] 李温红.仓库容量有限条件下的不允许缺货存储模型[J].系统工程理论方法应用,1997,6(3):68 -71,80.
[9] 刘德全,徐毓,孙知建.仓库容量有限条件下的允许缺货存储模型[J].空军雷达学院学报,2002,16 (1):22-23.
[10]陈有禄,罗秋兰.仓库容量有限条件下的允许缺货存储模型[J].广西工学院学报,2001,12(4):85 -87.
The Storage Decision on Lim ited Storage Space Perm itting Stockouts
LU Ya-nan, L IU Xin, JIANG Peng
(Shenyang U niversity of Chem ical Technology,Shenyang110142,China)
In view of Econom ic O rderQ uantity form ula unlim ited storage space does not accord with reality.This paper offers the storage m odelwith lim ited storage space perm itting stockout,and discusses the optim um storage decision under m inim um average total cost and gives the feasibility study through instance.
econom ic order quantity; lim ited storage space; average total cost; stockout; storage decision
O227
A
1004-4639(2010)04-0376-04
2010-01-19
鲁亚男(1978-),女,辽宁沈阳人,讲师,硕士,主要从事最优化方法的研究.
