Joukowsky翼型绕流流场的计算网格划分
2010-09-14李成植
李成植
(沈阳化工大学机械工程学院,辽宁沈阳 110142)
Joukowsky翼型绕流流场的计算网格划分
李成植
(沈阳化工大学机械工程学院,辽宁沈阳 110142)
针对 Joukowsky翼型复杂的型线特点,推导微分法生成其绕流流场计算网格的公式,并采用 FORTRAN语言编写计算机程序.结果表明:所生成的计算网格不但具有贴体的特征,同时还具有其环形网格线由里及表渐疏布局的特点,而这一特点正是符合黏性流体绕流流场的计算要求;另外,微分法所生成的网格系的辐射状和环形网格线之间以及辐射状网格线与翼型型线之间的正交性较好,有利于进一步提高数值计算精度.
Joukowsky翼型; 贴体网格; 微分法; Poisson方程
Joukowsky翼型是基于Joukowsky变换,由计算平面上圆心位于第二象限的偏心圆变换而来的翼型.计算其绕流问题,通常有 2种途径,一种是通过保角变换法,另一种则是数值计算方法.保角变换法是基于计算平面的圆柱绕流和物理平面上的翼型绕流之间保角变换的特点,由已知计算平面上的圆柱绕流流场推算物理平面上的翼型绕流流场的方法.采用保角变换法的前提是在计算平面上能够引入复位势,但由于复位势的实部是速度势函数,所以,保角变换法只能适用于那些求解理想流体的绕流问题.在求解实际流体的 Joukowsky翼型绕流问题时,可采用数值方法进行求解.就目前而言常用的数值方法有有限元法、有限体积法和有限差分法.其中,有限元法因为对边界的要求不是很高,所以越来越受到计算流体力学界的关注,而有限差分法和有限体积法较之有限元法而言其方法的物理意义比较明确,是人们进行流场数值仿真的传统方法,其方法和理论也比较成熟.但无论是有限差分法,还是有限体积法,均对计算区域边界形状的要求高.例如 Joukowsky翼型等曲线边界的情况,如采用传统的方法进行网格划分,则会有边界网格节点不能落在物面上的情况出现.此时,只好采用线性或多项式插值(外推)的方法建立起边界节点流动参数和物面流动参数之间的关系,并由物面的流动参数推算边界节点上的流动参数.但其结果不但降低了计算的准确度,而且还增加了程序的复杂性.为避免传统网格划分方法所带来的不便,在不规则计算区域的网格划分中,可采用微分法生成贴体坐标的方法来生成计算网格.微分法生成网格,依据的是由 Laplace方程所定解的坐标变换,在其定义域内满足最大值和最小值必定在该区域边界上的特点[1].但是,Laplace方程定解的坐标变换不能满足控制网格疏密度要求,而 Poisson方程定解的坐标变换,既有 Laplace方程定解坐标变换的特点,同时又能满足控制网格疏密度的要求.
本文基于 Joukowsky变换设计 3款Joukowsky翼型,并用微分法生成Joukowsky翼型绕流流场的计算网格,为 Joukowsky翼型绕流的数值计算打下基础.
1 Joukowsky翼型
Joukowsky变换可将计算平面上的圆心在 (c-acosβ,asinβ)点,半径a=c(1+λ)secβ为的偏心圆变换到物理平面上的 Joukowsky翼型,其变换关系近似为[2]:

由 Joukowsky变换得到的 Joukowsky翼型最大的相对厚度和相对弯度分别为[2]:

基于(1)式由表 1所示数据为控制参数的 3款 Joukowsky翼型型线如图 1所示.由图 1可以看出:2#翼型不但具有一定的厚度而且还有一定的弯度,因此该款翼型既有一定的强度又能满足产生一定升力的要求.相对于 2#翼型,1#翼型和3#翼型则分别显得过于单薄和弯度不够.

表 1 Joukowsky翼型控制参数和特性数据表Table 1 The control parameter and special property of Joukowsky’s airfoil

图 1 Joukowsky翼型型线图Fig.1 The thread of Joukowsky’s airfoil
2 微分法生成计算网格
根据黏性流体流动的特点,在 Joukowsky翼型绕流的数值计算中,必须要虑及边界层的存在,而边界层内流向的速度在边界层厚度方向的方向导数大,因而在边界层内黏性力与惯性力相当.在边界层外的势流区,流向速度在横向的方向导数可视为是零,因而可以忽略黏性力的存在.为准确地刻画黏性流体绕流 Joukowsky翼型的上述特点,所划分的网格要求具有由翼型表面至无限远处是由密渐疏的特点.而 Poisson方程定解的坐标变换能够满足控制网格疏密度要求,所以以 Poisson方程定解的微分方程来完成由规则的计算区域中的矩形网格到 Joukowsky翼型绕流区域的正交曲线网格系的变换,其变换方程和定解条件为[3]:


图 2 变换原理图Fig.2 The principle of change
利用差分法离散控制方程,则得计算物理平面上对应网格节点坐标的显式迭代方程:

说明:以上差分方程左侧为下一时刻的值,而右侧则是采用该时刻的值;变换平面上纵、横网格步长为 1.
采用 FORTRAN语言编写(1)式和(3)式的计算机程序,在划分网格的程序部分采用将物理平面上的计算网格从翼型后缘点处剪开,等ξ网格线是逆时针方向递增排列的方案.
3 结果与分析
用 COORD INA TE CONV ERSION程序计算生成了如图 1所示的 3款 Joukow sky翼型绕流流场的贴体网格,并采用 Tecplot软件进行后处理,其结果如图 3和图 4所示.
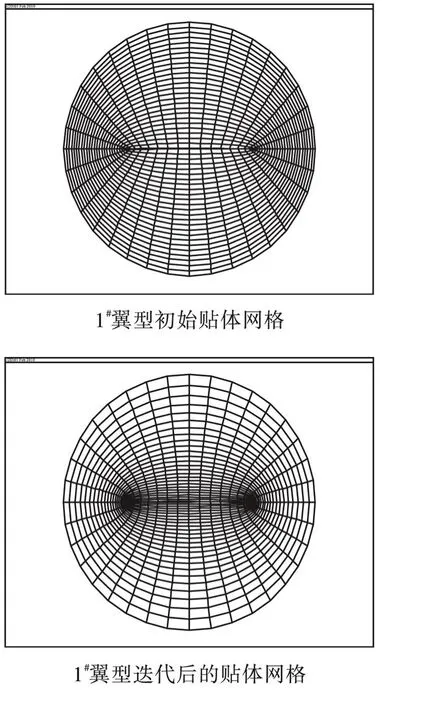

图 3 Joukow sky翼型绕流网格划分图Fig.3 The m esh of Joukawsky’s airfoil


图 4 3#翼型迭代前、后前缘点附近网格对比图Fig.4 Contrast figure betw een before iterative and after iterative for near the front-r im dot
由图 3可以看出:初始的网格系统虽然是贴体的,但环形网格线,即η网格线却是等间距布局的.基于这种等间距布局的网格系统进行数值计算时,为充分地刻画边界层内急剧变化的流向速度,只好在整个计算区域内加密环形网格线,即加大η网格线的密度.但这种全区域加密η网格线的举措,对于进一步提高占据计算区域绝大部分的势流区的计算精度不会有太多的帮助.显而易见,为了加密边界层内的网格密度付出了增加计算工作量的代价.而通过 Poisson方程定解的坐标变换法所生成的贴体坐标系,则通过适当地选取控制η网格线的参数Q,实现了η网格线在计算区域内由里及表渐疏的布局,在不增加计算工作量的前提下,满足了加密翼型附近网格的要求.图 4为迭代前、后 3#翼型前缘点附近的网格放大图,从图 4可以看出:经过迭代之后其网格线的正交性得到了极大地改善,其中辐射状网格线,即ξ网格线与翼型型线之间正交性的改善尤为明显.对于有限差分法和有限体积法,网格线之间正交性的这种改善,有利于进一步提高数值计算的精度.
4 结 论
基于 Joukow sky变换,生成 3款 Joukow sky翼型,并根据 Poisson方程定解的坐标变换在其定义域内最大值和最小值必定会在该区域边界上以及能够通过非齐次项控制网格疏密度的特点,生成了由 Poisson方程定解的微分网格系统.结果表明:所生成的微分网格系统,其最内部η网格线与翼型型线相重合的同时,η网格线分布是由里及表渐疏的非等间距分布,η网格线的这种布局迎合了黏性流体绕流流场的边界层和势流区内速度变化的特点,在不增加计算工作量的前提下,能够提高计算的准确度.另外,Poisson方程所定解的微分网格系统的ξ和η网格线之间以及ξ网格线与翼型型线之间的正交性好,有益于进一步提高数值计算的精度.
[1] 章本照,印建安,张宏基.流体力学数值方法[M].北京:机械工业出版社,2003:248-251.
[2] 吴望一.流体力学 (下册)[M].北京:北京大学出版社,1983:86-90.
[3] 周正贵.计算流体力学——基础理论与实际应用[M].南京:东南大学出版社,2008:106-123.
The Mesh Generation of the Coil-flow Fields for the Joukowsky's Airfoil
L I Cheng-zhi
(Shenyang U university of Chem ical Technology,Shenyang110142,China)
Based on the complex shape-lines of the Joukowsky's airfoil,the coil-flow flow fields were got by using differential method and computer programs were w ritten in the FORTRAN language.The results showed that the computational mesh not only had a body-fitted feature,but also had a layout feature thatwas from the inside to outside.And the feature was in confor m ity with the requirements of the calculation of viscous fluid in the coil-flow flow field;Lastly,the mesh generated by differentiation method had a better orthogonally be tween the radial and the coil lines,as well as be tween the radial and the airfoil lines;this mesh is better for the accuracy of numerical calculation.
joukoaw sky's airfoil; body-fitted m esh; differentiation m ethod; poisson equation
TP39
A
1004-4639(2010)04-0356-04
2010-02-26
李成植(1964-),男,黑龙江尚志人,副教授,博士,主要从事流体力学及其相关学科的教学与科研.
