关于 Hilbert符号的进一步讨论

2010-09-14吴茂全裴晓雯鲁亚男

沈阳化工大学学报 2010年4期

关键词：辽宁沈阳素数整数

吴茂全, 裴晓雯, 鲁亚男

(沈阳化工大学数理系,辽宁沈阳 110142)

关于 Hilbert符号的进一步讨论

吴茂全, 裴晓雯, 鲁亚男

(沈阳化工大学数理系,辽宁沈阳 110142)

Hilbert符号; 二次乘幂; 簇; 稠密

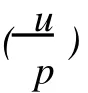
1 必要结论

有理数Q是域,可以做为子域插入Qp和R中,如果a,b∈Q＊(乘群),记(a,b)P(或(a, b)∞)表示Qp(或R)中的 Hilbert符号.定义V是由素数和∞构成的集合.而习惯记Q∞=R,则Q对于所有v∈V在Qv中稠密.为了问题的研究,下面的定理和引理是必要的.由参考文献 [1],以下结论成立.

定理 1(Hilbert定理):如果a,b∈Q＊,则(a,b)v=1几乎处处成立,且

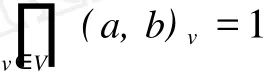
这里的“几乎处处”是指除了有限个数外都成立.

引理 1(剩余定理):设a1,a2,…,an,m1,m2,…,mn是整数,且ai,mi(i=1,2,…,n)是互素对,则存在一个整数a,使a≡ai(modmi)(i=1,2,…,n).

引理 3(狄利克雷定理):如果a,m是互素的整数,且a,m≥1,则存在无穷多个素数p满足p≡a(modm).

2 关于 Hilbert符号的有理数存在定理

有了上面的定理和引理做为基础,在参考文献[2]给出的 Hilbert符号的计算公式基础上,对Hilbert符号在Q＊的一个有限簇与数簇之间的关系进行研究和探讨,总结出下面的关于 Hilbert符号的一个结论.

定理 2:设(ai)i∈I是Q＊的一个有限簇, (εi,v)i∈I,v∈V是等于 ±1的数簇,则对所有的i∈I,v∈V存在元x∈Q＊,使(ai,x)v=εi,v成立的充分必要条件是满足下面 3个条件:

证明

必要性:由定理 1,条件 (1)、(2)成立.取xv=x,则条件 (3)成立.

充分性:设(εi,v)是等于 ±1的数簇且满足条件(1)、(2)、(3).由(ai)i∈I的结构,在用某个整数的二次乘幂乘以ai后,可以假设所有ai都是整数.设S是由∞、2以及ai的素因子所构成的V的子集,T是满足存在i∈I,使εi,v=-1的v∈V构成,则T与S是有限集.下面分两种情形证明:

因为S∩T=Φ,则整数a和m是互素的,由引理 3,存在一个素数p∉S∪T,满足p≡a(modm).下面将证明x=ap具有要证明的性质,即对所有i∈I,v∈V,(ai,x)v=εi,v.

如果v∈S,因为S∩T=Φ,所以εi,v=1.下面检验(ai,x)v=1成立.若v=∞,由x>0可知(ai,x)v=1显然成立;如果v是一个素数l,有x≡a2(modm),因此,当l=2时,x≡a2(mod8),当l≠2时,x≡a2(modl);又因为x,a是l进单位,由参考文献[1]的定理可知x是中的一个二次乘幂,所以(ai,x)v=1.

如果l∉T∪{p},则x是l进单位,因此vl(x)=0,此时上述公式变成(ai,x)l=1;另一方面,因为l∉T,所以 εi,l=1.如果l∈T,有vl(x)=1,由条件(3),存在xl∈对所有i∈I,满足(ai,xl)l=εi,l;由于l∈T,所以εi,l中之一等于 -1,因此vl(xl)≡1(mod 2),则

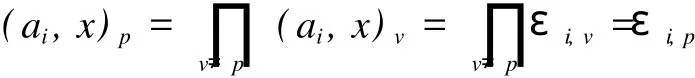
(2)一般情形

[1]知,的二次乘幂构成的一个开子群,再由上述引理 2(逼近定理),存在x′∈Q＊,使对所有v∈S都有x′/xv是中的一个二次乘幂.特别地,对所有v∈S,(ai,x′)v=(ai,xv)v=εi,v.如果令ηi,v=εi,v(ai,x′)v,则簇(ηi,v)适合条件(1)、(2)、(3),而且如果v∈S,则ηi,v=1.由情形(1)所得结论知存在y∈Q＊,使对所有i∈I和v∈V,有(ai,y)v=ηi,v,设x=yx′,显然x就是所求.

综合上述情况 (1)、(2),定理 2成立.

至此推得了对给定的 Hilbert符号(a,b),对于一个有限簇(ai)i∈I和元素等于 ±1的数簇(εi,v),i∈I,v∈V之间存在有理数x∈Q＊,使(ai,x)v=εi,v成立的充分必要条件.它可看作Hilbert符号的又一个性质,对 Hilbert符号的进一步研究有重要的参考价值.

参考文献:

[1] Serre Jean-Pierre.A Course in A rithm etic[M].N ew York:Springer-Verlag N ew York Inc,1993:3-23.

[2] 吴茂全,裴晓雯.关于 Hilbert符号的讨论[J].沈阳化工大学学报,2007,21(3):235-237.

On the FurtherDiscussion of Hilbert Symbol

WU M ao-quan, PEI Xiao-wen, LU Ya-nan

(Shenyang U niversity of Chem ical Technology,Shenyang110142,China)