基于模糊聚类和Zernike矩的自适应水印算法

余楚迎，李建忠，张伯泉

（1.汕头大学物理系，广东 汕头 515063；2.韩山师范学院数学与信息技术系，广东 潮州 521041；3.广东工业大学计算机学院, 广东 广州 510006）

基于模糊聚类和Zernike矩的自适应水印算法

余楚迎1，李建忠2*，张伯泉3

（1.汕头大学物理系，广东 汕头 515063；2.韩山师范学院数学与信息技术系，广东 潮州 521041；3.广东工业大学计算机学院, 广东 广州 510006）

基于模糊聚类和Zernike矩技术，提出一种抗几何攻击鲁棒的自适应图像水印算法.首先根据人眼视觉系统的掩蔽特性，并利用模糊C-均值聚类算法自适应地选择适合嵌入数字水印的位置，然后通过奇异值分解将水印信息嵌入到宿主图像.实验结果表明，该算法不仅具有较好的透明性，而且能有效地抵抗旋转、缩放、翻转和旋转-缩放组合等几何攻击，同时对JPEG压缩、滤波和图像增强等常见攻击也有较好的鲁棒性.

自适应水印算法；模糊C-均值聚类；Zernike矩；几何攻击

0 引 言

随着网络和多媒体技术的迅猛发展，数字水印技术作为数字版权保护的一种有效手段得到了广泛的关注和应用. 但如何有效抵抗如旋转/缩放/平移（Rotation/Scaling/Translation，RST）等几何攻击仍然是数字水印领域所面临的最大困难，也是研究的热点之一.近年来，聚类技术被引入到数字领域[1-6]，这类算法结合人类视觉系统（HVS）的掩蔽特性和聚类分析技术，自适应地确定出水印的嵌入位置或强度，可有效地提高水印算法的透明性.此种算法采用模糊聚类技术自适应地确定数字水印嵌入位置，然后在空域嵌入水印，具有较好的透明性，但抗JPEG压缩攻击性能较弱[1].应用模糊C-均值聚类算法（FCM）选择适合嵌入水印的位置后，将水印嵌入到宿主图像的小波域中，从而提高了算法的鲁棒性[2-3].然而，上述算法均不能有效地抵抗几何攻击.利用聚类技术将宿主图像的小波树系数分为2类，分别嵌入值为1和0的水印信息，可抵抗缩放及小角度旋转攻击[6]，但不能有效抵抗大于0.75°的旋转（含带旋转的组合攻击）以及平移、翻转等几何操作.而利用伪Zernike矩的幅度具有旋转不变的性质，并结合奇偶量化技术所提出的一种自适应RST不变水印算法，并没有真正在宿主图像中嵌入水印信息[7]，本质上是零水印算法.本研究结合上述思想，提出了一种基于模糊聚类分析和Zernike矩的水印算法.该算法结合人眼视觉掩蔽特性和图像的局部相关特性，自适应地选择适合嵌入的区域，并利用量化方法将水印信息嵌入到所选择分块的最大奇异值中.水印检测过程中，先用基于Zernike矩的图像校正算法对几何失真图像进行校准，然后用校正后的图像检测水印.该算法在提取水印信息时不需要原始载体图像，并且由于图像几何校正方法使得水印信息重同步，因此能较有效地抵抗几何攻击.

1 基于Zernike矩的几何校准算法

1.1 Zernike矩定义

单位圆内图像 f（x，y）的 Zernike 矩定义[8]如下：

1.2 翻转校准

设Apq和分别为图像f（x，y）水平翻转前后的Zernike矩，由Zernike矩定义有：当q为偶数时，当q为奇数时，类似地，设为垂直翻转后的 f（x，y）的Zernike矩，则无论q是奇数还是偶数，都有因此，通过Zernike矩的变化可有效地判断图像是否被翻转.在检测到翻转类型后，对失真图像进行校正，如果为水平翻转，则将其水平翻转；否则，对其进行垂直翻转操作，所得到的翻转图像即为校正图像.

1.3 缩放校准

设 f（x/β，y/β）为缩放变换后的图像， Apq和分别为图像变换前后的Zernike矩，则缩放因子β可由下式得到：

根据式（2）计算出β后，对失真图像进行1/β的缩放操作，所得图像即为校正图像.

1.4 旋转及旋转-缩放校准

设f（x，y）被旋转α， 则旋转后的图像的Zernike矩A′pq与原图像的Zernike矩Apq的关系如下：

式（3）表明Zernike矩对于旋转攻击来说只有一个相位的平移.因此，可根据Zernike矩的相位信息来估计图像的旋转角度α：

由式（4）得到α后，先将失真图像旋转－α得f′，然后根据下文1.3节的方法计算f′的缩放因子β，以1/β为缩放因子，对f′进行缩放变换得f″，则f″为校正图像.这里，如果β=1，则失真图像仅被旋转攻击；否则，图像被旋转-缩放组合攻击.

2 模糊均值聚类算法

FCM是一种应用广泛的聚类算法，通过反复迭代优化目标函数来实现数据分类.设数据集 X={x1，x2，…，xn}为给定的 n个样本， FCM 的目标函数定义[1，3]如下：

式（5）中， U={uij}为隶属度矩阵； V={v1，v2，…，vm}为m 个聚类中心点的集合； uij为第j个样本xj隶属于第i个聚类中心vi的隶属度；m为分类个数，且2≤m＜n；γ∈[1,∞）为加权指数；是xj到vi的距离.具体算法[6，9]如下：

1）给定聚类类别数m，并确定加权指数γ，设置迭代计数变量z=0，并随机初始化聚类中心；

3）若‖U（z）－U（z-1）‖≤ε，则停止，否则返回2）继续迭代.

3 奇异值分解

奇异值分解由于具有旋转不变、转置不变和镜像变换不变等重要特性[9]，广泛应用于图像处理、图像压缩和数字水印等领域.图像矩阵是一个实数矩阵A∈RN×N，对其进行奇异值分解：

式（6）中，N×N为图像矩阵大小，r是A的秩，U和V都是正交矩阵，S为对角矩阵，其对角元素λi称为矩阵的奇异值，且满足λ1≥λ2≥…≥λr≥λr+1=…=λN=0.

4 基于Zernike矩的自适应水印算法

4.1 水印嵌入位置的选择

研究表明[10]，图像中亮度高、纹理复杂的区域内可嵌入较强的水印信息.因此，基于HVS模型和相关统计知识，本研究采用FCM算法对图像的局部特征进行模糊聚类，将其划分为两个类：一个类适合嵌入数字水印信息，有较强的透明性和鲁棒性；另一个类则不适合嵌入数字水印.

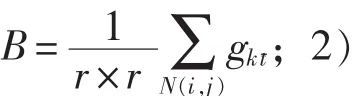
4.2 数字水印的嵌入

设宿主图像H和二值水印W的大小分别为M×M和N×N，则水印嵌入步骤如下.

1）首先对W进行Arnold置乱得W′，迭代次数K作为检测水印的密钥，然后用zigzag算法将水印图像W′映射为一维矩阵w.

2）将宿主图像H划分为大小是r×r的不重叠的块，并对各个块从1开始依次进行编号.

3）先由下文4.1节方法获取适于嵌入水印的图像子块，然后根据块号，按从小到大的顺序将水印信息嵌入到各个被确定的块中，直到所有水印信号嵌入完成为止.其中，一个块被嵌入1 bit水印信息.下面给出将1 bit水印信息w（k）嵌入到一个块L中的过程.

① 对L进行SVD变换，并用下式对其最大奇异值λ1进行量化以嵌入水印信息w（k）：

式（7）中，floor（）为取整运算符，Δ为量化步长，γ∈（0，1）， k=1，…，N × N. 实验表明当Δ∈[40，70]及γ=0.25时，水印算法具有较好的鲁棒性和不可感知性.

② 进行逆SVD变换，可得含水印信息的L′.

重复上述过程，将所有水印信号嵌入到相应的图像子块中，然后用这些含有水印信息的子块代替原有的子块并结合未修改的图像子块，便可以得到含水印图像H′.保存被嵌入了水印信息的子块的编号作为检测水印的辅助信息.

4）计算水印图像H′的Zernike矩A00、A11、A22和A51，并以其作为水印检测过程检测图像几何失真参数的辅助信息.

4.3 数字水印的提取

本研究讨论的数字水印算法在检测数字水印时不需要原始的载体图像，但需要用到原始水印图像的Zernike矩A00、A11、A22和A51作为几何校正的辅助信息.水印检测过程中，先对待检测图像Hw进行几何失真检测，若Hw被几何攻击，则对其进行几何校正后再提取水印；否则直接提取水印.具体步骤如下：

1）根据第1节的几何校准算法对Hw依次进行翻转、缩放、旋转和旋转-缩放组合攻击检测.若成功检测出其中一种攻击（如旋转），则检测过程结束，并令Hw表示校正图像；

2）将Hw划分为大小是r×r的不重叠的块，并根据被嵌入水印的块的编号取出相应的图像子块；

3）根据块号，按从小到大次序从各个块中提取水印信息.下面给出从一个块中提取出水印信息w（k）′的过程，对该块进行SVD变换，并根据下式提取w（k）′，

式中，rem（）为求余运算符，λ1′为该块的最大奇异值.重复上述过程，检测出所有水印信息；

4）先对w′进行逆zigzag变换得w″，然后用密钥K对w″进行逆Arnold变换得提取水印W′.

5 实验结果与分析

本研究采用Matlab对所提水印算法进行仿真实验.为了验证水印算法的有效性，选取大小为512×512的标准灰度测试图像Barbara、Camion和Pentagon作为宿主图像以及大小为32×32的二值图像作为水印图像进行测试，如图1所示.实验中，对宿主图像分块，分块大小为8×8，K为90，量化步长为50.另外，采用峰值信噪比[6]衡量了原始图像与含水印图像之间的差别，采用归一化相关系数[6]定量分析了提取水印与原始水印的相似度.当峰值信噪比大于30 db时，认为含水印图像与原始图像不存在视觉上的差别[11]；当归一化相关系数大于0.7时，认为所提取的水印图像是有效的[11].

图1 宿主图像及原始水印

图2 为未受任何攻击时的结果，其中（a）、（c）及（e）是水印图像，它们的峰值信噪比分别为 40.82 db、 41.33 db和 40.47 db； 而（b）、（d）及（f）则是相应的提取水印， 其归一化相关系数值均为1.由图1和图2可知，在未受攻击的情况下，嵌入水印后的图像与宿主图像在视觉上几乎没有差别，具有很好的透明性.

图2 未受任何攻击的实验图

表1 宿主图像的聚类结果

为验证FCM算法对水印算法的影响，分别对每幅宿主图像进行50次FCM实验，并求出平均迭代次数和收敛时目标函数的值，结果见表1.以图Barbara为例，其每一次的迭代次数与平均迭代次数的差值都不大，且都收敛于相同的目标函数值，即没有陷入局部最优，聚类正确收敛.同时，实验结果指出迭代次数对于所提算法几乎没有影响，同一幅图像在每次聚类后得到的峰值信噪比基本一致.

为了检测本文算法的鲁棒性，分别对含水印图像进行抗几何攻击和抗常见攻击测试.

5.1 抗几何攻击测试

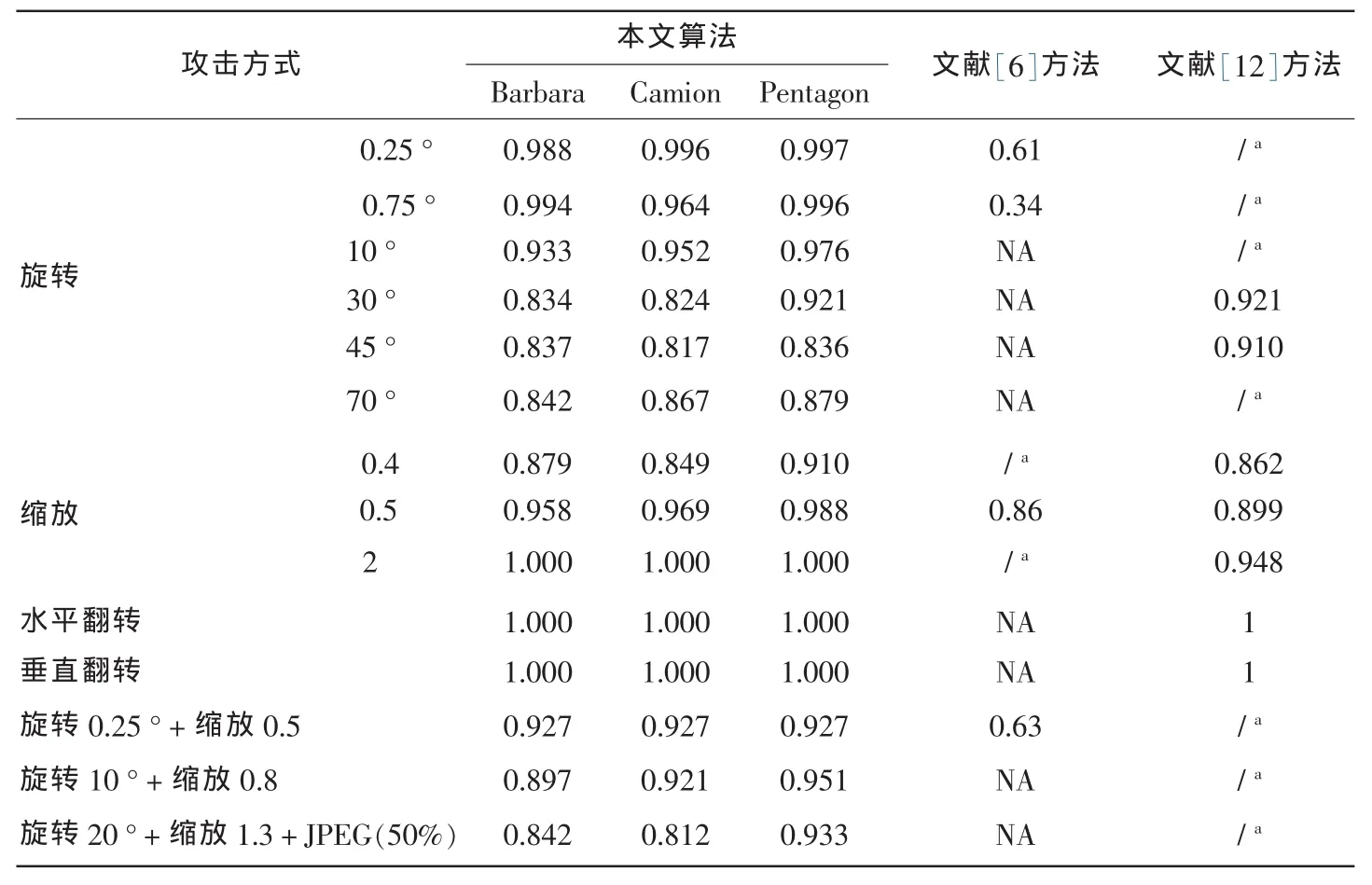
表2 几何攻击后提取水印的归一化相关系数

图3 部分几何攻击后的提取水印

先对含水印图像分别进行翻转、旋转、缩放和旋转-缩放组合等几何操作，然后对失真图像进行几何校正，最后检测水印.表2给出实验结果，并与文献［6］和文献［12］进行了对比，图3为部分几何攻击的实验结果.由表2和图3可知，本文算法对翻转攻击有很强的抵抗能力，对任意角度的旋转攻击以及缩放因子大于0.3的缩放攻击也有较强的鲁棒性，并能有效地抵抗旋转-缩放组合攻击.与文献［6］方法相比，本文算法具有更好的抗几何攻击的性能；文献［12］虽具有较佳的抵抗旋转攻击的能力，但抗缩放攻击的性能不如本文算法.因为基于Zernike矩的图像几何校准算法不能有效地检测灰度图像的平移失真参数，所以本文算法不能有效抵抗平移攻击，此为不足之处.

5.2 抗常见攻击测试

为了验证该算法对常见攻击的鲁棒性，对图像作JPEG压缩、滤波、叠加噪声和图像增强等常见图像处理，然后进行水印检测.实验结果见表3，并与文献［6］和文献［3］进行了对比，图4为相应的提取水印.从表3和图4可以看出，本文算法对JPEG压缩、滤波和图像增强等攻击具有较强的鲁棒性，并由结果比较可知，本算法抗JPEG压缩、低通滤波和叠加噪声等攻击的性能优于文献［6］和文献［3］.

表3 常见攻击后提取水印的归一化相关系数

图4 常见攻击后的提取水印

6 结 语

结合HVS的感知特性与图像的局部相关特性，本研究提出一种基于模糊聚类分析和Zernike矩的自适应图像水印算法，且在水印提取过程中不需要原始载体图像.该算法具有以下特点：1）与传统的基于聚类技术的水印算法相比，具有更好的抗几何攻击的性能；2）综合考虑影响水印嵌入的多种因素，并应用模糊C-均值聚类算法实现水印嵌入位置的自适应选择，从而具有较好的透明性；3）良好的透明性较有效地解决数字水印透明性和鲁棒性之间的矛盾.未来的研究工作为改进基于Zernike矩的图像几何校正算法，以有效检测平移失真参数，从而提高水印算法抗平移攻击的鲁棒性.

[1]王向阳，杨红颖，赵红，等.基于模糊聚类分析的自适应图像空间域水印技术[J].小型微型计算机系统， 2005， 26（7）： 1 255-1 258.

[2]吴健珍，谢剑英.基于模糊聚类和HVS的DWT自适应盲水印算法研究[J].计算机工程与应用，2004， 17： 109-111.

[3]朱映辉，江玉珍，杨群生.基于小波变换和FCM分析的盲水印算法[J].计算机工程，2008，34（13）： 136-138.

[4]Chen Weiche,Wang Mingshi.A fuzzy c-means clustering-based fragile watermarking scheme for image authentication[J].Expert Systems with Applications， 2009（36）： 1 300-1 307.

[5]Wang Mingshi，Chen Weiche. A hybrid DWT-SVD copyright protection scheme based on k-means clustering and visual cryptography[J].Computer Standards&Interfaces， 2009（31）： 757-762.

[6]Lin Weihung， Wang Yuhrau， Horng Shijinn.A wavelet-tree-based watermarking method using distance vector of binary cluster[J].Expert Systems with Applications， 2009（36）： 9 869-9 878.

[7]李雷达，郭宝龙.基于伪Zernike矩的图像自适应RST不变水印[J].西安电子科技大学学报（自然科学版）， 2007， 34（1）： 38-42.

[8]Khotanzad A，Hong Y H.Invariant image recognition by Zernike moments[J].IEEE Trans On Patter Analysis and Machine Intelligence， 1990（12）： 489-497.

[9]Ahmad A， Mohammad， Ali Alhaj， et al.An improved SVD-based watermarking scheme for protecting rightful ownership[J].Signal Processing， 2008（88）： 2 158-2 180.

[10]张伟.数字水印中FCM算法的应用研究[J].计算机科学，2002，29（8）：117-118.

[11]Chang Chinchen， Hu Yihshin， Lu Tzuchuen.A watermarking-based image ownership and tampering authentication scheme[J].Pattern Recognition Letters， 2006（27）： 439-446.

[12]Chen Jie， Yao Hongxun， Gao Wen， et al.A robust watermarking method based on wavelet and Zernike transform[C]//ISCAS， 2004： 173-176.

Abstract：An adaptive geometric robust watermarking scheme is presented based on fuzzy clustering and Zernike moments technique.By utilizing fuzzy C-mean clustering algorithm and human visual system，the suitable locations for embedding watermark are selected adaptively.The watermark is embedded into the host image by singular value decomposition transform.In the watermark detection process,the geometric distortion parameters of the attacked image are estimated first by the geometric correction method whichis based on the Zernike moments.The watermark is extracted from the recovered image.The experimental results demonstrate that the proposed scheme is invisible and robust against rotation,scaling， flipping and combined attacks， as well as a variety of common manipulations such as JPEG compression,filtering，cropping and image enhancement.

Key words：adaptive watermarking algorithm；fuzzy C-means clustering；Zernike moments；geometric attacks

Adaptive Watermarking Algorithm Based on Fuzzy Clustering and Zernike Moments

YU Chu-ying1， LI Jian-zhong2， ZHANG Bo-quan3

（1.Department of Physics， Shantou University， Shantou 515063， Guangdong， China；2.Department of Mathematics and Information Technology， Hanshan Normal University， Chaozhou 521041,Guangdong， China； 3.Faculty of computer， Guangdong University of Technology， Guangzhou 510006， Guangdong，China）

TP 391

A

1001-4217（2010）04-0066-09

2010-06-03

余楚迎（1974－），女，广东汕头人，高级实验师.研究方向：数字图像处理.

*通讯联系人E-mail：henry_stu@163.com