具有大形变特征的颅脑CT图像的非刚性配准
2010-09-11峰刘伟李传富2冯焕清
徐 峰刘 伟李传富,2冯焕清*
1(中国科学技术大学电子科技系,合肥 230027)2(安徽中医学院第一附属医院影像中心,合肥 230031)
具有大形变特征的颅脑CT图像的非刚性配准
徐 峰1刘 伟1李传富1,2冯焕清1*
1(中国科学技术大学电子科技系,合肥 230027)2(安徽中医学院第一附属医院影像中心,合肥 230031)
Demons算法是一种基于光流场模型的小形变非刚性配准算法,大形变情况下不具有拓扑保持性,将它用于颅脑CT图像配准时效果不理想。为此,本研究对它进行了改进。首先建立Demons算法目标能量函数,将形变场求解转化为目标函数优化问题;然后通过增加sKL距离作为正则项来优化目标函数,消除了形变场的不适定性,并使形变场更加光滑。对高分辨率颅脑CT图像的实验结果表明,改进算法不仅能够处理大形变问题,还能在处理大形变时通过光滑的形变场得到更精确的配准结果。
医学图像配准;Demons算法;拓扑保持性;Jacobian行列式;sKL距离
Abstract:Demons is a non-rigid image registration algorithm which is derived by assuming small deformations.One of the limitations of the original Demons is that it can not produce topology preserving maps for the large deformations.Aiming to solve this problem,an improved Demons algorithm was proposed in this paper.First,the equation of force in the original Demons was regarded as the result of minimizing the energy function.Then,Demons algorithm was improved by adding a regularization term into the function.The symmetric Kullback-Leibler(sKL)distance in information theory was used as the regularization term.The experiment results with high resolution CT cerebral images demonstrated that the improved algorithm could not only handle large deformations,but also obtain more accurate registration results using smooth deformation fields.
Key words:medicalimage registration;Demonsalgorithm;topology preservation;Jacobian matrix;sKL distance
引言
随着医学影像辅助诊断在临床上的广泛应用,各种医学图像处理技术都得到了深入研究,其中图像配准技术是研究热点之一。图像配准的本质是寻找一种几何变换使得待分析图像和参考图像达到空间位置上的对齐,已应用于图像分割[1]、图像融合[2]、病变检出[3]等诸多方面。医学图像配准方法可分为刚性配准和非刚性配准两大类,其中刚性配准属于全局配准的方法,一般只是对图像的旋转、平移、缩放等几个参数进行仿射变换,达到两幅图像在大体位置上的对齐,常用于相同个体不同次检查或不同模式检查数据之间的配准。而非刚性配准主要应用于异体配准 (inter-subject registration),由于异体配准在统计图谱的建立、病变检出等方面具有重要的意义,因此非刚性配准方法是医学图像配准研究的重点。
非刚性配准算法可以分为两类:模型驱动算法和灰度驱动算法。Demons算法是一种灰度驱动的算法[4]。Hellier等对常用的六种配准算法进行的回顾性对比研究表明,在多种配准精确度评价指标中Demons算法优于其他五种算法[5]。但是 Demons算法只适用于小形变的情况,在出现大形变时Demons算法将不能保持图像的拓扑结构,并产生物理上不合理的形变。然而,在异体配准过程中,由个体之间的生理差异以及占位性病变所导致的大形变问题是不可避免的。因此本研究针对此缺陷改进Demons算法,使其在大形变下具有拓扑保持性,以应用于具有大形变特征的颅脑CT图像的配准。
1 Demons算法原理
Demons非刚性配准算法是 Jean-Philipe Thirion提出的[4],基本思想源于19世纪 Maxwell为了解决热动力学难题而提出的一种实验假设,其假设在参考图像S(x)的目标轮廓上分布着具有选择性的驱动点,由它们驱动待配准图像M(x)上的像素来实现两幅图像的配准。驱动力的形式取自光流场理论方程,而光流场理论的前提是假设图像运动过程中灰度保持不变,即为计算驱动力,将式(1)微分化

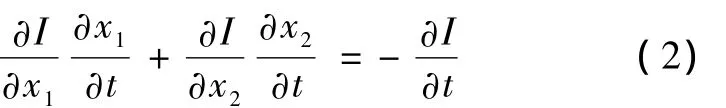
进一步简化式(2)得

其中,x=(x1,x2),S(x)为S(x)的梯度向量,fD为驱动力。从而得到作用力

但是,在参考图像比较均匀一致的区域ΔS(x)→0,式(4)非常不稳定。为解决此问题,对式(4)进行调整,在其分母上增加一个分量,得

2 Demons算法的优化
2.1 配准能量函数构造
图像配准过程就是寻找一个位移场u(x),使待配准图像形变后M(x-u)与参考图像S(x)在某种含义上相似。最通用的相似性测度(能量函数)是L2范数:
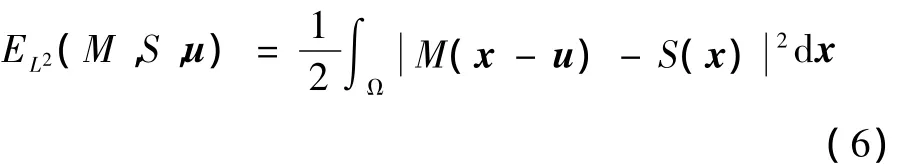
只需最小化式(6),利用梯度下降法求解相应的Euler-Lagrange 方程得到
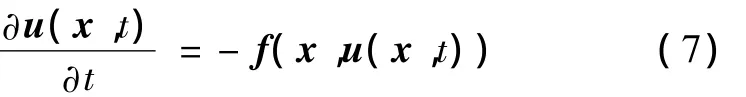
其中,

式(8)即为驱动待配准图像的力场。M|x-u为形变后图像的梯度,它决定了力的方向;M(x-u)-S(x)为两幅图像的灰度差。
这种优化的问题在于其不适定性,尤其是形变场u的不唯一,因此需要对u进行正则化。一般是通过在式(6)中增加正则项来解决[6],则能量函数变为:
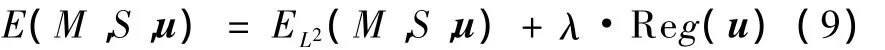
可以看出式(8)与式(5)很相似,因此本研究假设式(5)是最小化相似函数 ED(M,S,u)得到的驱动力场,由上述知需要对解进行正则化。而Thirion原来的Demons只是通过简单的高斯平滑来正则化,这正是 Demons算法局限性的原因所在。像式(9)那样引入正则项来改进Demons算法,所采用的正则项是配准变换的Jacobian行列式分布与恒等变换之间的sKL距离。
2.2 正则项
令待配准图像M(x)到参考图像S(x)的变换为h:M→S,则位移场u(x)与h(x)满足h(x)=x-u(x)。只要变换h满足两个条件就可保持拓扑结构[7]:①变换h的Jacobian行列式为正值;②变换h是一一对应即双射变换。
设Dh为h的Jacobian矩阵相应的 Jacobian行列式为令,则 2D图像变换的Jacobian行列式为
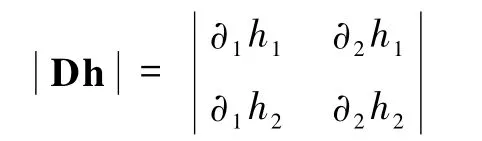
对于二维空间坐标变换,Jacobian行列式的物理含义为说明面积微元膨胀1则收缩面积不变为奇点。当面积微元ds(x)处 Jacobian行列式都等于1时,则变换前后微元ds(x)的面积没有变化,即变换前后是恒等映射,是一一对应的。因此,若正向变换和逆向变换各点的Jacobian行列式分布足够接近恒等映射,就可以满足局部坐标系的拓扑保持性。采用信息论中 symmetric Kullback-Leibler(sKL)距离[8]来衡量这种接近程度。
设X与Y是两概率密度函数,则KL距离为sKL距离定义为

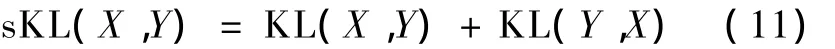
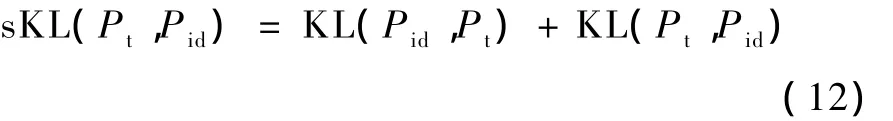
令 h-1为h的逆变换,则满足

对式(13)两边求导并设y=h(x)得所以

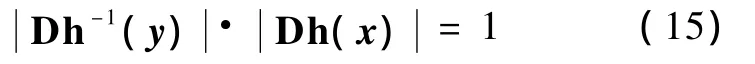
由式(10)与式(15)可以推导得
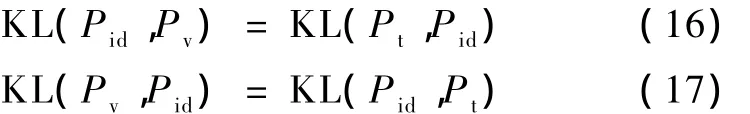
由此可以得到
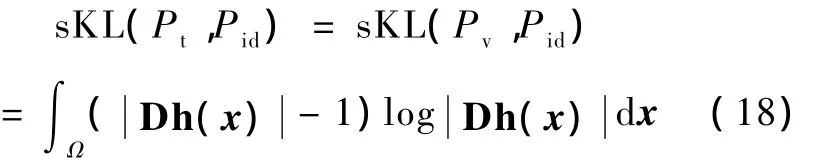
因此,最小化式(18)就使得正向变换与逆向变换的Jacobian行列式分布最接近恒等映射。
这样,由式(9)与式(18)就可得到新的能量函数
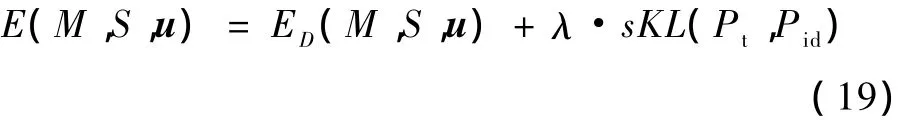
令 u=(u1,u2)及函数L(J)=(J-1)log(J),则驱动力的公式更新为
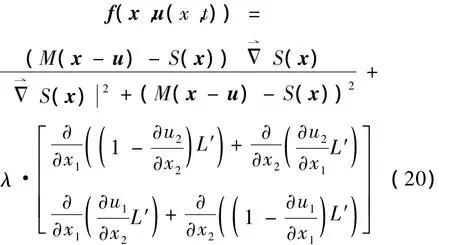
3 算法实现
3.1 双向多分辨率配准策略
为了克服Demons算法因其完全自由变形特点可能导致的空间结构不连续,并增加该算法的鲁棒性,在实现改进算法时采用了双向配准策略[9]。即以M(x)为待配准图像,S(x)为参考图像得到正向的形变矩阵Tf;再以S(x)为待配准图像,M(x)为参考图像得到逆向的形变矩阵 Tr。最后 M(x)向S(x)配准的形变矩阵T为Tr与Tf的均值,由于Tr与Tf的方向相反,得出T=(Tf-Tr)/2。
多分辨率配准策略就是从粗到精的分级配准。较低分辨率的图像更能反映图像的轮廓特征并且更加稳定,高分辨率图像配准是在低分辨率配准结果的基础上进行的,因此采用多分辨率配准策略不仅可以显著提高算法的运算速度,而且能够达到更精确的配准效果。
3.2 形变场叠加
在配准过程中,每次迭代都是以上次迭代的结果为待配准图像,即 Mi+1=Ti°Mi,其中 Mi为第 i次迭代的待配准图像,Ti为第i次迭代的形变场,Mi+1为第i次迭代的配准结果,同时也是第i+1次的待配准图像。所以要进行多次Ti°Mi插值操作,这会导致配准后图像细节丢失和模糊。
本研究通过将形变场叠加来解决这一问题,即将多次形变场Ti合并为T,再进行一次T°M0操作得到配准结果,具体的叠加方法如图1所示。

图1 形变场叠加Fig.1 Deformation fields stacking
待配准图像Mi经两次形变得到配准结果Mi+2=Ti+1°(Ti°Mi)。所以只需要知道 Ti(p)和Ti+1(p),就可以得到从Mi中p位置到Mi+2中p位置的形变T(p)=Ti(p)+Ti+1(p)。而Ti只是已知整数坐标点的形变,因此需要通过插值来得到非整数坐标点的形变,采用双线性插值方法来计算图1中的形变 Ti+1(p)。
3.3 实现步骤
改进算法的具体步骤如下:
初始化:u(x,0)=0;
步骤1:按式(20)计算出待配准图像M(x)每一个 Demons点的力 f(x,u(x,t));
步骤2:根据力 f(x,u(x,t))和 Demons算法的参数项力衰减系数α,计算出形变的位移场u(x,t)= α·f(x,u(x,t));
步骤3:将位移场 u(x,t)与高斯核 Gσ卷积u(x,t)=Gσ*u(x,t),将位移场 u(x,t)应用于待配准图像M(x)使其形变,得到M(x-u);
步骤4:若式(19)能量函数的值与前一次迭代的值之间的差小于某阈值则停止,否则返回步骤1。
4 实验结果及讨论
采用512像素×512像素的高分辨率颅脑 CT图像来比较 Demons算法与本改进算法的配准性能。Demons算法是文献[9]优化后的 Demons算法,并采用该文献提供的参数。在实现改进算法时采用了双向配准和多分辨率策略。图2中(a)和(b)分别为待配准图像与参考图像,两幅图像来源于不同个体的同一层片,且已去除了颅骨和支架。图2中(c)和(d)分别为Demons算法与改进算法的配准结果,均进行了3次迭代,其中改进算法式(20)中的参数λ取λ=1.2。
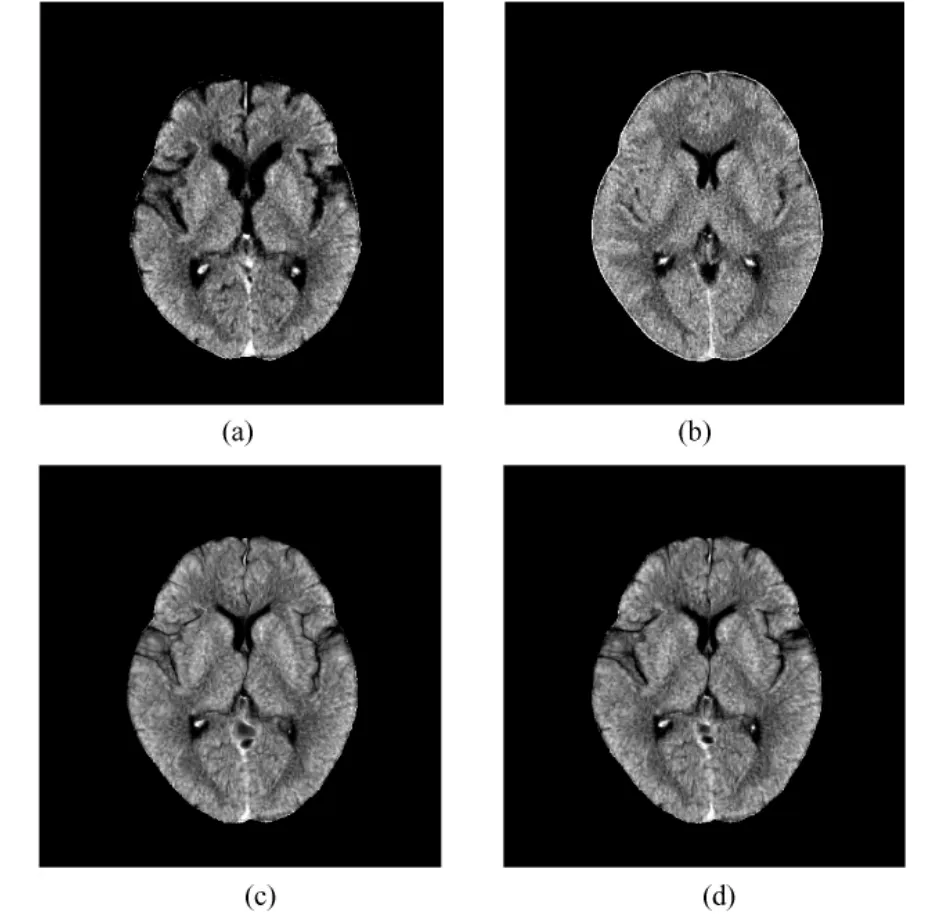
图2 CT图像配准。(a)待配准图像;(b)参考图像;(c)Demons配准结果;(d)改进算法配准结果Fig.2 CT image registration.(a)template image;(b)reference image;(c)registration result of Demons;(d)registration result of proposed algorithm

图3 配准结果与参考图像的差值图像。(a)Demons算法;(b)改进算法Fig.3 Differencebetween registration resultand reference image.(a)Demons;(b)proposed algorithm
由图2中(c)和(d)可以看到两种方法都得到了精确的配准结果,从图3的差值图像也可以看出两种方法的结果都比较精确。图4是将两种方法的形变场施加于网格得到的结果,通过对比图4的(a)和(b)中圆圈标记处的网格,可明显看出改进算法的网格更加规则,这说明改进算法有更加平滑的形变;而Demons算法的网格在某些区域出现了严重的弯曲,甚至几乎交叉折叠。这是因为在这些区域有Jacobian行列式为负的情况,表明拓扑结构发生了变化。可见,由于获得了更加平滑的形变场,改进算法得到的结果更精确。也就是说,在大形变的情况下,该算法能更好地保持图像的拓扑结构。
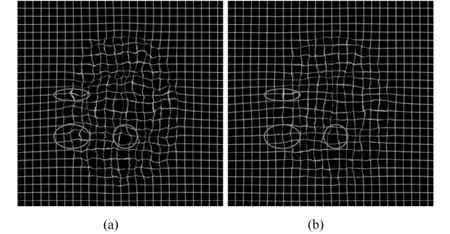
图4 形变场网格对比图。(a)Demons算法;(b)改进算法Fig.4 Deformed grids Comparison.(a)Demons;(b)proposed algorithm
图5为两种方法在3次迭代中颅脑区域内Jacobian行列式的统计直方图,其中图5(a)、(c)、(e)为Demons算法的结果,图 5(b)、(d)、(f)为改进算法的结果。很明显,本算法的Jacobian行列式统计分布更加尖锐,Jacobian行列式更集中于1附近,这也说明改进算法具有更加平滑的形变。从图6(图5(c)的放大图)中的标记处可以看到,Demons算法有少量的Jacobian行列式为负值,这正是图4(a)中Demons网格出现严重弯曲的原因。这说明了Demons算法在大形变的情况下改变了拓扑结构,而改进算法得到了很好的结果。图7是两种方法第一次迭代后形变的拓扑改变程度图(其他迭代的结果类似),可以看到本算法的结果明显地优于原Demons算法的结果。
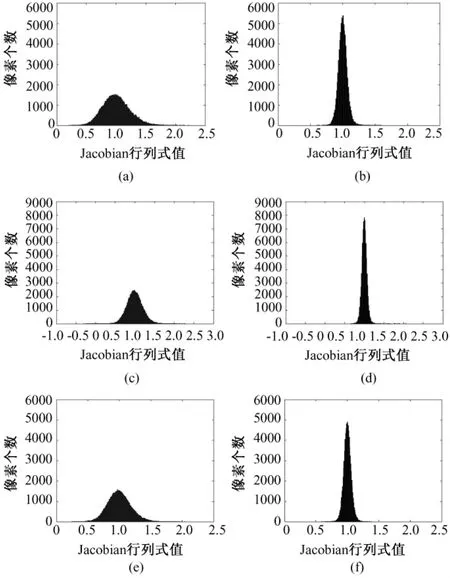
图5 颅脑区域内Jacobian行列式统计直方图。(a)和(b)Demons和改进算法第1次迭代;(c)和(d)Demons和改进算法第2次迭代;(e)和(f)Demons和改进算法第3次迭代Fig.5 Histograms of Jacobian values of deformations inside brain.(a)and(b)the first iteration of Demons and the proposed algorithm;(c)and(d)the second iteration of Demons and the proposed algorithm;(e)and(f)the third iteration of Demons and the proposed algorithm
图8(a)是一幅具有占位性病变的CT图像,图8(b)是图8(a)(待配准配准图像)向图2(b)(参考图像)配准的结果,图9(a)(b)分别是两种方法第一次迭代中颅脑区域内Jacobian行列式统计直方图(另外两次迭代结果与之相似),从图9(a)中可看出原 Demons算法仍存在Jacobian行列式为负值的情况,而改进算法仍然得到很好的结果,这说明改进算法适用于由占位性病变引起的大形变问题。

图6 图5(c)的放大图Fig.6 Larger image of Fig.5(c)

图7 拓扑改变程度图。(a)Demons算法;(b)改进算法Fig.7 Topology change images.(a)Demons;(b)the proposed algorithm

图8 占位性病变图配准结果。(a)待配准图像;(b)配准结果Fig.8 CT image with occupying lesionsand result of registration.(a) template image;(b) result of registration
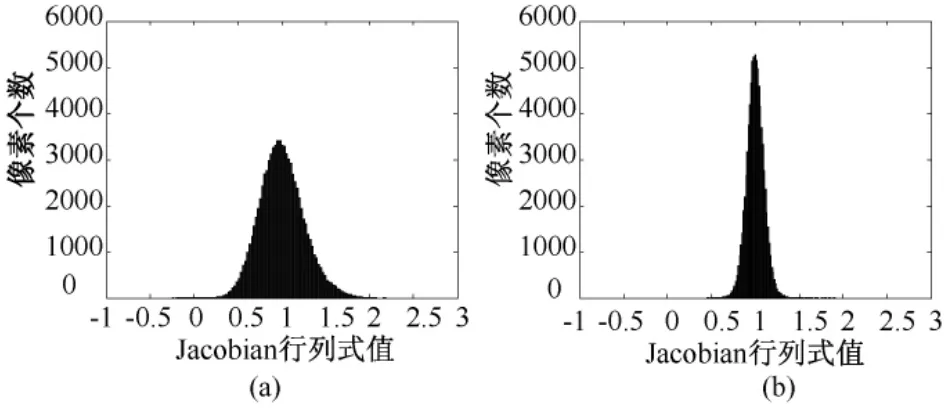
图9 颅脑区域内Jacobian行列式统计直方图。(a)Demons算法;(b)改进算法Fig.9 Histograms of Jacobian values of deformations inside brain.(a)Demons;(b)proposed algorithm
5 结论
Demons算法是在假设小形变的前提下由光流场原理推导出的方程,因此在处理不适用于Demons算法的大形变问题时,拓扑结构不能得以保持,故本研究对 Demons算法进行了改进。先将 Demons算法中的驱动力方程看作是极值化能量函数的结果,再通过引入Jacobian行列式统计分布与恒等变换之间的sKL距离来更新能量函数,得到新的驱动力方程,从而实现了改进。改进算法实现时采用了双向配准和多分辨率策略。用高分辨率颅脑CT图像数据的实验结果表明,改进算法在处理大形变时具有良好的拓扑保持性,并得到了比Demons更精确的配准结果,将被应用到基于HRCT图像的脑部病变计算机辅助诊断系统设计中。
[1]Pitiot A,Delingette H,Thompson PM,et al.Expert knowledgeguided segmentation system for brain MRI[J].NeuroImage,2004,23(1):S85-S96.
[2]Pietrzyk U,Herholz K,Schuster A,et al.Clinical applications of registration and fusion of multimodality brain images from PET,SPECT,CT,andMRI[J].EuropeanJournalof Radiology,1996,21(3):174-182.
[3]Lee JM,Kim SH,Jang DP,et al.Deformable model with surface registration for hippocampal shape deformity analysis in schizophrenia[J].NeuroImage,2004,22(2):831-840.
[4]Thirion JP.Non-rigid matching using demons[A].In:Computer Vision andPatternRecognition(CVPR '96)[C].San Francisco:IEEE,1996.245-251.
[5]Hellier P,Barillot C,Corouge I,et al.Retrospective evaluation of intersubject brain registration.Medical Imaging[J].IEEE Transactions on Medical Imaging,2003,22(9):1120 –1130.
[6]Vercauteren T,Pennec X,Perchant A,et al.Non-parameteric Diffeomorphic Image Registration with the Demons Algorithm[J].MICCAI2007,Part II.LNCS,2007,4792:319 – 326.
[7]Holden M.A review of geometric transformations for nonrigid body registration[J].IEEE Transactions on Medical Imaging,2008,27(1):111–128.
[8]Yanovsky I,Thompson PM,Osher S,et al.Topology preserving log-unbiased nonlinear image registration: theory and implementation[A].In:Computer Vision and Pattern Recognition[C].Minneapolis:IEEE,2007.1-8.
[9]李传富.颅脑CT病变的计算机自动化检出方法研究[D].合肥:中国科学技术大学,2005.
A Non-rigid Registration of the Cerebral CT Images with Large Deformations
XU Feng1LIU Wei1LI Chuan-Fu1,2FENG Huan-Qing1
*1(Department of Electronic Science and Technology,University of Science and Technology of China,Hefei 230027,China)2(Medical Imaging Center,First Affiliated Hospital of Anhui Traditional Chinese Medicine College,Hefei 230031,China)
R319
A
0258-8021(2010)02-0172-06
10.3969/j.issn.0258-8021.2010.02.003
2009-06-19,
2009-11-11
国家自然科学基金资助项目(60771007)
*通讯作者。 E-mail:hqfeng@ustc.edu.cn
