利用生物声纳中双耳多普勒效应探讨定量神经编码
2010-09-11钱鸣奇覃曦刘淑芳张宏童勤业
钱鸣奇覃 曦刘淑芳张 宏童勤业,3*
1(浙江大学生物医学工程教育部重点实验室,杭州 310027)2(浙江大学生物医学工程系,杭州 310027)3(浙江大学神经信息学中心,杭州 310027)
利用生物声纳中双耳多普勒效应探讨定量神经编码
钱鸣奇1,2覃 曦2,3刘淑芳2,3张 宏1,2童勤业1,2,3*
1(浙江大学生物医学工程教育部重点实验室,杭州 310027)2(浙江大学生物医学工程系,杭州 310027)3(浙江大学神经信息学中心,杭州 310027)
为了探讨不稳定的生物神经系统检测变化信号的方法,以及变化信号与神经系统输出脉冲的定量关系,本研究基于神经元模型(H-H方程),用计算机仿真研究生物声纳对双耳多普勒效应的处理机制。双耳多普勒效应差可以确定运动物体的运动方向,由于双耳检测到的频率差别非常小,因此神经系统必须具有很高的信号分辨能力。本研究的仿真分析结果,证明神经系统存在高灵敏地区分多普勒信号的可能性,讨论了神经系统实现“定量”处理的可能性。
多普勒效应;生物声纳;神经编码;序空间;圆映射
Abstract:To investigate the method to measure the variable signals by the unstable nervous system,and the quantitive relation between the variable signals and the output spikes of the nervous system,this paper studies the binaural doppler effect processing model of biosonar based on H-H equations and computer simulation.Movement orientation of object can be detected using difference of doppler effect between two ears.Because of the frequency difference caused by binaural Doppler effect is very small,which calls for the nervous system must have the high-sensitivity(resolving power).According to the simulating results,it seemed that there was indeed possible to achieve high-sensitivity distinction small change of signal.The possibility that information processing in neural system was quantitative was discussed.
Key words:Doppler;biosonar;neural code;ordered space;circle mapping
引言
多年来人们一直在研究海豚、蝙蝠等声纳系统如何来校正由多普勒效应所引起的测量误差,像多普勒容限(Doppler tolerance)、多普勒关联误差(Doppler-related error)、多普勒关联测距误差(Doppler-related ranging error)等概念相继被提出[1-3],这些研究虽然包含多种实验,但至今依然为某种猜测。McCarty的研究结果说明蝙蝠对运动物体的检测比静止目标更有效[4],文献[1]的研究也支持生物声纳系统能处理多普勒效应的信号。更为重要的是,生物体用于处理多普勒信号的神经系统是很不稳定的系统,一个不稳定系统是否可以或者如何高灵敏地检测由目标物低速移动所产生的约0.05 Hz的多普勒频偏信号。本研究以多普勒测量为例,分析了生物神经系统中可能存在的对多普勒效应更精细的利用。不仅可能快速处理多普勒信号,而且其灵敏度很高,能精细地测量多普勒效应。
1 材料与方法
1.1 双耳多普勒效应
由于运动物体所产生的多普勒效应对于两耳不对称,动物的双侧听觉器官若出现多普勒效应差,即双耳多普勒效应。
双耳多普勒效应可以分为主动和被动两种。主动多普勒效应是蝙蝠发出声音,声音到达目标飞行物再反射回来,由于目标物在飞行中,相对到两耳的速度不同,这就产生多普勒效应差。这种差别,就是主动双耳多普勒效应。如果蝙蝠本身不发出声音。只要目标飞行物发出声音,也构成双耳多普勒效应。称为被动双耳多普勒效应。如果只考虑双耳多普勒效应,则主动和被动是一样的。图1所示为分析蝙蝠的双耳多普勒效应的原理图。

图1 双耳多普勒效应原理图(L和R分别代表蝙蝠左、右两耳;B是目标声源(飞行物,如小虫))Fig.1 Illustration of binaural Doppler effects.(L and R represent left and right ear of a bat,respectively;B represent a target)
单一声道Doppler效应按式(1)计算

式中,f0为声源B的发射频率;U为声音在介质中传播速度,假定在空气中传播速度=340 m/s;V1为声源B(飞行物)运动速度;α1为声源与接受器连线LB与V1运动方向的夹角;V2为接受器(耳)(R和L)运动速度;α2为声源与接受器L连线LB与V2运动方向的夹角。
按式(1)可求出双耳多普勒效应差

式中,γ是蝙蝠飞行方向角,β1、β2分别表示飞行物位置方向和飞行物运动方向角。
γ=90°,说明蝙蝠飞行方向是沿着头部正前方。此时,m1=m2.式(2)就成为

1)在上述条件下同时有 β2=90°时,说明飞行物朝着蝙蝠正方向飞来,此时,Δf=0,表明两耳的多普勒效应差为零;
2)当 β2=0时,式(3)成为

此时Δf正负就可以确定飞行物向左还是向右飞行。飞行物运动速度V1越大Δf也越大。m1越小表明目标物距离远,Δf也越小。当M1趋向于零,表明飞行物在无穷远。Δf也趋向零。这表明在很远处两耳多普勒效应差为零。
1.2 双耳多普勒的频差
双耳多普勒效应的利用还取决于其两耳多普勒的频差Δf的大小,以及其神经系统能否达到这样高的分辨率。
自然界中飞行最快的昆虫——蜻蜓的飞行速度约在27.8~41 m/s,而一般的昆虫飞行速度约在3 m/s左右,蝇的飞行速度大约在 2.7 m/s[5],而空气中的声速为340 m/s。
假定昆虫的飞行速度是V1=3 m/s,距离OB=λ=2~5 m,取2 m。声音频率 f0=500 Hz。蝙蝠两耳距离30 mm,蝙蝠飞行速度V2=5 m/s

根据以上参数,式(4)为

对于水中海豚也可作同样分析,假定海豚发出的声音频率 f0为500 Hz,海豚的最快游动速度约11.111 m/s,假定为V2=1 m/s;食物(小鱼)瞬时游动速度V1=2 m/s,海豚两耳距离150 mm,食物距离OB=3 m,水中声速 U=1 000 m/s。则在与上例同样条件情况下式(4)为

从式(5)和式(6)两例看出海豚和蝙蝠两耳多普勒频差约在0.05 Hz,也就是说,神经系统需要能达到这样的分辨能力。
1.3 神经系统分辨频率的能力
假定听觉神经系统所输出的脉冲序列的频率与听神经接收的声音信号的频率成单调关系,也即声音频率越高,输出脉冲序列的频率也越高。因此,神经系统对声音频率的处理,在神经回路内就变成为神经脉冲频率的处理。
用脉冲信号作为输入信号,神经元模型的H-H方程如下


如果H-H方程存在圆映射,就可以用符号动力学方法进行分析[9-10]。输入等周期脉冲序列、输出脉冲序列可根据符号动力学的方法变为符号序列,具体方法可详见文献[6,11]。
符号化的规则由式(8)描述,其中的周期格就是图2(a)中ri和ri+1之间的时间段。


图2 神经元输入输出信号的圆映射和广义圆映射示意图(ri为输入信号(刺激),在这里作为圆映射的时间刻度,δi为输出信号,τ和 τi为脉冲之间时间间隔)。(a)圆映射;(b)广义圆映射Fig.2 Illustration of circle map and generalized circle map of the input and output spikes of a neuron.The time scale of circle map riis the input(stimulus)signal;δiis output signal,τ and τiare the interval between the spikes.(a)circle map;(b)generalized circle map
按文献[11]定义两符号序列的距离设两序列A和B分别为
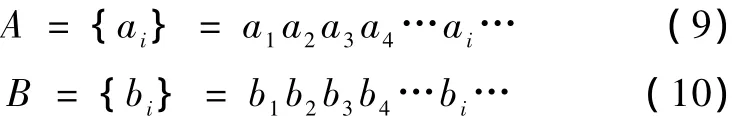
其中 ai=p1,p2,p3,…,pi,…,pr
bi=p1,p2,p3,…,pi,…,pr
定义:两序列A与B的距离
“这有什么大不了的?壶天晓还进过我的记忆库呢!”镜心羽衣哼了一声,说道,“壶天晓,丁达还有实时影像池的功能,这个是做什么用的?”

当 A=B 时,d(A,B)=0
按距离定义,只要符号序列足够长,距离可以小到任意小。符号序列的长度就是脉冲序列的长度。当然在生物神经系统中脉冲序列是不可能无限长的。
1.4 单纯音多普勒频率变化仿真
以单一频率的声波检测多普勒的频率变化,可以简化为神经元对两个频率非常接近的信号的测量。采用式(7)的H-H方程进行仿真,输入信号为Isig,其形式为等周期的脉冲序列,脉冲幅度为20μA/cm2,宽度为1 ms的方波。计算过程中方程的参数与文献[6]相同。
计算结果按文献[7]和文献[8]中取圆映射的方法。
使输入到神经元的脉冲序列的频率变化达0.01 Hz。分别计算不同输入频率下的神经元输出的符号序列。符号序列大小的判别方法详见文献[6,11]。
1.5 变频音的多普勒频率变化仿真
实际上蝙蝠发出的声波或飞行目标物(如小飞虫)发出或反射的声波都不是单纯音,那么对于变频率的声音所产生的多普勒效应,神经回路的响应仍然采用计算机仿真验证为不失一般性,采用频率连续增加和减少的脉冲序列作为输入信号。假定频率变化为正弦函数的最后1/4周期,变化范围为300 Hz,当起始频率为500 Hz时,相应的变化函数为
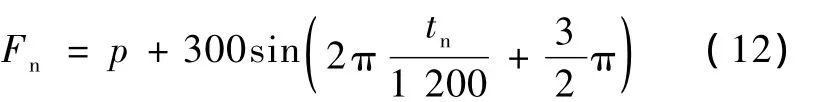
式中,Fn为tn时刻的频率,p为基线频率,取p=800 Hz,tn范围为0~300。当 tn=0时,起始频率 F0=500 Hz,当起始频率加上一个变化量 ΔHz时,则所有 Fn都加上一 ΔHz。
2 结果与分析
2.1 纯音多普勒频率变化仿真结果
图3是一系列不同频率的等周期脉冲序列作用下,神经元所得的系列的映射图。

图3 不同频率的等周期脉冲序列输入条件下的神经元圆映射图。(a)~(o)对应周期1.1~2.5 ms(增加步长为0.1 ms)Fig.3 Neuron circle maps of equal period input spikes with different frequency。(a)~(o)corresponding to the pulse interval(related to the input signal frequency)from 1.1~2.5 ms(step 0.1 ms).
值得注意的是两条函数曲线fL和fR随着频率降低(周期拉长)连续地向右下方移动。当fR移出方格时,原来 fL变成 fR,而新 fL又从左上角出现。其中图3(i)和3(n)中只有很少几个点,这并不说明它们不符合其它各子图的规律,由于作图方法的因素,将一定频率的脉冲序列输入到方程式中,连续计算几千个脉冲,依据混沌轨道的遍历性,画出这一系列的圆映射图,在此格中情况正好出现同步,成为周期解,所以出现了不动点。
当输入到神经元的脉冲序列的频率变化时,不同输入频率下的神经元输出的符号序列见表1,为方便起见,令pi=i,表中7代表p7其他类推。
可简单地把表中符号看作为是21位的十进制的数,数的大小就是符号序列大小。从表中可以看出,随频率增加符号序列也增大。
根据表1中数据来推算分辨出0.1 Hz需要脉冲序列长度为10~20个脉冲。但是由于非线性特性分辨显示不很均匀,频率在505~507 Hz范围,20个脉冲就显得不够了。
从图3可看出,每一小方格中fL和fR随着周期拉长是连续地向左移动,频率变化0.01 Hz,在图3中f1和f2只是移动极小的距离。从符号动力学分析来看,不管f1和f2移动如何小,只要符号序列足够长,总可以把它分辨出来。
从实验数据可见,在499.81 Hz变化到499.85 Hz,符号变化较大,15~16个脉冲就可以看出0.01 Hz的变化。从生物试验观察,10~20个脉冲长度的神经脉冲序列是存在的,也就是说从生物学上是可接受的。从507.08 Hz到507.09 Hz变化时,25个符号仍然无法区别。对于这种情况,序列仿真计算至30个符号以上,问题在于计算精度,现有计算机最大精度是64位双精度。而神经是不稳定系统,计算过程实际上是一迭代过程,误差积累使开始很接近的两轨道随时间延长,最终由于这些误差把参数变化的差别信号全部掩盖,成为同一条轨道,使得求解长轨道失去意义。文中只是说明有可能在较短的脉冲序列中分辨出0.01 Hz的频率变化。真正要减少误差将涉及到高精度微分方程数值解问题,在此不作讨论。
如果这里没有任何计算误差,生物系统确实如计算机仿真的那样工作,这也能说明神经系统只是在某一频率段内短脉冲序列能分辨出0.01 Hz或更小的频率变化。那么蝙蝠在发声时也可调整频率,使声音处在高灵敏的频段内。另外,听觉神经系统中,具有同样功能的细胞是有许多的。每个神经元由于生长情况不同,所以它的参数不完全一样,因此它对频率感受的灵敏频段也是不一样的。把这许许多多感受不同频段的细胞组合起来,就成为一个较宽的频率范围,同样能解决问题。这许许多多细胞的组合也就是Edelman所说的是神经系统“简并性”(Degeneracy)的表现[12-13]。
总而言之,神经系统能区分0.01 Hz的声音频率变化,这就表明神经系统中能分辨出双耳多普勒效应。

表1 输入脉冲序列不同频率与相应的输出的符号序之间的关系Tab.1 Relationship between frequency of the input spike sequence and output symbol sequence
2.2 变频音多普勒频率变化仿真结果
从表2可以看出,变频率的声音多普勒效应也与符号序列呈单调关系,按广义的距离定义[6,11],也可以得出与等周期声音的多普勒一样的效果。

表2 起始频率F0与神经符号动力学序列关系Tab.2 Relations of original frequency F0and neural symbol sequence
3 讨论和结论
本研究是运用确定的微分方程,在计算机上作确定性的推演。结果显示亦为确定性的。但是有一点值得注意。表1和表2中所得的符号序列,是根据神经元存在圆映射而得,而圆映射是从式(7)得到,神经元的可塑性以及不稳定性都会反映在方程的参数变化上,方程参数的任意变化,会影响到方程解的任意变化,具体说,输出神经脉冲序列会任意变,而最终都反映在圆映射图3中fL和 fR两条函数曲线的任意变化,根据符号动力学的理论[10],不管fL和 fR如何变,只要保持原来两函数的单调性,上述分析结果是不变的。这就回答了为什么不稳定系统可高灵敏地检测信号。其实,如果用改进的H-H方程,也能得出上述结果。只要定性上相同的方程都能得到相同结果,同样,H-H方程只要能定性地反映生理状态,则计算结果也能反映生理现象。
本研究实际上是在符号动力学的符号序列空间上分析神经信号过程,文献[1,6,11]把它称为序空间。我们可以从与实空间比较中来理解序空间。众所周知,现代信息科学理论离不开数学,而这些数学都是在实空间中实现的,实数空间可以用笛卡尔坐标表示。笛卡尔坐标是画在刚体上的,序空间是把刚体上的笛卡尔坐标移到弹性体上。例如一维实空间是一条直线,直线上每一点代表一个实数,有其固定的值。如果把这条直线移到弹性体上,这条线任意拉伸,线上每一点都在移动,但是有一点是不变的,这就是各点的相对大小的序是不变的。式(7)中参数任意变化,就相当于不规则的弹性拉伸。因此,有了序空间的概念,就可以理解,为什么不稳定的神经系统可以高灵敏地检测小信号。
由此猜测蝙蝠等生物不仅利用多普勒,而且还可能更精细地利用双耳多普勒效应的差异,来确定目标物运动方向。这为解释蝙蝠定位机制又增加一种信息,进一步证明了不稳定的神经系统存在“精细的”编码或称“定量的”编码的可能性。
需要指出的是,本研究只说明神经系统有极高的分辨率(或称灵敏度),但是没有讨论测量绝对精度,所以研究所讨论的定量,指的是序空间中定量。
本研究是纯理论上的探讨,但根据本研究结果,认为,虽然神经系统内没有标准时钟,神经系统还是有能力对微小的频率变化信号实现高灵敏检测。一个神经脉冲序列的输出,只要到十几个神经脉冲就能够达到0.01 Hz的分辨率。而且时间只需十几毫秒(神经元输出十几脉冲的时间)。脉冲数越多测量分辨率越高,时间略长些,如果可降低分辨率,则检测速度还可提高。也就是说,神经系统是有能力分辨双耳多普勒效应的。从更深层次考虑,只有认识到存在精细或定量编码的机制,才有可能考虑到双耳多普勒效应之类的现象存在。
本研究推断蝙蝠等生物不仅利用多普勒,而且还可能更精细地利用双耳多普勒效应的差异,来确定目标物运动方向,这为解释蝙蝠定位机制又增加一种信息,进一步证明了不稳定的神经系统存在精细的编码或称定量的编码的可能性。
[1]张宏,莫珏,童勤业.海豚的神经系统是如何利用声波定向的?[J].生物物理学报,2007,23(6):455-462.
[2]Holderied MW,Jones G,Helversen Ov,Flight and echolocation behaviour of whiskered bats commuting along ahedgerow:rangedependent sonar signal design,Doppler tolerance and evidence for‘acoustic focusing’[J].The JournalofExperimental Biology,2006,209:1816-1826.
[3]Metzner W,Zhang SY,Smotherman M.Doppler-shift compensation behavior in horseshoe bats revisited:auditory feedback controls both a decrease and an increase in call frequency[J].The Journal of Experimental Biology,2002,205:1607-1616.
[4]McCarty JK,Jen PH-S.Bats reject clutter interference for moving targets more successfully than for stationary ones[J].Journal of Comparative Physiology,1982,152:447-454.
[5]雷仲仁,王音,黄冬如,等,美洲斑潜蝇在不同温度下的飞行能力[J].昆虫学报,2002,45(3):413-415.
[6]张宏,方路平,童勤业.海豚等动物神经系统处理多普勒信号的一种可能性方案[J].物理学报,2007,56(12):7339-7345.
[7]Knudsen EI,KonishiM.Center-surround organization of auditory receptive fields in the owl.[J].Science,1978,202:778-780.
[8]Saberi K,Takahashi Y,Konishi M,et.al:Effects of interaural decorrelation on neural and behavioral detection of spatial cues[J].Neuron,1998,21:789-798.
[9]陈式刚.圆映射[M].上海:上海科技教育出版社,1998.
[10]周作领.符号动力系统[M].上海:上海科技教育出版社,1997.
[11]童勤业,钱鸣奇,李绪,等 嗅觉神经系统脉冲编码的机理研究[J].中国科学 E信息科学,2006,36(4):449-466.
[12]杰拉尔德·埃德尔曼,朱利欧·托诺尼.意识的宇宙[M].上海:上海科学技术出版社,2004.
[13]Edelman GM.Neural Darwinism[M].New York:Basic Book,1987.
Investigation on Quantitative Neural Coding Based on Binaural Doppler Effect in Biosonar
QIAN Ming-Qi1,2QIN Xi2,3LIU Shu-Fang2,3ZHANG Hong1,2TONG Qin-Ye1,2,3
*1(The Key Laboratory of Biomedical Engineering,Ministry of Education,Hangzhou 310027,China)2(Department of Biomedical Engineering,Zhejiang University,Hangzhou 310027,China)3(Neuroinformation Center of Zhejiang University,Hangzhou 310027,China)
Q61
A
0258-8021(2010)02-0195-06
10.3969/j.issn.0258-8021.2010.02.007
2008-09-12,
2009-04-20
国家重点基础研究发展(973)计划(5132103ZZT21B);国家重大基础研究专项基金(2002CCA01800);国家自然科学基金资助项目(60871085)
*通讯作者。 E-mail:bitong@zju.edu.cn
