采用粒子群优化的基因转录差异分析模型

冯伟兴王科俊

(哈尔滨工程大学模式识别与智能系统研究所，哈尔滨 150001)

采用粒子群优化的基因转录差异分析模型

冯伟兴*王科俊

(哈尔滨工程大学模式识别与智能系统研究所，哈尔滨 150001)

高通测序技术可以更加全面地检测实验样本中基因转录水平，这使得对样本间基因转录差异的分析精度越来越准确。根据通过DNA高通测序技术获得的基因转录区内PolⅡ蛋白个数，提出了两个样本间基因转录差异分析模型。该模型在考虑同一基因间转录差异的同时，引入了全基因的转录分布特性以提高模型分析精度。模型采用预测概率最大化统计算法进行参数求取。在概率最大化步骤中，由于难以得到模型参数解析解和提高算法效率，采用粒子群优化算法直接进行求取模型参数数值解。乳腺癌实验数据测试表明，该模型可有效分析不同样本间基因转录差异。

基因;转录差异;粒子群;分析模型

Abstract:Gene transcriptional level in an experiment can be more widely measured with high-throughput sequencing technology，which can obviously improve the analysis accuracy of gene transcriptional change between two experimental samples.Using numbers of PolⅡproteins contained inside each gene transcription region checked with DNA sequencing technology，a novel model was proposed to analyze gene transcription change considering gene transcription levels and the whole genome transcriptional distribution factor as well.Expectation-maximization(EM)statistics algorithm was utilized to resolve the model parameters.For obtaining analytical solution of model parameters and improving the efficiency of algorithm，particle swarm optimization(PSO)was used in maximization step to directly search parameters optimization numerical values.The test to analyze gene transcription change between normal and breast cancer samples verified the effectiveness of the proposed model.

Key words:gene;transcription difference;particle swarm;analysis model

引言

国际基因组测序计划的顺利完成，形成了由几亿个碱基代码组成的DNA序列集，并在其上发现了25 000个以上的人体基因。在此基础上，随着研究的逐步深入，发现在众多调控因子高度非线性的综合调控下，以各种功能蛋白为桥梁，基因间形成着错综复杂的调控关系。一个基因的表达发生变异，就有可能导致整个细胞功能异常，甚至癌病变。因此，在正常和异常两个样本间高精度地分析出表达发生变异的基因，可以为相关疾病诊治提供有意义的参考依据。

随着计算机、控制和信息技术的飞速发展，人们获取细胞样本内基因表达数据的方法越来越成熟［1］。20世纪末出现并逐步发展起来的基因芯片技术，提供了测量样本中基因表达程度的有效方法，基于通过基因芯片技术获得的基因表达数据，Kerr和Wolfinger设计了方差分析模型进行不同样本间基因表达差异测试［2-3］。Dudoit则采用统计学中的T测试法组合比较多样本间的基因表达差异［4］。由于基因芯片仅能做到大体上的全基因表达测量，因此采用简单的统计学方法进行样本间基因表达差异分析是足够的。但随着近几年高通测序技术的出现和成熟，真正意义的全基因表达测量成为可能。与已有的不同样本间基因表达差异分析方法相比，基于高通测序技术，不仅可以参考样本间基因表达测得数据，还可借鉴样本中基因表达的分布特性，从而可以更准确地对基因表达差异进行分析。

相比较而言，DNA高通测序技术已经比较成熟，可用来获取DNA上所结合转录因子、PolⅡ等蛋白信息，该信息因可被用于分析基因前转录调控机制，并间接反映基因表达水平及其基因间调控关系而得到广泛应用［4-7］。在此基础上，RNA高通测序技术也已逐渐成熟。该技术可直接反映基因表达水平并可用于基因变异分析。为了更全面地获取有用信息，相比于一个基因芯片仅能获得几十万条有用信息，目前一次高通测序周期可同时处理30亿个碱基并生成接近1亿条读数。据估计，2009年年底该数字将达到1 000亿个碱基和30亿条读数。面对更加全面的数据，通过设计新方法对其进行有效的生物信息处理，无疑将得到与原有技术相比精度更高的分析成果［8-11］。由于DNA高通测序技术发展得比较成熟，测得数据精度也较高，本文利用该技术测得的数据进行不同样本间基因表达差异分析。具体就是利用DNA高通测序技术测量基因转录区内PolⅡ蛋白数目，进而分析不同样本间基因转录差异。尽管基因转录差异是基因表达差异的有效间接反映，但对于分析不同样本间致病基因及其致病机理仍然具有很大的参考价值。基于此，本文利用DNA高通测序技术测得的数据提出一种分析不同样本间基因转录差异的分析模型，该模型不仅参考样本间基因转录测得数据，还借鉴了样本中基因转录的分布特性。鉴于模型的复杂性，在模型参数的求取过程中采用智能寻优算法。

1 基因转录差异分析模型

在基因转录过程中，PolⅡ蛋白结合在基因转录区内并对基因进行转录，因此，基于基因转录区内PolⅡ蛋白数量可以进行不同样本间基因转录差异分析［12］。

1.1 基因转录数据获取

利用DNA高通测序中的 ChIP-seq技术可以对基因转录区内PolⅡ蛋白数量进行测量和统计，以直接反映基因转录水平。该技术首先利用超声波将DNA链降解为DNA片段，然后利用特制的抗体俘获结合在DNA片段上的PolⅡ蛋白，再利用沉淀技术(IP)将含有抗体的DNA片段滤出，随后通过测序技术(seq)对所有滤出的DNA片段测序并通过序列比对映射回DNA上，最后根据基因转录区在DNA上的位置定义即可实现对基因转录区内PolⅡ蛋白数量的测量和统计［13］。

1.2 基因转录差异分析

在两个样本之间，例如正常样本和癌症样本，为了分析各个基因的转录是否发生变化以及变化程度，这里分为基因转录变化和基因转录不变化两类。然后，依据不同样本中分布在各基因转录区内PolⅡ蛋白的个数及其个数变化程度来判断各个基因属于哪一类以及隶属程度。为此，提出基因转录模型及其转录差异模型并对此进行分析。

1.2.1 基因转录模型

由于细胞中对全部n个基因的调控强度不同，因此一个PolⅡ蛋白结合在不同基因转录区内以对其进行转录的概率是不同的，设该概率为Pi(i=1，…，n)。假设细胞中PolⅡ蛋白的个数处于较低的水平，设其个数为m，则在第i个基因的转录区内结合k个PolⅡ蛋白的概率可用二项分布表示:

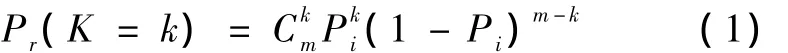
按照这一概率分布，随着细胞中PolⅡ蛋白的个数增多，结合在各基因转录区内的PolⅡ蛋白个数将随之增加。但随着细胞中PolⅡ蛋白的个数继续增多，由于基因转录区上可容纳的PolⅡ蛋白的个数有限，新的PolⅡ蛋白结合在基因转录区内的概率将随之下降，最终，基因转录区内结合的PolⅡ蛋白个数将出现饱和，即mPi(i=1，…，n)将保持不变。事实上，为了保证正常生理功能，细胞中PolⅡ蛋白的个数多处于饱和状态。此时，各基因转录区内结合PolⅡ蛋白的个数应遵循泊松分布:

式中，yi，j是第 j(j=1，2)个样本中第 i个基因转录区内结合 Pol Ⅱ蛋白的个数，而λi，j=mjPi，j为分布常数。按照泊松分布特性，实际测量的PolⅡ蛋白个数 yi，j是基因 i在样本 j中实际转录程度 λi，j的表象，但如何通过 yi，j准确 计算出 λi，j，仅依靠yi，j是无法做到的。此外，即使计算出 λi，j，如何评估其样本间变化程度也是很困难的。一个基因转录从100变为500和另一个基因转录从1 000变为5 000，其表示的转录差异程度是不同的，前者更剧烈一些。为此，结合样本中所有基因的表达分布特性，设计了基因转录差异模型分析样本间基因的转录差异及其差异程度。

1.2.2 基因转录差异模型

据Newton实验分析，在同一样本中，所有基因的表达水平将遵循伽玛分布［14～15］。基于此，可认为:同一样本内，基因转录实际值 λi(i=1，…，n)应遵循伽玛分布:

其中，α，β为模型常数。

两个样本之间，如果第i个基因的转录未发生变化，则在两个样本PolⅡ总数归一化前提下，其在两个样本内均遵循同一伽玛分布，即:

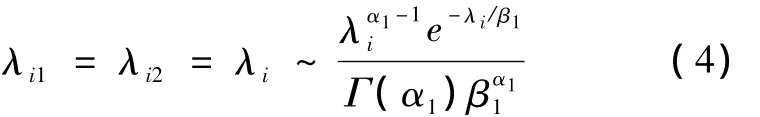
否则:

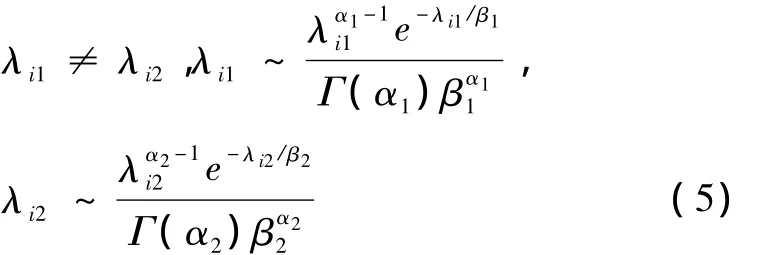
为了计算基因转录差异程度，本研究定义变量Zi来描述两个样本之间第i个基因的转录是否发生变化，如果完全变化则Zi=1;完全不变化则Zi=0。

基于以上分析，本研究最终构建了一个概率模型PA来综合描述细胞中所有基因出现当前转录变化情形的概率:

其中，yi1，yi2为基因 i在两个样本中测得的转录值。λi1，λi2为基因 i在两个样本中的实际转录值。α1，β1，α2，β2，Zi为模型参数。P 为任一个基因在两个样本之间发生转录变化概率。

如果概率模型PA的模型参数得到准确求取，则通过Zi值就可以分析出第i个基因在不同样本间，其转录是否发生变化以及变化程度。Zi越大则变化程度越大，反之亦然。

在上述概率模型中，如果Zi已知，即第i个基因在两个样本间转录变化程度是已知的，则可以通过调整 α1，β1，α2，β2的取值，直接计算出 λi，λi1，λi2值并使得PA最大化，从而实现对两个样本中基因转录情形的透彻分析。但由于Zi的取值是未知的，无法一次对所有模型参数在PA最大化前提下进行求取，因此，采用统计学中预测概率最大化迭代算法来对 α1，β1，α2，β2进行 PA概率最大化条件下的求取，并最终确定 λi，λi1，λi2及其 Zi值，以确定每个基因是否在不同样本间发生转录变化及其变化程度。

这里采用的预测概率最大化算法分为反复迭代的两步。

第一步是概率预测，即假设 α1，β1，α2，β2已知的情况下求取Zi值。

首先对 λi，λi1，λi2进行估算，即在 yi1，yi2，α1，β1，α2，β2已知的情况下寻找 λi，λi1，λi2值使 PA最大。

若Zi=0:

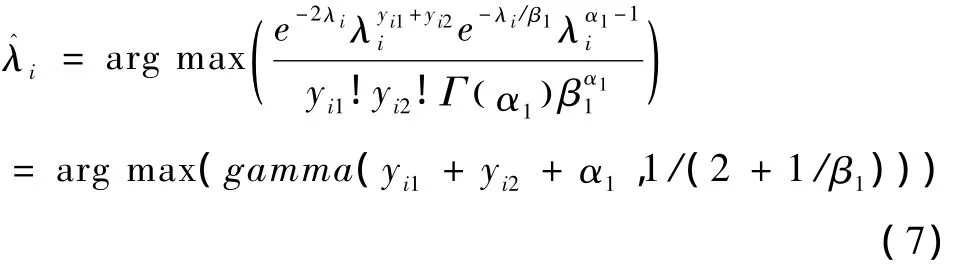
若Zi=1:

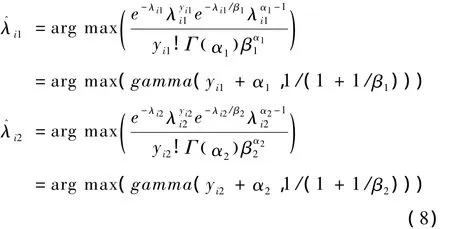
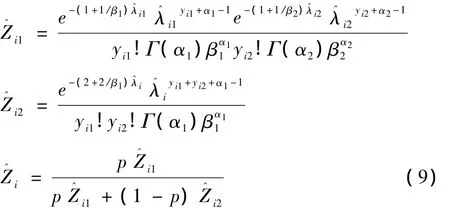
随后，Zi可估算为:第二步是概率最大化，即在计算出的情况下寻找最优的 α1，β1，α2，β2使 PA最大。通过对 PA表达式(6)的分析发现，这相当于通过寻找 α1，β1，α2，β2值使下两式最大

最后，对基因在两个样本之间发生转录变化的概率P值进行更新:

以上过程迭代进行，直至收敛。

1.3 粒子群优化

在应用预测概率最大化算法进行概率模型PA的模型参数求取过程中发现，针对第一步，即概率预测，其计算比较容易实现。但对于第二步，即概率最大化，如果进行精确的解析求解将很困难且计算量相当大。与之相对应，在复杂解空间内搜寻最优解恰好是智能寻优算法的优势［16］，因此，这里采用智能寻优算法中的粒子群算法，在概率最大化步骤中对模型参数直接进行数值解寻优求取。通过初步计算，发现模型参数 α1，β1和 α2，β2的解空间比较简单，因此采用基本粒子群算法进行 α1，β1和α2，β2的数值解求取。另外，在式(10)中，由于 α1，β1和 α2，β2不具有相关性，因此这里可对 α1，β1和α2，β2分别进行寻优。

具体粒子群算法设计如下:

算法初始化时，取h个粒子，其初始值均匀分布在二维解空间内。对于每个粒子，其解空间内当前位置矢量的评估函数采用式(10)。对于第k(k=1，…，h)个粒子，为了在解空间内搜索更优的位置矢量，其移动速度V′k采用下式进行更新

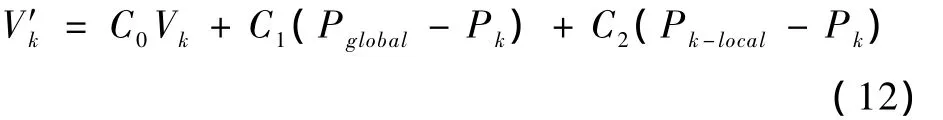
式中，Pk为第k个粒子在解空间内当前位置矢量。Pglobal为所有粒子中解空间内当前最优的位置矢量。Pk-local为第 k个粒子解空间内当前最优的位置矢量。Vk为第 k个粒子当前移动速度。C0，C1，C2为各部分权值以控制第k个粒子在解空间内的移动方向和速度。

最后，第k个粒子在解空间内的新位置矢量按下式计算:

以上过程重复进行，直至无法在解空间内找到更优的全局位置矢量。

2 实验测试结果和讨论

2.1 实验设计

为了对本研究所提出基因转录差异分析模型的有效性进行测试，这里将选取美国俄亥俄州立大学公开提供的两种MCF-7乳腺癌样本PolⅡ测量数据。一种样本是普通的MCF-7乳腺癌样本，另一种是具有抗药性的 MCF-7乳腺癌样本。该数据共分为四组，分别是加药前普通乳腺癌、加药后普通乳腺癌、加药前抗药乳腺癌和加药后抗药乳腺癌样本中利用DNA高通测序技术测得的25470个基因转录区内结合的PolⅡ蛋白数量。

按预计，在加药的情况下，普通乳腺癌样本内基因的转录变化将比抗药乳腺癌样本更剧烈，这构造出测试样本分析模型有效性的良好环境。

对这四组实验数据在进行PolⅡ总数归一化后的统计分析结果如表1所示。

表1 测试数据统计分析(单位:个)Tab.1 Statistical analysis of experiment data(Unit:Number )

由表1可以分析出，在4组测试数据归一化后，不同样本间的测试数据在均值一致的前提下方差变化有着明显的差异。其中，普通乳腺癌样本在加药后基因整体的转录差异明显降低，这可能是由于部分转录水平高的基因加药后转录水平得到抑制导致的;而抗药乳腺癌样本加药后基因的整体转录水平变化则不明显，这说明其对药物不敏感。这一现象是符合两种样本的自然特性的，因此，可证明实验测得数据是有意义的。

在获取所有基因整体的转录差异变化后，具体到每一个基因，如何评估其转录变化则将用本研究所提出分析模型进行分析。

2.2 基因转录差异分析

首先，如果某个基因所在DNA区域内组蛋白修饰或DNA甲基化等原因导致PolⅡ蛋白无法在其转录区内结合，则该基因转录将不遵循泊松分布。因此，为保证计算精度，在测试数据中将去除加药前后转录区内均没有结合PolⅡ蛋白的基因。这样处理后，在全部25 470个基因中，普通乳腺癌样本测试数据中将有24 020个基因参与后续分析，而抗药乳腺癌样本测试数据中有24 230个基因参与后续分析。

随后，将4组转录数据分成两个大组。每个大组含有一个乳腺癌样本加药前后的两组基因转录数据。然后分别采用本文所提出的基因转录差异分析模型对其进行个体基因转录差异分析。

在预测概率最大化算法的迭代参数优化过程中，在概率预测步骤中，由于针对n个个体基因构造的泊松模型参数 λi，λi1，λi2(i=1，…，n)的最优参数计算式(7)和式(8)也没有解析解，依据其所遵循的伽玛函数凸特性设计参数寻优算法如下:λi，λi1，λi2分别由1开始以1为步长进行增加并计算其对应的式(7)和式(8)中伽玛函数值，当函数值由小变大过程中首次出现下降时，在其对应的 λi，λi1，λi2值附近进行寻优，并找到 λi，λi1，λi2的最优值。在概率最大化步骤中，将采用粒子群优化算法。粒子群优化算法的参数设置为:粒子个数为100，C0=1，C1=2，C2=2。

对于普通乳腺癌和抗药乳腺癌两大组基因转录数据，预测概率最大化算法的参数寻优均在迭代4～5次后收敛，收敛后的 Zi(i=1，2，…，n)值将反映第i个基因转录变化的程度。其最终分析结果见表2和表3。

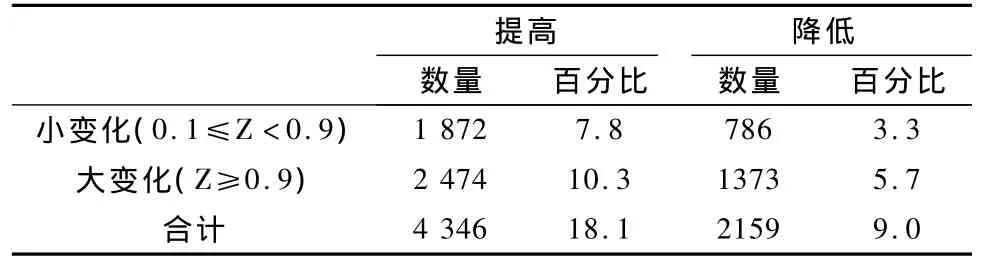
表2 普通乳腺癌分析结果Tab.2 Analytical results of normal breast cancer

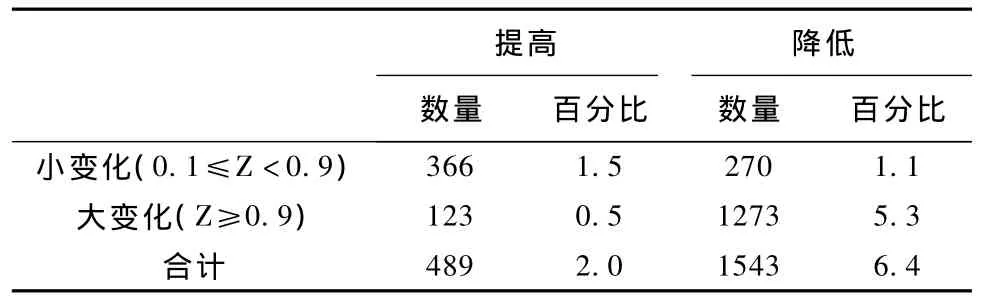
表3 抗药乳腺癌分析结果Tab.3 Analytical results of drug resist brea st cancer

结合表1和表2，普通乳腺癌样本加药后，尽管基因间整体转录差异有所降低，但就个体基因而言，在所考虑的24 020个基因中，仍有6505个基因的转录发生了明显变化，占27.1%。其中，转录提高的基因共有4 346(18.1%)个，提高幅度大的(Z≥0.9)有2 474(10.3%)个，提高幅度小的(0.1≤Z＜0.9)有1 872(7.8%)个。而转录降低的基因仅为转录提高基因数目的一半，有2 159(9.0%)个，其中降低大的为1 373(5.7%)，降低小的为786(3.3%)。可见加药后，普通乳腺癌样本的反应还是较剧烈的，更多的反应是基因的转录水平发生了提高。

结合表1和表3，抗药乳腺癌样本加药后，尽管基因间整体转录差异变化不大，但就个体基因而言，仍有6 505(8.4%)个基因的转录发生了明显变化。其中，转录提高的基因较少，仅有489(2.0%)个，提高幅度大的有123(0.5%)个，提高幅度小的有366(1.5%)个。而转录降低的基因有1 543(6.4%)个，其中降低大的为1 273(5.3%)，降低小的为270(1.1%)。可见加药后，抗药乳腺癌样本的反应相比普通乳腺癌样本明显减弱。而这种减弱主要体现在加药后基因的转录反而受到了抑制，这从基因转录降低的数目明显多于基因转录提高数目中可以看出。

从以上分析可以看出，加药对普通乳腺癌样本和抗药乳腺癌样本的影响有着明显的不同，相比较而言，普通乳腺癌样本比抗药乳腺癌样本对加药的反应要强烈得多。而这种差异与实验设计的预期结果是相吻合的。这充分反映出本研究所提出基因转录差异分析模型的有效性。

3 结论

利用可直接反映基因转录水平的基因转录区内所结合PolⅡ 蛋白的个数，提出一个分析模型，分析每一个基因在两个相关样本间转录水平的变化程度，通过实际数据测试证明了该模型的有效性。

由于不同样本不同实验下所测得PolⅡ 蛋白整体个数差异较大，因此，即使通过归一化进行了校正，仍然会对本研究所提出模型的分析精度造成影响。目前，随着DNA测序技术的发展，一次实验所测得的数据越来越大。据估计，2009年年底该数字将达到1000亿个碱基和30亿条读数。随着测试数据量的提高，不同实验下所测得PolⅡ 蛋白整体个数差异对本模型分析精度的影响将会越来越小。

另外，为了使分析结果有明显的生物含义，所提出的模型是基于这样一个前提设计的:即如果两个样本间基因转录水平未发生明显变化，则其转录分布特性是基本不变的。这样处理的好处是如果找到两个样本间转录分布特性发生明显变化的基因，该基因就很可能与两个样本的自然差异有关(如加药反应，癌病变等)。因此，只要遵从这一前提，本研究所提出模型即可用于对两个样本间基因转录水平的差异进行分析，也可以用于多样本分析。具体方法可以以一个样本为基准，其它样本对其分别利用本研究所提出模型进行计算，并将所有计算结果集中在一起进行综合分析即可。

此外，由于PolⅡ 蛋白的个数只能反映基因转录水平，不能直接反映更有生物意义的基因表达水平，因此本模型还有待进一步发展，以最终用于基因表达差异分析。目前，最新发展的生物技术已使RNA高通测序成为可能。相比于DNA高通测序仅在DNA层次反映样本组织的基因转录模式，RNA高通测序则可直接测量样本组织中所有基因是否表达以及表达的程度。这就为直接对基因表达差异分析提供了可能。针对这一新技术，通过将分析对象由基因转录区内所结合 PolⅡ 蛋白个数替换为反映该基因表达水平的RNA高通测序序列读数，本模型即可用于分析两个相关样本间基因表达差异分析，但具体实现方式还有待针对RNA高通测序技术进行进一步研究。

［1］张晓龙，杨艳霞.机器学习在生物信息学中的应用［J］.武汉科技大学学报，2005，28(2):201-204

［2］Kerr MK，Martin M，Churchill GA.Analysis of variance for gene expression microarray data［J］.Journal of Computational Biology，2000，7:819-837.

［3］Wolfinger RD，Gibson G，Wolfinger ED.et al.Assessing Gene Significance from cDNA Microarray Expression Data via Mixed Models［J］.Journal of Computational Biology，2001，8:625-637.

［4］Dudoit S，Yang YH，Callow MJ，et al.Statistical methods for identifying differentially expressed genes in replicated cDNA microarray experiments［J］.Statistica Sinica，2002，12:111-139.

［5］Schmidt D，Wilson MD，Spyrou C，et al.ChIP-seq:Using high-throughput sequencing to discover protein-DNA interactions［J］.Methods，2009，48(3):240-247.

［6］Johnson DS，Mortazavi A，Myers RM，et al.Genome-wide mapping of in vivo protein-DNA interactions［J］.Science，2007，316:1497-1499.

［7］Ansorge WJ.Next-generation DNA sequencing techniques［J］.N Biotechnol，2009，25(4):195-203.

［8］Fullwood MJ，Wei CL，Liu ETB，et al.Next-generation DNA sequencing of paired-end tags(PET)for transcriptome and genome analyses［J］.Genome Res，2009，19(4):521-32.

［9］Cole T，Lior P，Steven LS.TopHat:discovering splice junctions with RNA-Seq［J］.Bioinformatics，2009，25(9):1105-1111.

［10］Daniel RZ，Ewan B.Velvet:Algorithms for de novo short read assembly using de Bruijn graphs［J］.Genome Res，2008，18(5):821-829.

［11］David JS，William GR.Transcriptome sequencing of malignant pleural mesothelioma tumors［J］.PNAS，2008，105(9):3521-3526.

［12］特纳PC著.分子生物学［M］.(第2版).北京:科学出版社，2001.

［13］Raja J，Suresh C.Genome-wide identification of in vivo protein-DNA binding sites from ChIP-Seq data［J］.Nucleic Acids Research，2008，36(16):5221-5231.

［14］Newton MA，KendziorskiCM，RichmondCS，etal.On differential variability of expression ratios:Improving statistical inference about gene expression changes from microarray data［J］.Journal of Computational Biology，2001，8:37-52.

［15］Kendziorski C，Newton M，Lan H，et al.On parametric empirical bayes methods for comparing multiple groups using replicated gene expression profiles［J］.Stat Med，2003，22(24):3899-3914.

［16］Parsopoulos KE，Vrahatis MN.Recent approaches to global optimization problems through Particle Swarm Optimization［J］.Natural Computing，2002，1:235-306.

A Model for Analyzing Gene Transcription Difference Using Particle Swarm Optimization

FENG Wei-Xing*WANG Ke-Jun
(Pattern Recognition and Intelligent System Institute of Harbin Engineering University，Harbin，Heilongjiang 150001，China)

Q332

A

0258-8021(2010)02-0229-06

10.3969/j.issn.0258-8021.2010.02.012

2009-07-10，

2009-11-04

国家高技术研究发展(863)计划(2008AA01Z148)

*通讯作者。 E-mail:fengweixing@hrbeu.edu.cn