非下采样Contourlet变换医学图像融合性能研究

胡俊峰唐鹤云钱建生

1(徐州医学院医学影像学院，徐州 221006)2(中国矿业大学信息与电气工程学院，徐州 221008)

非下采样Contourlet变换医学图像融合性能研究

胡俊峰1，2*唐鹤云1钱建生2

1(徐州医学院医学影像学院，徐州 221006)2(中国矿业大学信息与电气工程学院，徐州 221008)

通过对非下采样Contourlet变换(NSCT)滤波器组合及图像融合规则性能的研究，比较了不同条件得到的融合结果，全面分析了各种融合规则对融合性能的影响。提出低通子带区域能量取大，高频子带方差加权取大和绝对值取大相结合的融合算法。相比基于传统规则的NSCT算法，所提出算法的融合质量及各项指标都有明显提高。实验结果表明，选取合适的滤波器组合和融合规则，即使分解层数较少，方向数不大，也能够获得理想的融合效果，同时还可有效减少融合算法的复杂度。

图像融合;非下采样Contourlet变换;滤波器组合;融合规则;效果评价

Abstract:Effects of the nonsubsampled contourlet transform(NSCT)were analysed and the fusion results using different filters and fusion rules were compared.An efficient fusion method was proposed fusing the lowfrequency coefficients based on region energy rule and the directional high-frequency coefficients based on region variance or weighted region variance and coefficient absolute value rules.Experimental results showed the improved fusion quality compared with the traditional NSCT algorithm.Appropriate filter combination and fusion rules could bring a satisfying fusion result even with less decomposing levels and directional banks.Besides，the proposed method could reduce the fusion algorithms complexity.

Key words:image fusion;nonsubsampled contourlettransform;filters combination;fusion rule;quality evaluation

引言

多种成像模式提供的信息常常具有互补性，图像融合是指将由不同传感器或同一传感器在不同时刻所获得的多幅图像经过一定的处理、综合，以获取对同一场景的更为精确、全面的图像描述。它广泛应用于地球遥感、资源探测、军事侦察、机器视觉和医学图像后处理技术等诸多领域［1-2］。

近年来，小波变换由于其多分辨率、时频局部等特性，被广泛应用于图像处理领域，并且成为图像融合领域的重要算法［3-5］。然而二维可分小波不能有效地捕捉轮廓信息，是一种“非稀疏”图像表示法。为了解决小波这一局限性，新的理论不断发展。2002年Do M N和 Vetterli M提出了一种“真正”的二维图像表示算法即 Contourlet变换［6-9］。相对于小波变换，Contourlet变换除了具有多尺度、时频局部特性外，还具有方向特性。但是，在对图像进行Contourlet变换的过程中，需要对图像进行下采样操作，从而使得Contourlet变换不具备平移不变性，这在奇异性方面会产生伪吉布斯(pseudo-Gibbs)现象，导致图像失真。为此 Cunha等［10］又提出一种具有平移不变性的Contourlet变换，即非下采样 Contourlet变换(nonsubsampledcontourlet transform，NSCT)。该变换比 Contourlet变换具有更灵活的多分辨、多方向的图像表示能力，且以冗余度换取了平移不变性［10-12］。由于该变换具有平移不变性，而且具有足够的冗余信息，因此可以有效提取待融合图像中的方向信息，使得融合后的图像更好地满足人眼的视觉要求。

本研究从NSCT变换本身出发，通过调整滤波器组合及低通子带和高通子带融合规则，深入讨论了NSCT变换各种滤波器组合和融合规则的特性，分析了各种融合规则对融合结果的影响。在此基础上，考虑到医学图像的频谱随着分解层数的增加，在高频处最外层方向性不强，信息不丰富，提出低通子带区域能量取大、高频子带方差加权取大和绝对值取大相结合的融合方法，比基于传统规则的NSCT算法的融合质量及各项指标都有明显提高，验证了理论分析与实验结论的有效性。实验证明，选取合适的滤波器组合和融合规则，即使分解层数较少，方向数不大，也能够获得理想的融合效果。这大大减少了融合算法的复杂度。

1 基于非下采样Contourlet变换的图像融合机理

非下采样Contourlet变换是将多尺度分析和方向分析分开进行，首先采用非下采样塔式滤波器组(nonsubsampled pyramid filter bank，NSPFB)对图像进行多尺度分解，然后再采用非下采样方向滤波器组(nonsubsampled directional filter bank，NSDFB)对得到的各带通子带图像进行方向分解，从而得到不同尺度、方向子带图像(系数)。

图1(a)为非下采样 Contourlet变换的分解框图。首先，用非下采样金字塔变换将输入图像分解为低通子带和高通子带，以实现图像的多分辨率分解;然后利用非下采样方向滤波器组，将高通子带分解为多个方向子带，方向子带的数目可以是2的任意次幂(图1(b))。这一过程可以在NSPFB输出的低频子带重复迭代进行，以实现图像的多方向分解;最后对每一层的低通子带重复上述操作，即可得到输入图像的多层非下采样 Contourlet变换。

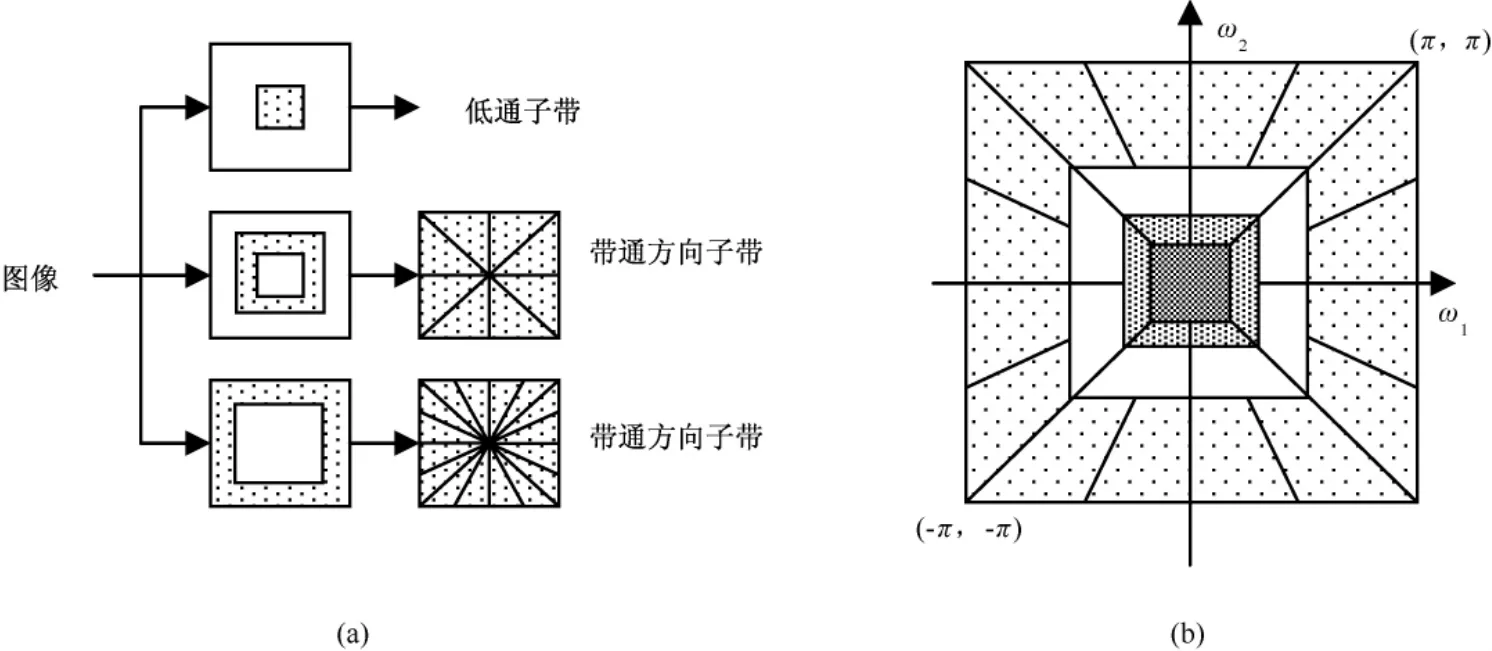
图1 非下采样 Contourlet变换。(a)块分解图;(b)NSCT频率划分图Fig.1 Nonsubsampled contourlet transform.(a)nonsubsampled directional filter bank decomposition structure;(b)NSCT frequency domains

2 基于非下采样Contourlet的融合算法

像素级的融合简单、直接，能够保留尽可能多的信息，具有较高的精确度。本研究主要考虑的是像素级的图像融合。NSCT分解后的低频信息和高频信息具有不同的物理意义，低频信息保留了原始图像的概貌信息，高频信息中绝对值较大的系数对应着一些突变，如图像的边缘、纹理等重要特征信息。因此需要对图像的高频细节信息和低频近似信息加以区分，采用不同的融合算子和融合规则。不同的融合规则具有各自的优缺点，如果从融合规则组合与选取的过程中，探寻出融合规则的选取规律，就可以指导简便快捷的融合算法的提出。

图像融合过程中，融合规则的选择对于融合的质量非常重要。常用的低频子带融合准则包括:平均 (average，AVE)的准则、选取区域方差 (region variance，RVA)最大的准则。常用的高频子带融合准则包括:选取系数绝对值 (coefficient absolute value，CAV)最大的准则、选取区域能量 (region energy，REN)最大的准则［11-13］。

根据多传感器图像非下采样 contourlet变换的特点，提出低频能量取大、高频中间分层方差取大以及方差加权取大、最外层分解绝对值取大的NSCT融合方法，以验证融合规则选取的重要性。下面以两幅图像的融合为例，来说明基于非下采样contourlet变换的图像融合算法实现。具体实现步骤如下:

步骤1:对已配准的两幅图像分别标记为图像A和图像B。

步骤2:选取合适的滤波器组合。

步骤3:对图像A和B分别作基于NSCT的J层分解，首先NSPFB将图像分解得到各个尺度上的低频子带和带通子带{DA(m，n)，0≤j≤J-1}，{DB(m，n)，0≤j≤J-1}，然后 NSDFB 对带通子带作方向分解，将其分解为多个高频方向子带表示在尺度2-l上的高频方向子带数目表示在图像 A在尺度2-l上的第j个方向子带。并分别得到其变换系数，其中为图像A低频子带系数为图像 A 各个带通方向子带系数。对低频子带系数和各带通方向子带系数分别采用不同融合规则，得到融合图像F的NSCT的系数。

步骤4:进行非下采样Contourlet逆变换从而得到融合图像F。

1)低频子带融合规则

低频子带保留了原始图像的概貌信息，对于低频部分处理的主要目的是尽可能地保留这些概貌特征。本研究选取区域能量 (Region energy，REN)最大的准则求取低频子带系数。区域能量定义为

其低频子带的融合系数为

式中，X=A、B，Ω(m，n)表示以(m，n)为中心的小邻域(选取3×3)分别表示源图像A，B和融合图像F低频子带系数。

2)高频子带融合规则

高频子带中绝对值较大的系数对应着一些突变，如图像的边缘、纹理等重要特征信息。对于高频部分处理的主要目的是尽可能地增加融合图像的细节信息。本研究提出采用中间各分层方差取大以及方差加权取大、最外层分解系数绝对值取大的NSCT融合方法。

区域方差 (region variance，RVA)最大准则的区域方差定义为

区域方差加权 (weighted region variance，WRVA)最大准则定义为

最外层分解选取系数绝对值 (coefficient absolute value，CAV)最大的准则，即

3 图像融合质量评价

图像质量的评价方法原则上可以分为主观评价方法和客观评价方法两类。图像质量客观评价方法是当前的研究重点［14-15］，其共同点是用物理方法对图像的物理特性进行度量，将度量值与规定标准进行比较，利用数字模型来度量图像质量;具有计算速度快、稳定、不会因人而异、因时而异、易于被量化、易于比较研究等特点。

常用的客观评价标准有图像均值、标准差、信息熵、平均梯度、空间分辨率，近年来有人提出了边缘信息评价因子［16］等。图像均值是像素的灰度平均值，对人眼反映为平均亮度。标准差反映了图像灰度相对于灰度平均值的离散情况。标准差大，则图像灰度级分布分散，图像的反差大，可以看出更多的信息。标准差小，则图像反差小，对比度不大，色调单一、均匀，看不出太多的信息。信息熵是衡量图像信息丰富程度的一个重要指标，熵值的大小表示图像所包含的平均信息量的多少。如果融合图像的熵增大，表示融合图像的信息量增加，融合图像所包含的信息就越丰富，融合质量越好。平均梯度具有敏感地反映图像中微小细节的能力，同时还可以反映出图像中的纹理变换特征，可以用来评价图像的清晰度。空间频率反映了一幅图像空间的总体活跃程度。

边缘信息评价因子是一种新的基于边缘信息的性能评价因子，反映了源图像与融合图像边缘信息的传递量，大小越接近1说明边缘传递越好，融合效果也就越好。其公式为

式中，QABF表示融合图像 F相对于源图像 A、B的整体边缘保留量，QAF和QBF分别表示融合图像F相对于源图像A、B的边缘保留量，gA和 gB源图像A，B的边缘强度。

4 实验研究

首先研究非下采样 Contourlet变换滤波器的组合特性，找到性能优秀的滤波器的组合;在此基础上讨论融合规则对融合性能的影响，从而提出合适的融合算法;然后进行融合规则验证以确定所提出的融合规则的有效性与正确性。待融合图像选择已配准后的CT、MRI灰度图像，验证图像选用Lena标准图像，大小为256像素×256像素，PNG格式(图2(a)(b)、图5(a))。实验平台为Mobile AMD SempronTMProcessor 3200+1.6 GHz，521 MB 内存，Mtlab7.01。

4.1 滤波器组合的选择

非下采样 Contourlet变换首先用非下采样金字塔滤波器(NSPFB)将输入图像分解为低通子带和高通子带，以实现图像的多分辨率分解;然后利用非下采样方向滤波器组(NSDFB)将高通子带分解为多个方向子带。常用的NSPFB二维滤波器有9-7、maxflat、pyr、pyrexc 四种，二维方向滤波器(NSDFB)有 harr、db、coif、qmf、test、vk、ko、kos、lax、sk、cd、pkva、oqf_362、dvmlp、sinc、dmaxflat等十七种。虽然四种不同的NSPFB都能满足多尺度分解，同时十七种方向滤波器也能完成方向分解，但是由于各种滤波器互有不同，滤波器的选择与组合方法直接影响着融合的性能。

选择上述四种不同的非下采样金字塔滤波器与十七种方向滤波器分别组合进行融合实验。具体方法是任选一种NSPFB和十七种NSDFB组成一组，共四组。融合规则统一选择常用的低频子带系数平均法，高频方向子带绝对值取大法。为了进一步说明滤波器组合对于各层分解的影响，将分别获得不同滤波器在二层方向分解后的图像，以观察和分析二层方向分解图像的不同。选用客观评价标准:均值、标准差、信息熵、平均梯度、空间分辨率分别对每组进行融合结果评价。

4.2 融合规则的选取

文献［11-13］已经对NSCT变换与小波变换和Contourlet变换进行了详细对比，证实了 NSCT变换优于后两种融合变换方法，由于篇幅限制，文中不再述及。主要对NSCT变换的各种融合规则进行对比分析和选优。实验方法选取常用的平均法、绝对值取大、能量取大［12］、方差取大［13］规则进行组合，分解层数［0，1，2］，滤波器组合选取 4.1中表现优秀的9-7和lax滤波器组合参与实验，进行不同融合规则的选取对融合性能影响的实验研究，并与文献［12-13］中提出的基于能量取大与方差取大方法进行比对，以提出新的有效融合规则。为了说明融合规则对于各层融合的影响，实验首先对两幅图像的方向子带二层分解图像分别进行绝对值取大与方差取大融合，以观察二层方向分解图像融合结果的不同。融合评价采用主观视觉分析与客观标准共同进行，客观标准选取标准差、信息熵、平均梯度分别对每组进行融合结果评价，为了对融合结果边缘信息进行有效检测，引入了边缘评价因子。

4.3 融合规则的验证

为了验证上述实验与理论分析的正确性和普遍有效性，选取Lena标准图像，采用左右分别聚焦的方式获得多聚焦源图像(图5(b)(c))，选取4.2实验中的各种规则组合模式进行融合验证。

5 实验结果和分析

表1为4.1滤波器组合的图像融合性能指标。由于篇幅的限制，只给出了 lax、db3滤波器与NSPFB滤波器组合的融合结果，可以看出以lax滤波器组合图像融合效果各项指标分别优于db3滤波器组合。而在各种组合中NSPFB滤波器以9-7为首选。造成各种滤波器组合的融合结果不同的原因在于各种滤波器性能不一样，图2给出了不同滤波器在二层方向分解后分别获得的图像，实验结果显示9-7、db3组合二层方向分解图像含有的信息明显少于9-7、lax组合二层分解图像，标准差、信息熵、平均梯度、空间分辨率都明显小，说明9-7、db3组合融合图像对比度小、信息少、细节反映度不高;同时说明9-7、lax滤波器组合分解的信息多，方向性更强，具有较好的高频特性。为了更好的发挥NSCT变换高频多方向性的优势，就要选择高频信息较多的滤波器组合进行图像融合研究。

表1 二组滤波器组合图像融合性能指标比较Tab.1 Comparison the image fusion of two group filters

图2 不同滤波器组合图像第二层方向分解结果。(a)CT图像;(b)MRI图像;(c)9-7＆db3组合分解;(d)9-7＆lax组合分解Fig.2 Second directional decomposition image of different group filters.(a)CT image;(b)MRI image;(c)9-7＆db3 filters directional decomposition image;(d)9-7＆lax filters directional decomposition image

图3给出了4.2不同融合规则的方向子带二层分解和融合效果。可以看出绝对值取大在该层的融合效能并没有显现，表现为融合结果没有第二幅图像的信息(图3(c));而方差取大的融合效果明显(图3(d))。说明选取不同融合规则对融合结果影响很大。表2给出了各种算法融合图像的客观评价性能指标，图4为实验结果融合图像。实验结果证明基于能量取大规则对亮度和灰度影响较大，表现为标准差和信息熵大，而方差取大规则对图像清晰度有较强影响，表现为平均梯度大。说明区域能量擅长低频概貌的获取，而方差对图像高频细节捕捉能力较强;二者结合显著提高了融合质量，即低频REN、高频 RVA规则具有明显优势(图4(d))。但是如果低频采用方差取大准则［11］，尽管评价客观数据较好，由于方差取大的本身特性，导致融合图像对比度太强，影响了融合图像的进一步应用，尤其是医学融合图像应用于临床时，将明显增加错误诊断，导致误诊率的提高(图4(b)(c))。方差取大的另一个缺点是运行时间较长;研究发现低频平均法(AVE)融合图像太暗，灰度及边缘保持较差(图4(a))，绝对值取大(CAV)仍有一定优势(表2)。

为了充分利用能量取大低频概貌和方差取大细节优势，考虑到医学图像的频谱随着分解层数的增加，在高频处最外层方向性不强、信息不丰富，方差取大可以与绝对值取大结合运用，从而提出了低频能量取大、中间分层方差取大、最外层绝对值取大准则，即低频 REN，高频 RVA+CAV(即 R+C)(图4(e))。在此基础上探讨低频能量取大、中间分层方差加权取大、最外层绝对值取大准则，即低频 REN，高频 WRVA+CAV(即 WR+C)(图4(f))。于相比基于传统规则的NSCT算法的各项指标有明显提高，融合结果显示标准差、信息熵、平均梯度、边缘信息值大，说明融合图像对比度大、细节反映度高、灰度信息丰富、边缘保持好;相比单纯的低频能量取大高频方差取大，大大节省了运行时间;而WR+C较R+C清晰度及灰度信息以及边缘保持都有改进。实验结果证明了方法的有效性及融合规则选取的重要性。结果表明NSCT变换的不同，融合规则性能亦不同，高低频及各方向子带均可以单独选择融合规则，正确的选择融合规则组合可以获得理想的融合效果。

图3 方向子带二层分解和融合结果。(a)CT图像二层分解;(b)MRI图像二层分解;(c)绝对值取大融合;(d)方差取大融合Fig.3 Second decomposition of directional bank and fusion image.(a)CT image of second directional decomposition;(b)MRI image of second directionaldecomposition;(c)CAV rulefusion image;(d)RVA rule fusion image

表2 不同融合规则对图像融合性能指标影响比较Tab.2 Comparison the image fusion of different fusion rules

图4 不同规则图像融合效果。(a)AVE＆CAV融合图像;(b)RVA＆REN融合图像;(c)RVA＆RVA融合图像;(d)REN＆RVA融合图像;(e)REN＆R+C融合图像;(f)REN＆WR+C融合图像Fig.4 Image fusion results of different fusion rules.(a)AVE＆CAV rule fusion image;(b)RVA＆REN rule fusion image;(c)RVA＆RVA rule fusion image;(d)REN＆RVA rule fusion image;(e)REN＆R+C rule fusion image;(f)REN＆WR+C rule fusion image

表3为4.3算法规则验证实验的融合性能指标对比情况，图5给出了实验结果。实验结果同样表明低频RVA、高频RVA规则(图5(f))融合指标明显优于低频RVA、高频规则 REN(图5(e))，说明高频选用 RVA规则优于高频 REN规则，基于低频REN、高频RVA规则融合质量及各项指标优于文献［12-13］提出算法。而本研究提出的低频能量取大、中间分层方差加权取大、最外层绝对值取大准则，即低频 REN，高频 WRVA+CAV(即 WR+C)(图5(h))，相比于基于传统规则的NSCT算法的各项指标有明显提高，相比单纯的低频能量取大高频方差取大，大大节省了运行时间，灰度信息以及边缘保持都有改进。实验结果再次证明了本方法的有效性及融合规则选取的重要性。为了能够清晰的表明实验结果，图6是把图5中各图的眼部细节分别放大所得图像，直观显示了融合结果，从而进一步验证了本算法的有效性。

表3 不同融合规则对图像融合性能影响比较Tab.3 Comparison the image fusion of different fusion rules

图5 不同规则图像融合效果。(a)Lena图像;(b)左聚焦图像;(c)右聚焦图像;(d)AVE＆CAV规则融合图像;(e)RVA＆REN融合图像;(f)RVA＆RVA融合图像;(g)REN＆RVA规则融合图像;(h)REN＆WR+C规则融合图像Fig.5 Image fusion results of different fusion rules.(a)Lena image;(b)right focus image;(c)left focus image;(d)AVE＆CAV rule fusion image;(e)RVA＆REN rule fusion image;(f)RVA＆RVA rule fusion image;(g)REN＆RVA rule fusion image;(h)REN＆WR+C rule fusion image

图6 不同规则图像融合比较。(a)Lena图像;(b)左聚焦图像;(c)右聚焦图像;(d)AVE＆CAV规则融合图像;(e)RVA＆REN融合图像;(f)RVA＆RVA融合图像;(g)REN＆RVA规则融合图像;(h)REN＆WR+C规则融合图像Fig.6 Comparison the image fusion results of different fusion rules.(a)Lena image;(b)right focus image;(c)left focus image;(d)AVE＆CAV rule fusion image;(e)RVA＆REN rule fusion image;(f)RVA＆RVA rule fusion image;(g)REN＆RVA rule fusion image;(h)REN＆WR+C rule fusion image

6结论

本研究详细分析了非下采样Contourlet变换滤波器组合以及融合规则选取对图像融合性能的影响。研究表明NSCT变换中不同的滤波器组合分解效果不同，不同融合规则性能不同，高低频及各方向子带均可以单独选择融合规则，正确的选择融合规则组合可以获得理想的融合效果。提出了低通子带区域能量取大，高频子带方差加权取大和绝对值取大相结合的融合算法，比基于传统规则的NSCT算法的融合质量及各项指标都有明显提高，有效地验证了方法的有效性。理论分析和实验结果证明:选取合适的滤波器组合，即使分解层数较少，方向数不大，配以合适的融合规则，就能够获得理想的融合效果，这大大减少了融合算法的复杂度。实验结果对NSCT的深入研究具有较大的指导意义。

［1］Matsopouios GK，Marshall S，Brunt J.Multi-resolution morphological fusion of MR and CT images of the human brain［J］.IEEE Transactions on Image and Signal Processing，1994，141(3):137-142.

［2］Wang A，Sun Haijing，Guan Yueyang.The application of wavelet transform to multi-modality medical image fusion［A］.In: Proceedings of IEEE international Conference on Networking，Sensing and Control［C］.Chicago:IEEE，2006.270-274.

［3］张泾周，李婷，吴疆.医学图像的小波变换融合算法研究［J］.中国生物医学工程学报，2008，27(4):521-525.

［4］Jian Muwei，Dong Junyu，Zhang Yang.Image fusion based on wavelet transform ［A］.In:Proceedings of the 8th ACIS International Conference on Software Engineering，Artificial Intelligence，Networking，and Parallel/Distributed Computing［C］.Chicago:IEEE，2007.713-718.

［5］胡俊峰，唐彩银，巩萍.基于小波变换的 CT/SPECT图像融合最佳层数选取［J］.中国医疗设备，2009，24(3):10-12.

［6］Do MN，Vetterli M.Contourlet:A directional multiresolution image representation［A］.In:Processings of IEEE International Conference on image Processing［C］.Rochester:IEEE，2002.357-360.

［7］Do MN，Vetterli M.The contourlet transform:an efficient directionalmultiresolution image representation［J］.IEEE Transactions on Image Processing，2005，14(12):2091-2106.

［8］才溪，赵巍.Contourlet变换低通滤波器对图像融合算法影响的讨论［J］.自动化学报，2009，35(3):258-266.

［9］Do MN，Vetterli M.Pyramidal directional filter banks and curvelets ［A］.In:Proceedings of IEEE International Conference on Image Processing［C］.Thessaloniki:IEEE，2001.3:158-161.

［10］Cunha AL，ZhouJiangping，Do MN.Thenonsubsampled contourlet transform:theory，design，and applications ［J］.IEEE Transactions on Image Processing，2006，15(10):3089-3101.

［11］郭雷，刘坤.基于非下采样 Contourlet变换的自适应图像融合算法［J］.西北工业大学学报，2009，27(2):255-259.

［12］张强，郭宝龙.基于非采样 Contourlet变换多传感器图像融合算法［J］.自动化学报，2008，34(2):135-141.

［13］贾建，焦李成，孙强.基于非下采样 Contourlet变换的多传感器图像融合［J］.电子学报，2007，35(10):1934-1938.

［14］Zheng Sheng，Shi Wenzhong，Liu Jian，et al.Multisource image fusion method using support value transform［J］.IEEE Transactions on Image Processing，2007，16(7):1831-1839.

［15］Wang Zhijun，Djemel Z，Costas A，et al.A comparative analysis of image fusion methods［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，9(18):2137-2143.

［16］Xydeas CS，Petrovic V.Objcetive image fusion performance measure［J］.Electronics Letters，2000，36(4):305-309.

Research of Medical Image Fusion Algorithms Based on Nonsubsampled Contourlet

HU Jun-Feng1，2*TANG He-Yun1QIAN Jian-Sheng2
1(School of Medical Imageology，Xuzhou Medical College，Xuzhou 221006，China)2(School of Information and Electric Engineering，China University of Mining and Technology，Xuzhou 221008，China)

R318.04

A

0258-8021(2010)04-0509-08

10.3969/j.issn.0258-8021.2010.04.006

2009-12-30，

2010-04-15

江苏省高校科技成果转化项目(JHZD09-22);徐州市科技计划项目 (XM09B070)

*通讯作者。 E-mail:hjf098@yahoo.com.cn