基于电力信号特征的FIR滤波器的优化

陈邦琼

(健雄职业技术学院计算机工程系 江苏太仓 215411)

基于电力信号特征的FIR滤波器的优化

陈邦琼

(健雄职业技术学院计算机工程系 江苏太仓 215411)

对FIR数字滤波器频响的振荡特性及其产生的原因进行了深入分析，并结合其在电力系统中的应用，给出了在保证频响满足要求的前提下，可显著降低滤波器阶数的优化方法——旁瓣重合法。通过在Matlab/Simulink平台上仿真，证明了这种方法的有效性。

FIR;数字滤波器;窗函数;旁瓣重合法

滤波器技术是电子信息领域中非常基本而又十分重要的信号处理手段。而随着软、硬件技术水平的快速提升，数字滤波器更是得到了广泛应用。数字滤波器根据冲击响应函数的时域特性，可以分为FIR(有限长冲击响应滤波器)和IIR(无限长冲击响应滤波器)。FIR滤波器与IIR滤波器相比，具有严格的线性相位、幅度特性可任意、运算效率高等优点。基于此，FIR数字滤波器在很多情况下得到应用。电力信号的显著特点就是其主频为工频，其他信号主要是50 Hz基频的高次谐波，其中奇次谐次波的比例更高一些。在对电力信号进行数据采集时，针对其信号特点，对数字滤波器进行优化，可在保证数据精度的前提下，降低滤波器规模。

1 FIR数字滤波器结构加窗特点和频响特性

FIR滤波器的传递函数可表示为:

1.1 FIR数字滤波器结构加窗特点

用软件和硬件方法均可以实现式(1)所示的传递函数。但无论是用软件还是硬件方法，n的取值范围N都只能是有限值。因此FIR数字滤波器设计的主要原则之一就是在保证频响满足要求的前提下，尽可能降低滤波器的阶数。

由于N取有限值，式(1)可写为:

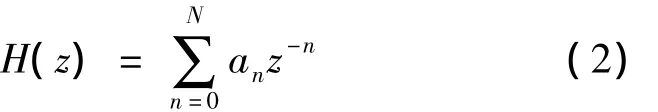
显而易见，式(1)中大于N的序列被舍弃掉了，这个过程谓之截短［2］，从信号分析的角度，相当于在式(1)的无限长序列上乘了一个宽度为N的窗函数:

由于FIR数字滤波器在实现中，必须对传递函数的求和序列进行截短，所以FIR数字滤波器的结构中必定包括一个合适的窗函数。

1.2 窗函数频响的振荡现象及原理分析

式(3)所示的窗函数未对求和序列进行修正，故称其为矩形窗函数，由于N取有限值，从而产生频谱搬移，引起矩形窗函数的频响存在混叠现象，于是又出现了各种旨在消除混叠现象、改善频响的各种窗函数，如汉明窗、凯泽窗、巴特利特窗、海宁窗、布拉克曼窗等;再者，窗函数的频响自身具有振荡特性，势必引起FIR数字滤波器的频响也具有振荡特性，即所谓的旁瓣现象。下面对窗函数的振荡特性进行分析。

1.2.1 矩形窗函数矩形窗函数如式(3)所示，其频响为:

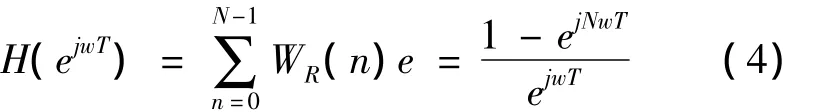
其中T为采样周期。显而易见式(4)在(0，π/ T)范围内是w的振荡函数，且w的振荡周期为:

假定取N=∞，则上式频响周期为无穷大，也就是说其频响不具有振荡特性，对应的FIR数字滤波器将表现出与理想滤波器完全相同的频响特性。当然，这在实际中是不可能实现的。

1.2.2 汉明窗

窗函数如式(6)所示:

其频响:

其中

则汉明窗函数的频响如式(8):

式(8)中的三项结构相似，所以汉明窗函数的频响也具有振荡特性，且周期也是，所不同的是后两项的初相位不为零，分别是

从以上对矩形窗函数和汉明窗函数的分析可见，窗函数频响具有振荡特性，其周期，由采样频率fs和窗函数宽度N决定。通过分析，其他常用的窗函数的频响也具有振荡特性，且周期宽度也满足式(5)，这里不再展开。窗函数的振荡特性是FIR滤波器出现振荡现象的主要原因。因此，FIR滤波器频响的旁瓣宽度与窗函数的振荡周期基本一致，如式(5)所示。

2 基于电力信号特征的FIR数字滤波器的优化

2.1 旁瓣重合法

电力信号的特点是谐波丰富，尤其是奇次谐波的分量所占比重大;因此，在对电力信号提取基波信息时的滤波，主要任务是滤除谐波，特别是奇次谐波。基于此，本文提出一种FIR数字滤波器优化方法——旁瓣重合法，充分利用FIR数字滤波器频响的旁瓣现象，尽可能让旁瓣的低谷频率点与各次谐波的频率一致，这样就可以对相应频率的谐波获得较高的衰减。具体方法是:首先根据需要重点抑制的谐波频率最小间距，确定FIR数字滤波器频响旁瓣宽度(如在电力系统中，一般主要考虑对奇次谐波的抑制:3、5、7……次谐波等，因此旁瓣宽度应为100 Hz)，再根据系统选定的对传感器信号的采样频率fs，依据式(5)，即可确定窗函数宽度N。由采样频率fs和窗函数宽度N，在MATLAB/smulink上就可以方便地确定FIR滤波器的各项系数。

2.2 仿真实例

设计一牵引电力系统用带通滤波器:要求30 Hz以下衰减在20 dB以上，二次以上奇次谐波的衰减在40 dB以上，采样频率为1 kHz。下面分别给出采用常规方法和旁瓣重合法设计的符合上述要求的FIR带通数字滤波器在Matlab平台上仿真的频响曲线和各阶次谐波的幅度表。常规方法设计满足以上要求的基于高斯噪声分布的FIR低通数字滤波器，最低阶次为213，其频响如图(1-a)所示。

图1 常规方法与旁瓣重合法滤波器频响曲线

而采用旁瓣重合法设计，滤波器的阶次为19即可满足以上要求，其频响如图1-b所示。两种滤波器对各阶次谐波的衰减幅度如表1所示，从表1可以看出，后者对基波有一定衰减作用，但对各次谐波的衰减与对基波的衰减之差明显比前者大，即滤波之后的信号信噪比优于前者，而阶次远低于前者。

表1 两种方法对谐波衰减程度的对比

2.3 信号分析

根据对牵引网电力信号的统计结果，构建模拟的电力信号:

式(9)信号波形和经优化滤波器处理后的波形如图2所示;对式(9)对应信号经优化滤波器处理前、后进行频谱分析，其频谱分别如图3所示。

图2 滤波前、后的信号波形

图3 滤波前、后的信号频谱

3 结束语

以上分析了FIR数字滤波器频响的振荡特性及其产生的原因，并结合电力系统中噪声主要为谐波信号的特点，给出了在保证频响满足要求的前提下，可显著降低滤波器阶数的优化方法。通过在Matlab平台上仿真，证明了这种方法的有效性。

［1］ 芮坤生.信号分析与处理［M］.中国:高等教育出版社，1993:82.

［2］ Mohand Mokhtari，Michel Marie.MATLAB与SIMULINK工程应用［M］.中国:电子工业出版社，2002: 132.

［3］ 张登奇，李望移.基于MATLAB的FIR数字滤波器设计［J］.计算机时代，2007(11).

［4］ 李洋洋，江亮亮.基于MATLAB的FIR数字滤波器的设计与实现［J］.黑龙江科技信息，2008(27).

［5］ 汝晓艳，时玲.基于FIR数字滤波器的Matlab设计［J］.现代电子技术，2007(17).

Optimized Method of FIR Digital Filter Based on Electrical Signal

CHEN Bang-qiong (Department of Computer，Chien-shiung Institute of Technology，Taicang 215411，China)

By analyzing the characteristics and the cause of the FIR digital filter＇s frequency loud vibration，combining with its application in electrical power system，the article expounds an optimized method-side lobe coincidence method.The method can guarantee frequency sound，satisfy the request，and obviously reduce the filter exponent number.It is proved to be valid by simulating in the Matlab/Simulink platform.

FIR;Digital filter;window function;Side lobe coincidence

book=29,ebook=29

TN 713

B

1672-2434(2010)03-0019-03

2010-04-02

陈邦琼(1968-)，男，讲师，硕士，从事研究方向:信号与信息处理