丢番图方程x3+x2+x=y2-4y+3的整数解

施俊

(江苏技术师范学院数理学院 江苏常州 213001)

丢番图方程x3+x2+x=y2-4y+3的整数解

施俊

(江苏技术师范学院数理学院 江苏常州 213001)

利用奇偶分析、因式分解等初等方法证明了丢番图方程x3+x2+x=y2-4y+3的整数解为:(x，y)=(-1，2)，(0，1)，(0，3)，(1，4)，(1，0)，(7，22)，(7，-18)。

整数解;因式分解;奇偶分析

丢番图方程的问题主要值得研究的是:

①是否有解?

②有解时有多少解?解数是有限还是无穷?

③求出全部解。

解决丢番图方程的主要方法有:

①代数式的恒等变形(包括分解因式);

②估计;

③同余(包括奇偶分析);

④无穷降阶法;

⑤ 其它［1］。

这里在前人的一些结论基础上利用初等方法讨论证明一个丢番图方程的整数解。

引理1［2］:

①丢番图方程x4+y4=z2仅有xy=0的整数解;

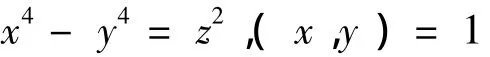
②丢番图方程仅有整数解x2=y2=1和x2=1，y=0。

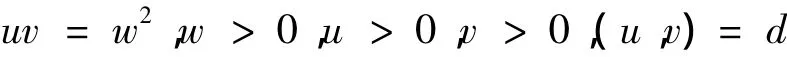
引理2:丢番图方程的一切正整数解可以写成:

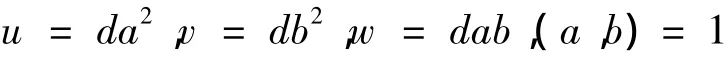
于是

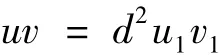
而

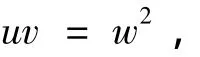
故

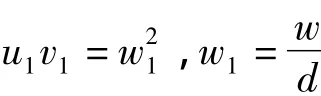
由

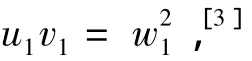
有

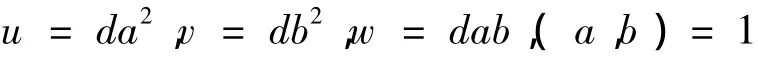
下面讨论方程的整数解.

定理:丢番图方程

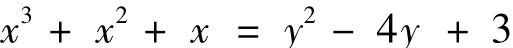
的整数解:

证明:方程变形为

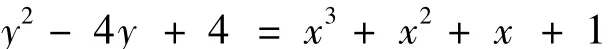
即

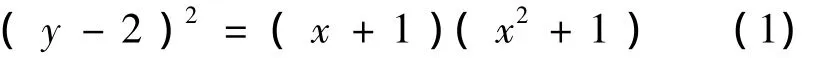
显然x≥ -1，将x=-1，0，1代入原方程得出y的值，则得解:

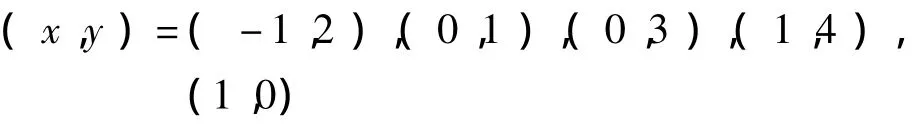
1)若x为大于0的偶数时

由

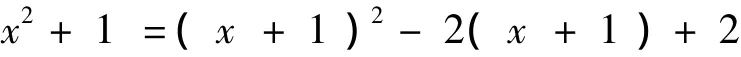
易知

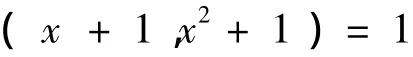
由(1)式可得［3］

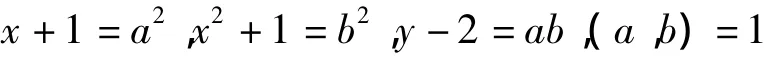
但x2+1=b2只有解x=0，进而y=1，3，这两组解上面已出现。

2)若x为大于1的奇数时

此时可得到

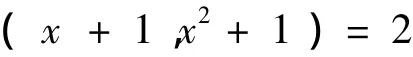
由(1)式及引理2可得

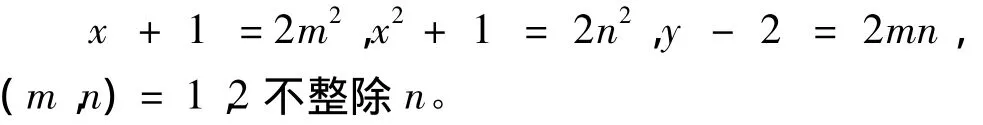
由

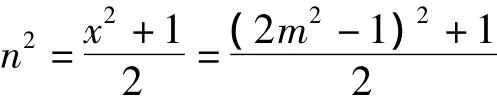
可得

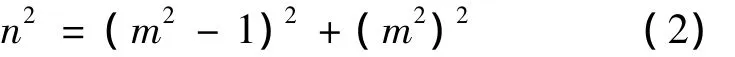
①当m为奇数时

由(2)式可得［3］

m2=u2-v2，m2-1=2uv，n=u2+v2，其中一奇一偶，(u+v，u -v)=1。

由

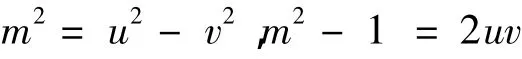
有

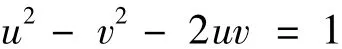
再由

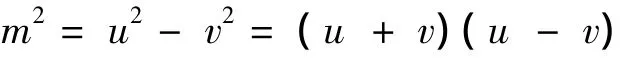
得到［3］

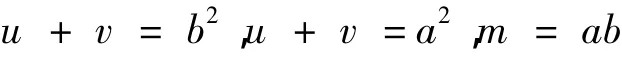
进而

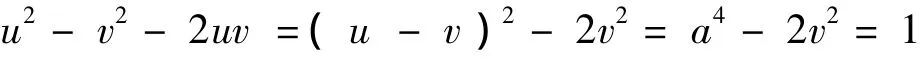
即

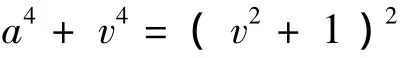
但由引理1知此方程无整数解，因此，当m为奇数时式(2)无整数解，从而原方程无整数解.

②当m为偶数时

由(2)式可得［3］

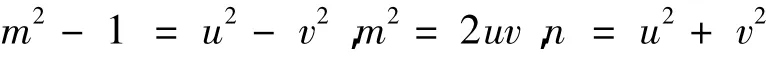
由

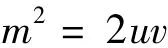
可推得

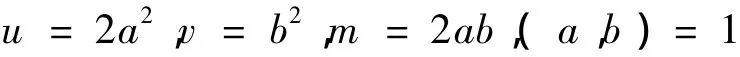
或

不妨设

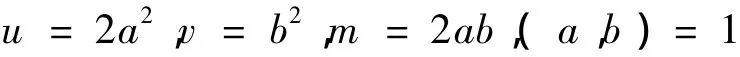
成立，由

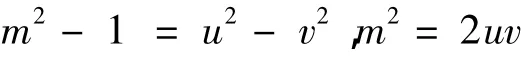
有

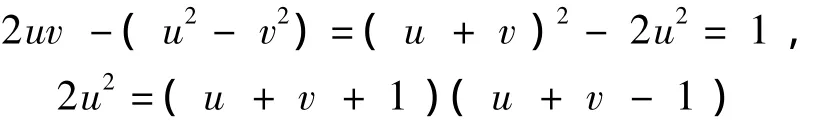
因为u，v一奇一偶，故可设

又因

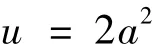
则有

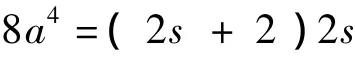
即

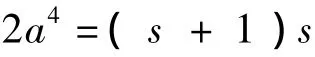
当s为偶数时，由(s+1，s)=1知

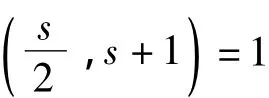
于是

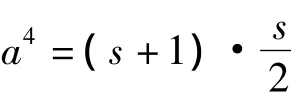
进而有［4］

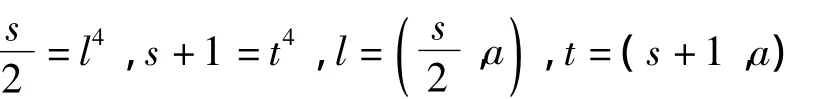
且易知

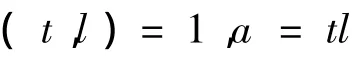
当s为奇数时同理有

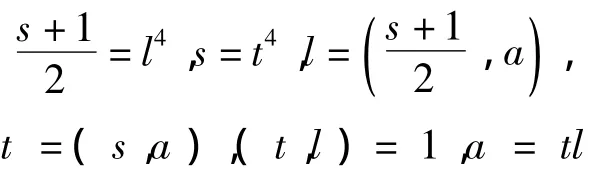
故有

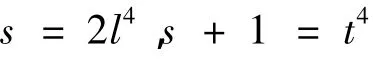
或

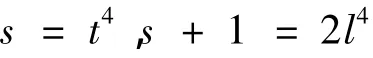
其中

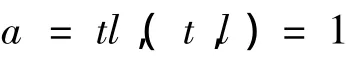
所以，

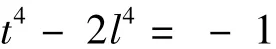
或

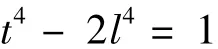
即

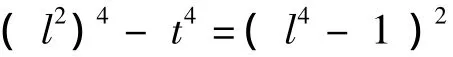
或

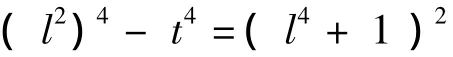
a)讨论方程

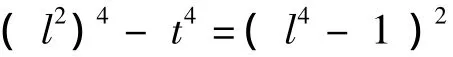
由引理1可知

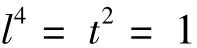
和

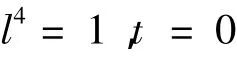
显然

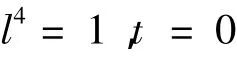
不成立，则考虑

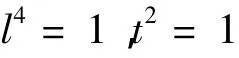
若l4=1，由

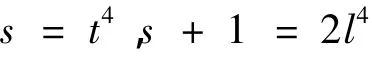
给出

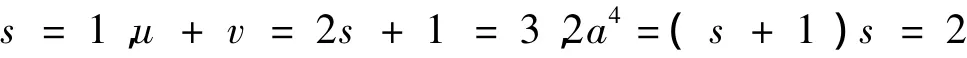
则有

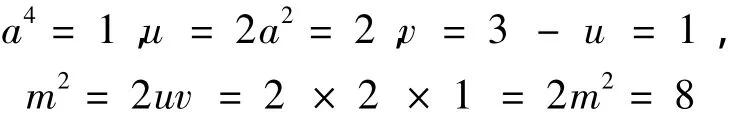
通过代入(1)式得

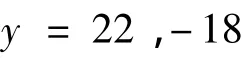
b)讨论方程

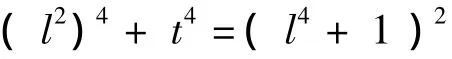
由引理1可知其无非零整数解.显然t4=0不成立，而l2=0时，则由

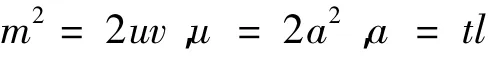
知m=0矛盾

故当m为偶数时原方程只有整数解:

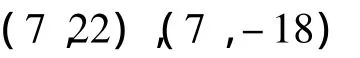
综合上面得出原方程

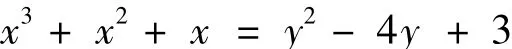
只有整数解:

［1］ 单墫.数学竞赛研究教程［M］.南京:江苏教育出版社，1993:153.

［2］ 曹珍富.丢番图方程引论［M］.哈尔滨:哈尔滨工业大学出版社，1989:26-28.

［3］ 闵嗣鹤，严士健.初等数论［M］.3版.北京:高等教育出版社，2003:35.

［4］ 潘承洞，潘承彪.初等数论［M］.北京:北京大学出版社，1992:35.

The Integer Solutions of the Diophantine Equations x3+x2+x=y2-4y+3

SHI Jun
(Faculty of Mathematics and Physics，Jiangsu Teachers University of Technology，Changzhou 213001，China)

By using odd and even analysis and indeterminate equation etc primary methods，we have proved that the Diophantine Equations x3+x2+x=y2-4y+3 has only the integer solutions(x，y)=(-1，2)，(0，1)，(0，3)，(1，4)，(1，0)，(7，22)，(7，-18).

integer solution;indeterminate equation;odd and even analysis

book=23,ebook=23

O 156.7

A

1672-2434(2010)03-0016-03

2010-04-19

施 俊(1976-)，男，讲师，硕士，从事研究方向:代数数论