马尔可夫链在教学质量评估中的应用研究

施政

(炎黄职业技术学院基础部 江苏淮安 223400)

马尔可夫链在教学质量评估中的应用研究

施政

(炎黄职业技术学院基础部 江苏淮安 223400)

对马尔可夫链在教学质量评估中的应用进行了研究，阐明了这种方法的基本原理及其具体实施步骤，为合理、有效地评价教学效果提供理论和实践依据，并说明了马尔可夫链评估法在评估教学质量时较其它评估方法更具合理性。

马尔可夫链;平稳分布;转移矩阵;教学质量

在进行教学质量评估方法中，传统的方法主要是分析学生某次考试成绩的平均分或者及格率等，甚至以此作为主要依据来判断各个不同班级不同任课教师的教学水平。其实，这是不合理的，除非不同的班级基础、教学环境等完全一样。本文利用马尔可夫链基本原理，尝试剔除学生原有基础对教学质量评价的影响，以期得到比较合理的教学质量评估方法和结论。

在以往关于马尔可夫链分析法在教学质量评估中应用的文献中，学生成绩的分类法基本上是以分数线作为分类方法，本文尝试从名次的角度进行分类，以期得到比较好的结论。

1 马尔可夫链的基本思想

“过去只影响现在，而不影响将来”，这种随机过程称之为马尔可夫过程。时间离散、状态离散的马尔可夫过程称之为马尔可夫链。

下面给出相关数学定义:设(Ω，F，P)为一概率空间，{Xn，n≥0}是定义在其上的取值为整数的随机序列，如对任意的m≥1及非负整数有其中其中为{Xn，n≥0}的状态空间，且假定等式两端的条件概率都有意义，则称{Xn，n≥0}为马尔可夫链。

设{Xn，n≥0}为齐次马尔可夫链，若对一切状态i，j，存在不依赖于i的常数πj，使得

则称马尔可夫链{Xn，n≥0}具有遍历性。

2 马尔可夫链在教学质量评估中的原理与方法

在教学质量评估中为了去除学生基础成绩的影响，可以使用马尔可夫链分析法来进行讨论。按照一定的方法将学生成绩分级，这样就可以确定统一的状态空间，然后由相关等级变化来确定一步转移矩阵，利用马尔可夫链的平稳性和遍历性求出极限向量，最后利用极限向量值进行比较判断。

具体来说:在教学质量指标量化过程中，运用马尔可夫链法将两个班级的学生第一次考试成绩放在一起按高低分划分为s个等级，然后计算出各班在各等级学生人数与各等级人数之比作为状态向量，用A表示:

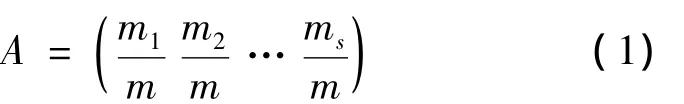
其中，m为学生总人数，mj为第i(=1，2，…，s)等级的学生人数。

经阶段教学后，把测得的学生成绩合在一起也按照高低分划分为s个等级，然后分析上述两个班各等级学生在阶段教学后等级变化情况，从而求出一步转移矩阵p:

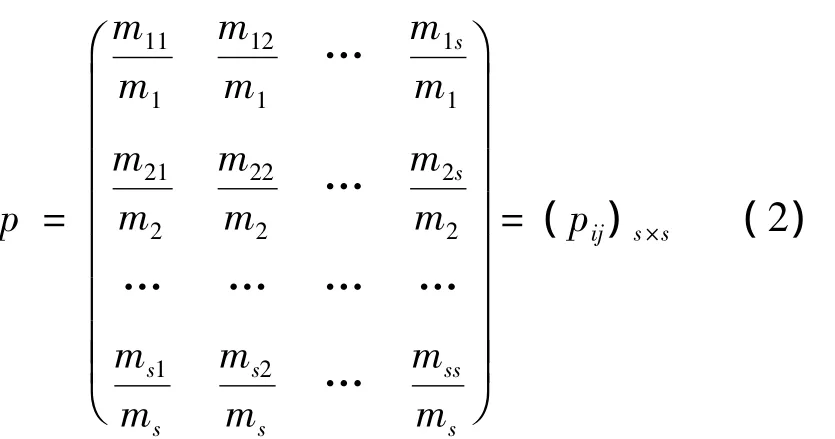
其中，mi仍表示开始的第i等级中的学生数，mij表示阶段教学后属于第i等级的学生其成绩转移到第j等级的学生数，且满足

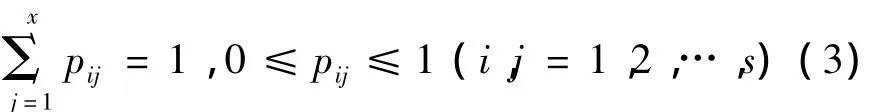
若研究多步(n＞1)转移概率P(n)，由切普曼-柯尔莫哥洛夫方程(C-K方程)得

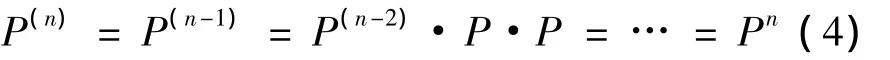
当n→∞时，如果马尔可夫过程所涉及的各状态的概率分布稳定不变，由遍历性，建立方程组

得到极限分布

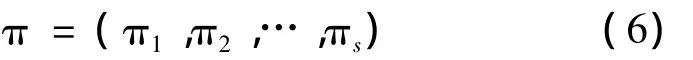
据此，可求出稳定的概率向量，这个稳定的概率向量就成为评价标准，然后通过求解方程组得到具体的量化指标。通过得到的量化指标可以比较客观地对教师教学质量进行评估。

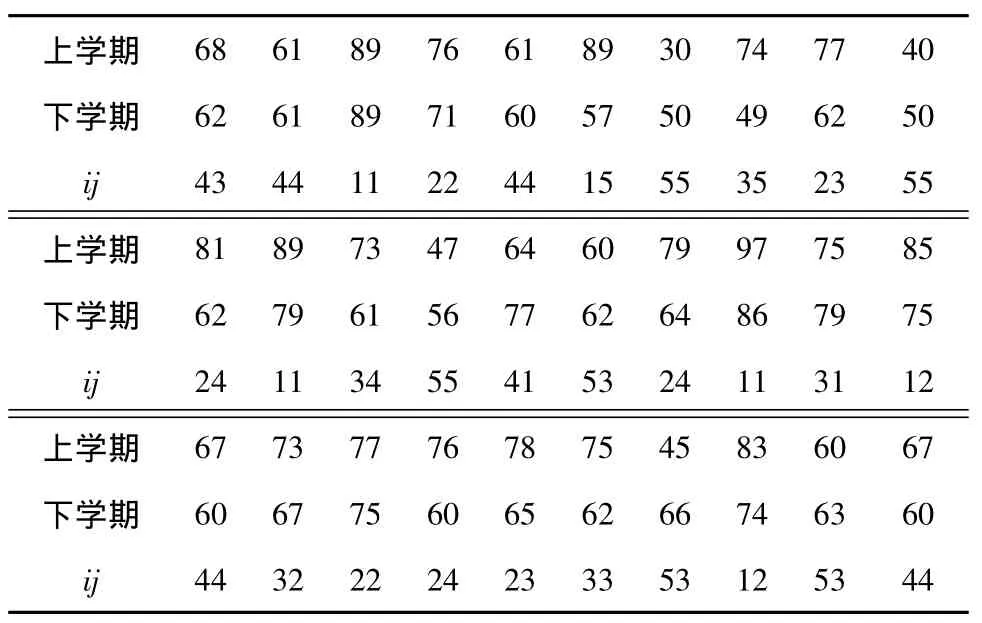
表1 某学年A班考试成绩及等级转移情况

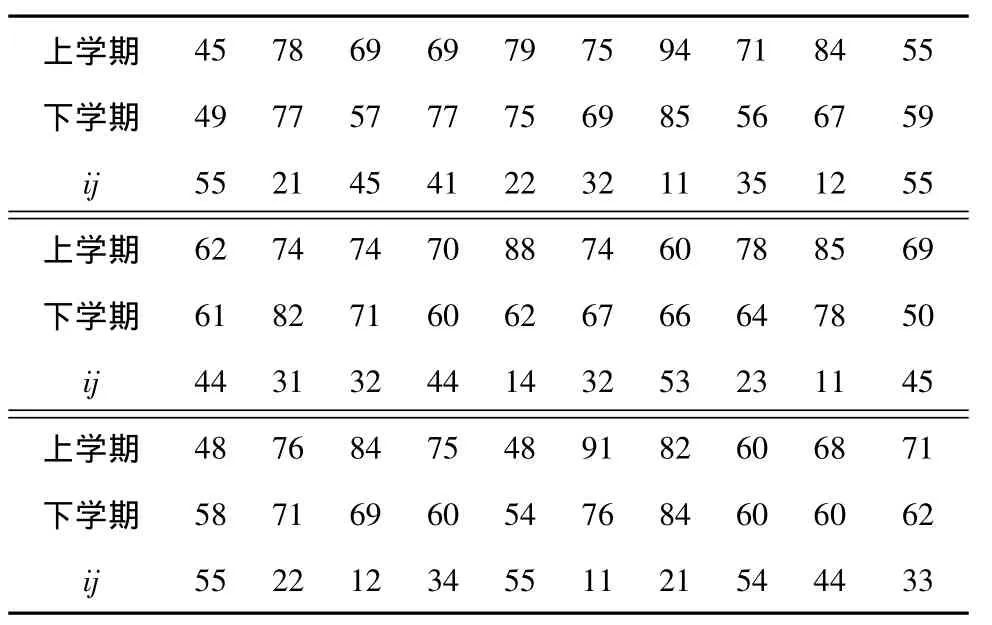
表2 某学年B班考试成绩及等级转移情况

3 马尔可夫链在教学质量评估中的实例分析

实例分析如何运用马尔可夫链分析法对教师的教学质量进行评估。

设某高职院校某专业一年级A、B两个班，每个班各有30名学生，从下学期开始由不同教师担任高等数学的教学工作，两个班本学年的上、下两学期高等数学期末考试成绩分别如表1、2所示，其中ij为某学生成绩从第i等级转移到第j等级(这里i，j= 1，2，…，5状态，“1”为第1～12名;“2”为第13～24名;“3”为第25～36名;“4”为第37～48名;“5”为第49～60名)，分别表示A、B两个班级上学期成绩为第i等级的学生数，分别表示A、B两个班级中上学期成绩为第i等级，下学期成绩转到第j等级的学生数。

对上述两个班学生上、下学期成绩分别进行排名，且在表1、2中给出了等级转移情况，由此可以得到两班的一步转移概率矩阵(用PA、PB分别表示A、B班的一步转移概率矩阵):

利用Mathematica软件计算得，

同样计算得，

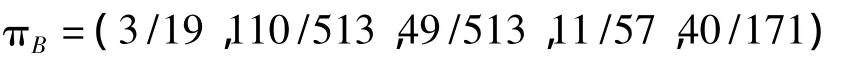
根据所求得A、B两个班的极限向量πA和πB，按最大概率原则，可以预测，A班的教学质量将达到第“4”等级，而B班的教学质量将达到第“1”等级。若对远期的整体情况进行评估，可取如下等级分，1分(“1”级)，2分(“2”级)，3分(“3”级)，4分(“4”级)，5分(“5”级)，则两个班的预期等级分别为:

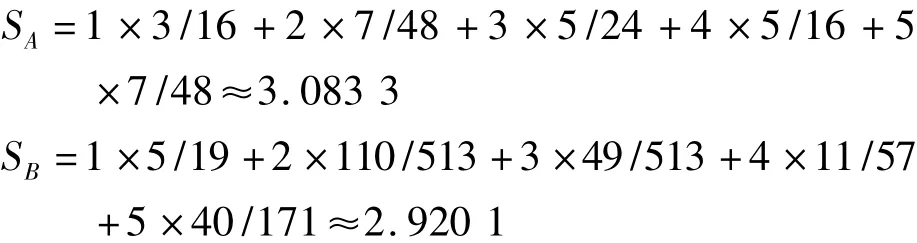
由SA＜SB，可见B班学生成绩的转移情况要好于A班学生成绩的转移情况，在一定程度上也说明了，B班高等数学任课教师的教学质量要高于A班高等数学任课教师的教学质量。

这个例子，如果这样来思考:A班上学期平均分为70.53分，下学期平均分为65.47分，总体平均下降了5.06分。B班上学期平均分为71.87分，下学期平均分为66.20分，总体平均下降了5.67分。如果通过下降分来比较，5.06分＜5.67分，就断言A班的高等数学任课教师的教学质量要高于B班高等数学任课教师的教学质量，显然这样的分析方法有失科学性。因为有可能极个别学生两次考试的分数出现异常的波动，而严重影响上面的平均分差。

另外，这个例子在数据分类时，如果采用分数线分类法，也不是很理想，因为在分类过程中，以分数线来划分，往往没有考虑到在同一分数段内名次的差异，因为在两个同类班级的比较中，比如说前10名某班占多少名，前20名某班占多少名等，更能说明某班整体水平的情况。如果按照文献［1］～［4］的分类方法，且采用同样的计算方法，得SA=60.66分 ＞50.00分 =SB，于是得到A班的高等数学任课教师的教学质量要高于B班高等数学任课教师的教学质量这样的结论，显然也和本文结论相左。

在日常工作中，经常需要讨论类似于教学质量评估等问题，在讨论中同样也涉及到事情原有基础问题，此类问题都可以尝试用马尔可夫链分析法来进行讨论。

［1］ 彭梅.随机过程在教学质量评估中的应用［J］.安庆师范学院学报:自然科学版，2006(3):32-35.

［2］ 刘亚欣，扎那.马尔可夫链在教学评价中的应用和改进［J］.大连铁道学院学报，2006(2):5-8.

［3］ 孙景艳.马尔可夫链在教学评价中的应用［J］.河南师范大学学报:自然科学版，2008(2):10-13.

［4］ 冯虹，等.马尔可夫链在教学质量评价中的应用［J］.天津师范大学学报:自然科学版，1999(1):5-9.

Application of Markov Chain Method in Teaching Evaluation

SHI Zheng
(Department of Basic Course，Progenitor College，Huai＇an 223400，China)

This paper studies the application of Markov Chains in teaching evaluation.It expounds its principle and application procedure and provides evidences both in theory and practice for its reasonable and effective evaluation in teaching.And it also proves that the Markov Chains method is better than others in teaching quality evaluation.

Markov Chains;stationary distribution;transfer matrix;teaching quality

book=20,ebook=20

G 712.0

A

1672-2434(2010)03-0010-03

2010-04-28

施 政(1977-)，男，讲师，硕士，从事研究方向:应用统计学