非线性的双目数码成像定位模型

杨新平 周彩菊 晏 龙 李 斌

(楚雄师范学院数学系,云南 楚雄 675000)

非线性的双目数码成像定位模型

杨新平 周彩菊 晏 龙 李 斌

(楚雄师范学院数学系,云南 楚雄 675000)

利用透视对应链的观点建立双目定位的非线性模型,该模型参数实际含义清楚明了,表达式直观准确,数据计算简单流畅,具有很强的创新性。

双目视别;射影对应;透视;空间定位

1 引言

随着社会、政治、经济环境的发展,对每一个家庭或部门而言,生产及人身安全问题日益成为一个严重的社会问题。解决这个问题现有的主要方法和手段通常是在不同空间区域设置一些数码摄像机,通过数码双目计算机视觉的自适应识别系统,得到了两幅二维图像,应用计算机图像处理、图像匹配、三维重建等方法,实现从二维图像恢复为场景的三维图像。这是一种模拟人的双目视觉的方法,将此方法应用于现有监控系统,能在很大程度上消除安全隐患问题。

80年代美国麻省理工学院人工智能实验室的Marr提出了一种视觉计算理论,并将其应用在双目匹配技术上,这项技术可以通过两张有视觉差异的平面图产生有深度的立体图形,它为双目立体视觉发展理论奠定了基础。目前双目计算机视觉识别技术不仅只是用于监控管理,而且因为它的高效性和易操作性使得这项技术在社会各个领域得到了广泛运用。基于这样一个应用背景,对于与这项技术相关联的数学问题就成为一个很有研究价值的课题,同时也是一个难题,相应问题的解决可以为计算机的模拟及图形识别提供数学理论依据。

相机成像定位模型从现有文献资料来看,分成线性模型和非线性模型两种,文献 [1]解决了机械手抓取目标物的空间位置的确定问题,达到了相应的精度要求。文献 [2]解决了摄像机参数的标定方法,并把标定的参数和出厂参数作了比较。类似的文章较多,但大多数文献均是基于已有的数学模型 (1)展开讨论的,并且大量已有文献,都是在参数矩阵已知或半已知的情况下才开展研究的。该模型属于射影几何中的线性模型:

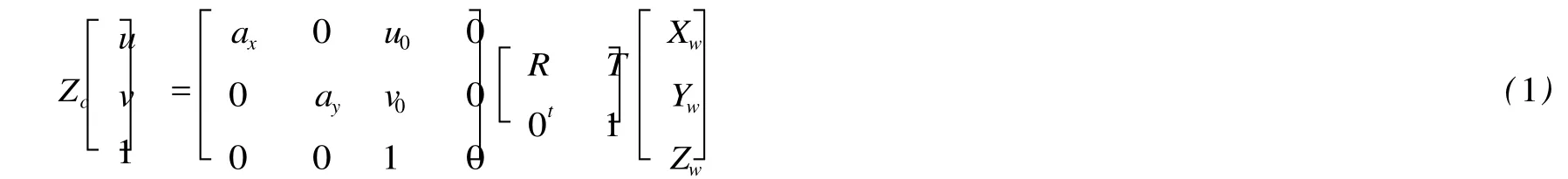
至于非线性模型,文献[3]中用几何综合法建立了一个非线性模型,但该模型中表达式比较复杂,阅读困难,难以理解,图形直观性也不够。

本文采用空间解析几何的思想,结合射影几何的有关知识,用透视链的观点建立了双目定位的非线性模型,该模型参数实际含义清楚明了,表达式直观准确,数据计算简单流畅,这是本文与其他文章的最大差别也是本文的最大创新。

2 非线性模型的建立

实际应用中常用两部相机来定位,对于物体上一个特征点,用两部固定于不同位置的相机摄得特征点的像,分别获得该点在两部相机像平面上的坐标。当知道两部相机的相对位置时,就可用几何的方法得到该特征点空间位置坐标。

如在十字路口设置的交通监管(电子警察),就是用两台像机确定违章车辆的位置。通过对电子警察观察后发现,用于摄像的两部相机,有一部在放置时,基本上保证光轴线与路的中间分界线平行,可以照得车辆的正面车牌照片,另一部在放置时,光轴线往往与路的中间分界线有一个角度,目的是通过该像机拍到违章车辆的侧面像片,从而通过计算机视觉的自适应识别技术,还原违章车辆的空间位置。根据这一点作出模型假设:

(1)两台相机的配置完全一致,拍摄环境对相机的拍摄效果不产生影响。

(2)两台相机相对于地面的高度是等高的。

(3)固定第一台相机的拍摄位置时,尽最大可能保证它的光轴线平行于路的中间分界线从而也就垂直于靶标面(被拍目标物的特征点所在平面)。

在建立模型之前,为了更清楚阐述建模的思想,先在平面上讨论两台平行放置的照相机模拟人类视觉空间定位的数学原理(图1)以两台相机的光心A,B为原点,平面 EC和DF分别为成像平面,特征点 H在两像平面上的像分别是 C,D,两像机的光轴线此时垂直于靶标面MHZ,这是理想状态,实际情况是有一台相机的光轴线斜对着靶标面。如果知道像点 C,D坐标,建立求解 H在坐标系A-xzy下的空间坐标(x,z,y)的数学模型。

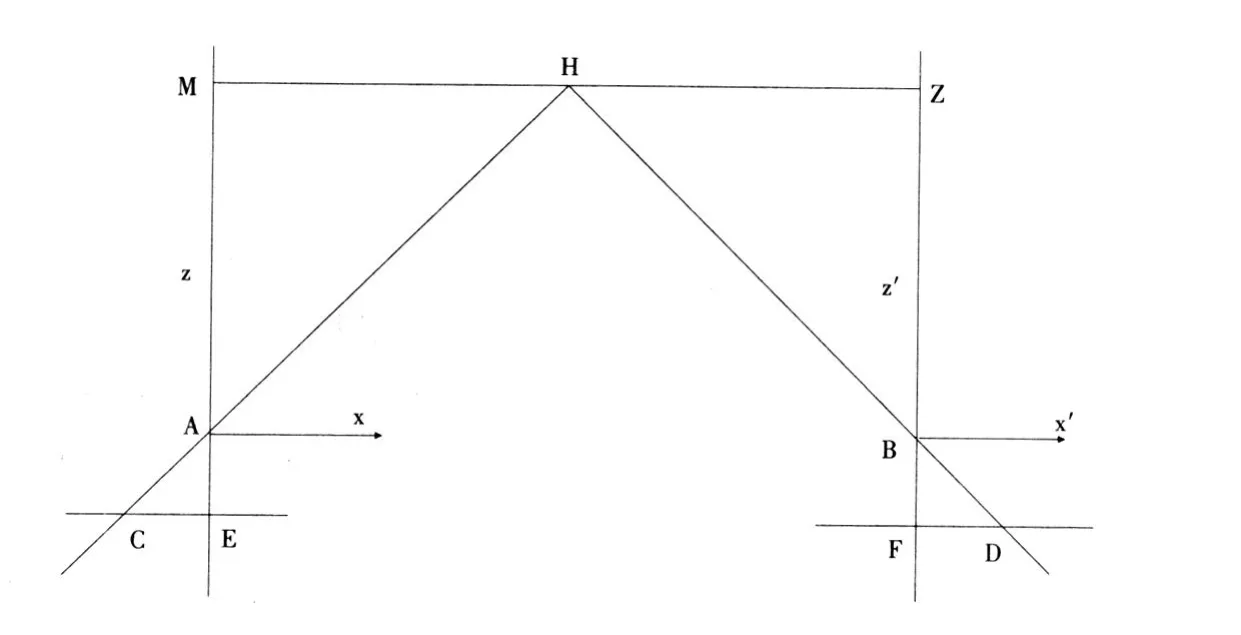
图1 双目立体视觉成像原理

根据这一原理,我们将两个相机的空间成像透视原理绘制成图(图2)。该图详细刻画了两台相机成像的射影原理,这是本文解决问题的关键。

设靶标所在平面为 PMH,Q为靶标面上实物点 P在A相机(A也代表A相机的光心)的成像面上的像,Q′为靶标面上实物点P在B相机(B也代表B相机的光心)的成像面上的像,P在垂直于成像平面的水平面MHCE(在两相机等高的假设之下,MHCE平面正是A,B及它们的光轴线交点O确定的平面AOB)上投影为H,Q在MHCE面上的投影为C,C就是实物点H在A相机的像平面上的像,过A作靶标面 PMH的垂线,垂足为M,交像平面于 E,E为M的像。所以EQC就为实物M PH在A相机的像平面上的像,它们构成一个以A为中心,A相机的像平面与靶标面的一个透视对应关系,三角形 EQC为三角形M PH的透视三角形。同理,Q′在MHCE面上的投影为D,D就是实物点 H在B相机的像平面上的像,F为M在B相机的像平面上的像。在两相机等高的假设下,MHCE平面与MHDF平面是同一平面,三角形FQ′D为三角形M PH的第二组透视三角形。两次透视构成了一个透视对应链。由射影几何的定理可知,两次透视形成一个射影对应,将A相机的像平面上的像点映射成B相机的像平面上的像点。本文就是根据这一原理建立一个非线性的数学模型,通过该模型可以由两张像平面上点的坐标,定位出空间特征点的坐标。

首先以A相机的光心为原点建立空间坐标系,光轴方向AM为z轴,xAy平面平行于A相机的像平面,建立第一个右手坐标系A-xzy,固定A相机的位置后,选定空间适当位置O点为中心,以适当长 R为半径绕O在平面MHCE内旋转一个角度β,确定位置B。(需要一个有拍摄经验的人参与确定)在B点设置第二台相机,光轴方向沿BO方向,对靶标面 PMH进行拍摄,两台相机的光轴交于O点,从而平面MHCE与平面AOB是同一个平面。

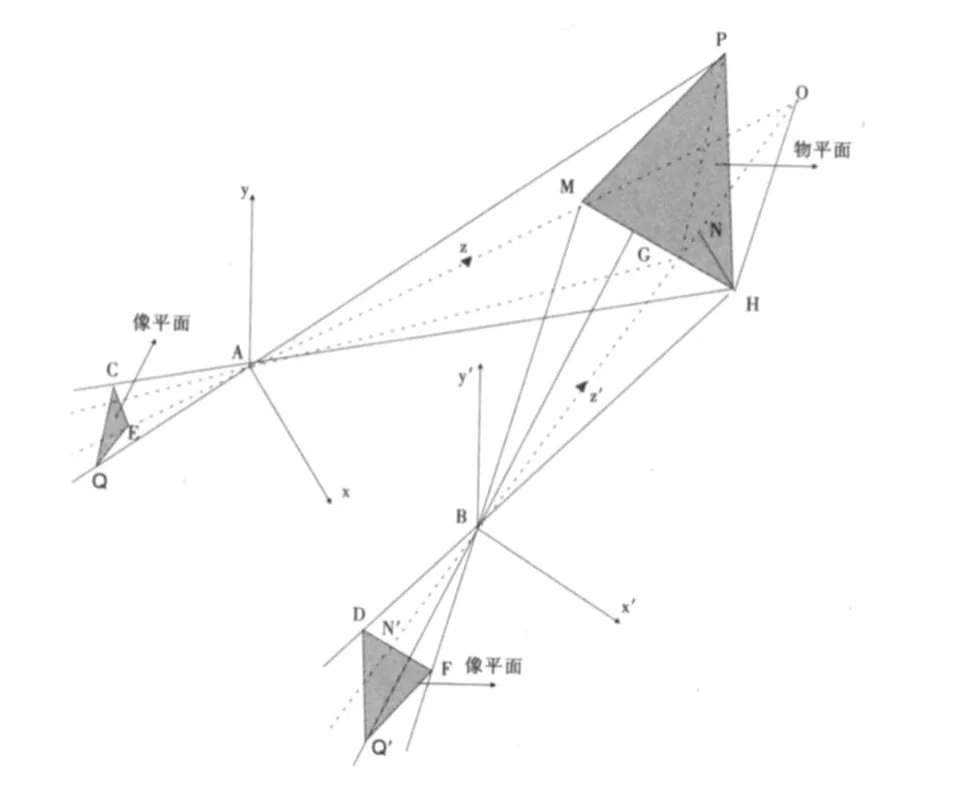
图2 两部相机空间成像原理图

这样从两个位置实现了对靶标面 PMH同时进行照相,所成的图像为三角形 EQC及三角形 FQ′D。记 ∠AOB=β,以B相机的光轴方向为 z′轴,x′B y′平面平行于B相机的像平面建立第二个右手坐标系B-x′z′y′(图 2)。

在该射影对应中,对于相机A来讲,由于QC垂直于MHCE面,PH垂直于MHCE面,所以, QC∥PH。又因为光轴方向AM(z轴)垂直于靶标面 PMH,光轴方向AM又垂直于A相机的像平面,所以A相机的像平面就平行于靶标面 PMH。从而有:

在实际拍照过程中,正好相当于A相机的镜头正对着靶标面进行拍照,如前面所述的电子警察一样,A相机这样设置是合理的。

在两坐标系 A-xzy及 B-x′z′y′下,设 C(x0,z0,0),H(x,z,0),P(x,z,y),Q(x0,z0,y0), Q′(x′,z′,y′)由 (2.1)得

由透视仿射知识可知,点 H在B相机像平面上的成像点是D(x′,z′,0)过H作HN⊥BO, NH在平面MHCE上。

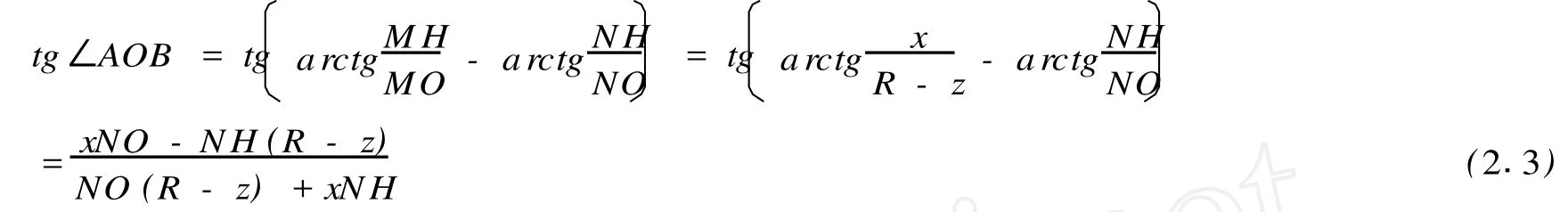
对于B相机,由物理知识可知,像距z′、物距BN具有下列关系(因为N的像是

数码相机 B拍照时,所成的相为实像,由物理学知识可知:z′>f,上式是有意义的。将(2.5)代入(2.4)得NH

对于A相机,由物理知识可知,像距 z0,物距AM=z具有下列关系(因为M的像是 E):数码相机A拍照时,所成的相也是实像,由物理学知识可知:z0>f,上式是有意义的。

将(2.6)、(2.7)式代入(2.3)整理得:

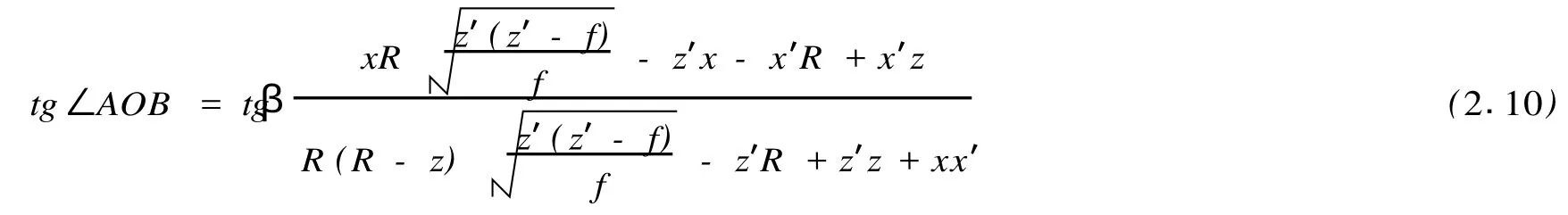
综合(2.8)、(2.9)、(2.10)得双数码相机的空间定位的非线性模型:

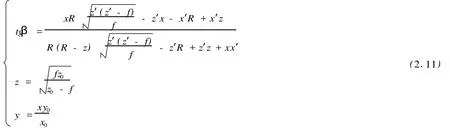
其中 f为两相机的焦距,相机取定后它的值自然知道。如果两台相机焦距不同,设A相机与B相机的焦距份别为 f1,f2,只要对模型(2.11)中的 f稍加改动,数学上的推导不变,就得到相应的模型(2.12)。

3 模型求解和评价

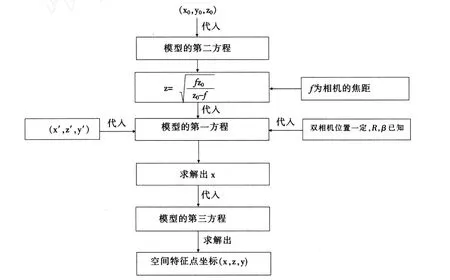
图3 模型求解流程图

(1)两台相机拍摄同一个特征点后得到两张相片,从两张相片上得到两个像点的坐标,分别记为 (x0,z0,y0)、(x′,z′,y′),由相机在设置时的具体位置可以知道R及β的值,按照图3的计算步骤进行计算,最终得到空间特征点的坐标 (x,z,y)。在数学软件Matlab环境下,将上述坐标按图 3所示流程,依次代入模型(2.11),可以非常容易地计算出空间特征点的坐标。

(2)在非线性模型中,参数R,β实际含义清楚明,模型的表达式直观、准确,模型的数值计算非简单,实际应用中有很强的可操作性。在设置两台相机相对位置时,需要确定一个适当的位置点O、半径 R、转角β,需要一个有实际摄影经验的人员参与这项工作。

(3)由于缺少位于不同位置的两部相机实际拍摄的两张照片,相应的坐标数据也就无法获得,所以无法进行实证分析,这是本文的一个缺陷。但这不影响文中严格的数学推导和数学技巧。实证部分就只能由相关领域的人员在具有第一手资料的基础上展开进一步讨论。

[1]田正冲,乌日图,王飞 .基于射影几何的目标点三维坐标值测量 [J].机械工程与自动化,2007(5):24—28.

[2]蔡健荣,赵杰文 .双目立体视觉系统摄像机标定 [J].江苏大学学报 (自然版), 2006,27(1):7—9.

[3]罗亚波,陈定方 .采用射影几何方法实现视觉模拟系统 [J].武汉理工大学学报, 2002,24(8):83—85.

[4]朱德祥,朱维宗 .高等几何 (第二版)[M].北京:高等教育出版社,2007.

[5]张之江,于庆兵,张智强 .双摄像机靶标成像视觉坐标测量方法研究 [J].测试技术学报,2004,18(4):305—310.

[6]霍光,刘荣 .双目立体视觉在光电子器件自动对接系统中的应用 [J].军民两用技术与产品,2007(3):42—44.

[7]石辛民,郝整清 .基于 MATLAB的实用数值计算 [M].北京,清华大学出版社.2006.

[8]李葆春 .再谈小孔成像 .六盘水师专学报 [J].2000,12(1):15—17.

[9]苏中,夏艳,吴细宝 .基于激光双目视觉系统的直径测量 [J].半导体光电, 2008,29(1):131—139.

(责任编辑 刘洪基)

The NolinearM odel of Binocular D igital I maging Location

YANG Xin-ping;ZHOU Ca i-ju;YAN Long;L I Bin
(Department of M athematics,Chuxiong N or m al University,Chuxiong675000,China)

There are two topics in the CUMCM in 2008(China Undergraduate Mathematical Contest inModeling)which are A and B problems.A topic is about binocular digital imaging location.It is very difficult to solve this problem,and needs clever mathematical skills.Based on the viewpoint of perspective correspondence link,this paper sets up a nolinearmodel of binocular visual location which actualmeaning of parameter is very clear,analytic formula is audio-visual and exact and calculation is simple and easy.The model is new and original.

binocular visual recognition;projective transform;perspective;spatial location.

O224

A

1671-7406(2010)03-0026-06

2009-11-23

杨新平 (1969—),男,云南姚安人,讲师,主要从事数学教学与研究。