线性距离空间构成赋范线性空间和内积空间的充要条件

郎开禄

(楚雄师范学院数学系,云南 楚雄 675000)

线性距离空间构成赋范线性空间和内积空间的充要条件

郎开禄

(楚雄师范学院数学系,云南 楚雄 675000)

本文给出线性距离空间构成赋范线性空间的一个充要条件和线性距离空间构成内积空间的三个充要条件。

线性距离空间;赋范线性空间;内积空间;充要条件

赋范线性空间一定可以赋予距离构成线性距离空间,但线性距离空间不一定能赋予范数构成赋范线性空间;内积空间一定可以赋予范数构成赋范线性空间,从而内积空间可以赋予距离构成线性距离空间,但赋范线性空间不一定能赋予内积构成内积空间,从而线性距离空间不一定能赋予内积构成内积空间。本文给出线性距离空间构成赋范线性空间的一个充要条件和线性距离空间构成内积空间的三个充要条件。

1 线性距离空间构成赋范线性空间的充要条件

定理 1[1][2][3]若 (x,‖·‖)是赋范线性空间,则 (X,d)是线性距离空间,其中 d(x,y) =‖x-y‖,x,y∈X,反之,则未必然。

定理 2[1]若(X,d)是线性距离空间,则(X,‖·‖)是赋范线性空间的充要条件是

(1)d(αx,0)=|α|d(x,0);(2)d(x-y,0)=d(x,y)。其中 ‖x‖ =d(x,0),x,y∈X, α∈K。

定理 3[2][3]若(X,d)是线性距离空间,则(X,‖·‖)是赋范线性空间的充要条件是

(1)d(αx,0)=|α|d(x,0);(2)d(x+z,y+z)=d(x,y)。其中 ‖x‖ =d(x,0),x,y,z∈X,α∈K。

本文给出线性距离空间构成赋范线性空间的一个充要条件:

定理 4 若(X,d)是线性距离空间,则(X,‖·‖)是赋范线性空间的充要条件是

(1)d(αx,0)=|α|d(x,0);(2)d(x+y,0)≤d(x,0)+d(y,0)。其中 ‖x‖ =d(x,0), x,y∈X,α∈K。

证明:(⇒)设(X,‖·‖)是赋范线性空间,则

(1)d(αx,0)=‖αx‖ =|α|‖x‖ =|α|d(x,0);

(2)d(x-y,0)=‖x-y‖ =d(x,y)。

(⇐)令 ‖x‖ =d(x,0),x∈X,则

(Ⅰ)‖x‖ =d(x,0)≥0,且 ‖x‖ =0⇔d(x,0)=0⇔x-0;

(Ⅱ)‖αx‖ =d(αx,0)=|a|d(x,0)=|α|‖x‖;

(Ⅲ)‖x+y‖ =d(x+y,0)≤d(x,0)+d(y,0)=‖x‖+‖y‖。

故(X,‖·‖)是赋范线性空间。

2 线性距离空间构成内积空间的充要条件

定理 5[1][2][3](Ⅰ)若 (X,〈·,·〉)是内积空间,则 (X,‖·‖)是赋范线性空间,且

‖x+y‖2+‖x-y‖2=2(‖x‖2+‖y‖2),其中

(Ⅱ)若 (X,‖·‖)是赋范线性空间,且范数 ‖x‖满足 ‖x+y‖2+‖x-y‖2= 2(‖x‖2+‖y‖2),则在 (X,‖·‖)中可定义内积〈x,y〉:

本文给出线性距离空间构成内积空间的三个充要条件。

定理 6 (Ⅰ)若 (X,〈·,·〉)是内积空间,则 d2(x,y)+d2(x,-y)=2(d2(x,0)+d2(0, y))。其中

(Ⅱ)若 (X,d)是线性距离空间,且

(1)d(αx,0) =|a|d(x,0);(2)d(x-y,0) =d(x,y);(3)d2(x,y)+d2(x,-y) = 2(d2(x,0)+d2(0,y))。

则(X,〈·,·〉)是内积空间,其中

证明:(Ⅰ)若(X,〈·,·〉)是内积空间,由定理5(Ⅰ)知,(x,‖·‖)是赋范线性空间,且‖x+y‖2+‖x-y‖2=2(‖x‖2+‖y‖2),其中 ‖x‖

(Ⅱ)由 (1),(2)及由定理 2,(X,‖·‖)是赋范线性空间,其中 ‖x‖ =d(x,0)。

又由(3),(X,‖·‖)的范数 ‖x‖满足 ‖x+y‖2+‖x-y‖2=2(‖x‖2+‖y‖2),故由定理 5(Ⅱ)知,在(X,‖·‖)中可定义内积〈x,y〉:

使(X,〈·,·〉)是内积空间,且 d(x,y)=‖x-y‖,‖x‖

于是

定理 7 (Ⅰ)若 (X,〈·,·〉)是内积空间,则 d2(x,y)+d2(x,-y)=2(d2(x,0)+d2(0, y))。其中 d(x,y)

(Ⅱ)若 (X,d)是线性距离空间,且

(1)d(αx,0) =|α|d(x,0);

(2)d(x+z,y+z)=d(x,y);

(3)d2(x,y)+d2(x,-y) =2(d2(x,0)+d2(0,y))。

则(X,〈·,·〉)是内积空间,其中

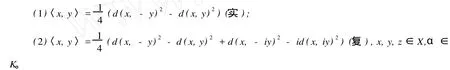
证明:(Ⅰ)同定理 6一样可证

(Ⅱ)由 (1),(2)及定理 3,(X,‖·‖)是赋范线性空间,其中 ‖x‖ =d(x,0)。

又由(3),(X,‖·‖)的范数 ‖x‖满足 ‖x+y‖2+‖x-y‖2=2(‖x‖2+‖y‖2),故由定理 5(Ⅱ)知,在(X,‖·‖)可定义内积〈x,y〉:

于是

定理 8 (Ⅰ)若 (X,〈·,·〉)是内积空间,则 d2(x,y)+d2(x,-y)=2(d2(x,0)+d2(0, y))。其中

(Ⅱ)若 (X,d)是线性距离空间,且

(1)d(αx,0)=|a|d(x,0);

(2)d(x+y,0)≤d(x,0)+d(y,0);

(3)d2(x,y)+d2(x,-y) =2(d2(x,0)+d2(0,y))。

则(X,〈·,·〉)是内积空间,其中

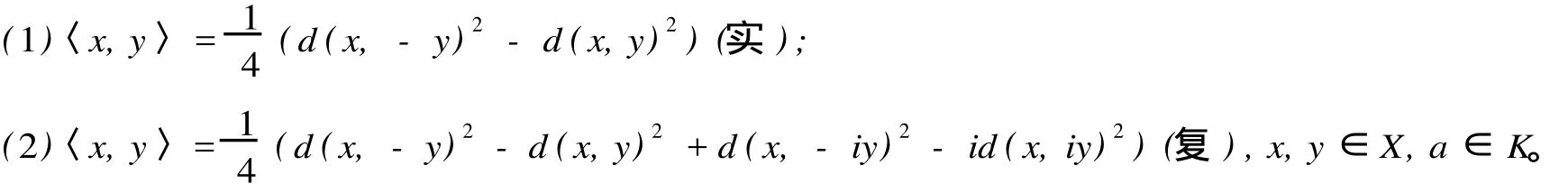
证明:(Ⅰ)同定理 6一样可证。

(Ⅱ)由 (1),(2)及定理4,(X,‖·‖)是赋范线性空间,其中 ‖x‖ =d(x,0)。又由 (3), (X,‖·‖)的范数 ‖x‖满足 ‖x+y‖2+‖x-y‖2=2(‖x‖2+‖y‖2),故由定理5(Ⅱ)知,在(x,‖·‖)可定义内积〈x,y〉:

于是

[1].程其襄等编 .实变函数与泛函分析基础 [M],北京:高等教育出版社 (第二版)[M].2007.

[2].刘培德编著 .泛函分析基础 [M].武汉:武汉大学出版社,2004.

[3].匡继昌编著 .实分析与泛函分析 [M].北京:高国防工业出版社,2002.

(责任编辑 刘洪基)

Sufficient and Necessary Condition for L inear D istance SpaceMake Up Normed L inear Space and Inner Product Space

LANG Ka i-lu
(Department of M athematics,Chuxiong N or m al University,Chuxiong675000,China)

In this paper,the author gives one sufficient and necessary condition for linear distance space make up normed linear space and three sufficient and necessary conditions for linear distance space make up inner product space.

linear distance space;normed llinear space;inner product space;sufficient and necessary condition

O177

A

1671-7406(2010)03-0018-04

2009-11-23

郎开禄 (1962—),男,云南楚雄人,副教授,主要研究方向:高等数学及数学分析。