Banach不动点定理的推广及应用
2010-09-07张超
张 超
(淮南师范学院数学与计算科学系,安徽 淮南 232001)
Banach不动点定理的推广及应用
张 超
(淮南师范学院数学与计算科学系,安徽 淮南 232001)
本文主要讨论完备距离空间中Banach不动点定理,给出了定理的一些推广结果和改进形式,并举例说明了Banach不动点定理在经济上的应用。
压缩映射;Banach不动点定理;完备空间;均衡
1 引言
不动点理论[1]是目前正在迅速发展的非线性泛函分析理论的重要组成部分,它与近代数学的许多分支有着紧密的联系。泛函分析[3,5,6]以其高度的统一性和广泛的应用性在现代数学领域占有重要的地位。微积分中的隐函数存在唯一性定理,代数方程、微分方程和积分方程的求解都可以归结为泛函分析中的Banach不动点定理来求某映射的不动点。Banach不动点定理实际上是算子方程的求解问题,它提供了解的逼近程序和近似解的构造。本文就从其数学本质出发,讨论完备赋范线性空间 Banach不动点定理,给出了定理的一些推广结果和改进形式,并举例说明了Banach不动点定理在经济上的应用。
定义1.1[1]称 T:(X,ρ)→(X,ρ)是一个压缩映射。如果存在0<α<1使得ρ(Tx,Ty)≤α ρ(x,y)(∀x,y∈X)。
定义 1.2[4]设 X是线性空间,E⊂X称 E为一凸集,如果λx+(1-λ)y∈E(∀x,y∈E,∀0≤λ≤1)。
定义 1.3[2]给定一个私有制经济我们说配置和价格向量 P构成一个竞争(或瓦尔拉斯)均衡。如果它们满足下列条件:
(3)市场出清:对于每一种商品
2 主要结果
定理2.1[1](B anach不动点定理)设 (X,d)是完备距离空间,T∶X→X并且对任意x,y∈X,有 d(Tx,Ty)≤θd(x,y),其中 0<θ<1,则存在唯一的∈X使得
现在我们将定理 2.1进行推广,有以下定理:
定理 2.2 设(X,d)是完备的,T是X到自身的映射,且存在 n>1使 Tn=TTT……Τ∶X→X是压缩映射,则 T∶X→X有唯一的不动点 x∈X。
证明:由定理 2.1 有唯一的 x∈X使得 Tnx =x因为 Tn(Tx)=Tn+1x =T(Tnx) =Tx故 Tx也是 Tn的唯一不动点,所以 x =Tx即 x是 T的不动点。若 y =Ty显然y也是 Tn的不动点,由 Tn的不动点的唯一性,知必有 x=y即 T的不动点是唯一的,证毕。
例 设 F∶R→R且 F(x)在R上可导,并且满足 |F′(x)|≤α<1,则由中值定理 |F(x) -F(y)|=|F′(ξ)(x-y)|≤α|x-y|(ξ在 x与 y之间)即 d(F(x),F(y))≤αd(x,y)。0≤α<1,故 F是压缩映射,R完备,从而方程 F(x)=x。必有唯一的实数根 x任取 x0∈R由迭代法:xn=F(xn-1)。n=1,2,……,可得近似解 xn的误差估计
下面我们将巴拿赫不动点定理中的压缩因子α的条件放宽,可得下面定理。
定理 2.3 设(x,d)是完备距离空间,F是X→X的映射,不必连续,但满足以下条件:对任意 ε>0总存在δ>0使得当 d(x,Fx)<δ时 F[B(x,ε)]⊂B(x,ε)这里B(x,ε)表示以x为中心以 ε为半径的实心球,那么当对某 u∈x有 d(Fnu,Fn-1u)→0时。序列{Fnu}收敛于F的不动点。
证明:记 u的 n次迭代 Fnu为 un先证{un}是柯西列。给定 ε>0取N充分大,使当 n≥N时 d(un,un+1)<δ(ε)因 d(un,Fun)<δ按条件成立。F[B(un,ε)]⊂B(uN,ε)因此 FuN=uN+1∈B(uN,ε)用数学归纳法可证对一切 k≥0,Fkun=un+k∈B(un,ε)即 d(un,un+k)<ε对k≥0都成立,这表明{un}是柯西列。
由于 X是完备的,存在 u使 un→u,可证 u是 F的不动点,如若不然,则 d(u,Fu)= α >0我们取使得。仍由条件可知将有另一方面,有。可知这个矛盾说明证毕。
定理 2.4 设(X,d)是完备的距离空间,若 d(Fx,Fy)≤α(x,y)d(x,y)。其中 a∶X×X→R+是二元函数,具有性质:对任何闭区间[a,b](a>0),满足 sup({α(x,y)}/α)≤d(x,y)≤b=λ(a,b)<1则 F有唯一的不动点 u,且 n次迭代值 Fnx→u对任何 x∈X都成立。
证明:对任何 x∈X序列{d(Fnx,Fn+1x)}是不增的,故必收敛于某常数 a≥0。今证 a=0,对充分大的 n,d(Fnx,Fn+1)≤a+1。对这种 n及 c=λ(α,α+1),用归纳法将可得α≤d(Fn+kx,Fn+k+1x)≤ckd(Fnx,Fn+1x)≤ck(α+1),因 0 因此 F[B(x,ε)]⊂B(x,ε),即 F有唯一的不动点,证毕。 命题 3.1 假设 z(p)是定义在 p∈Rn ++上的函数,满足 (1)z(p)是连续的;(2)z(p)是零次齐次的;(3)z(p)P;(4)存在一个 s>0使得 zl(p)≥-s;(5)如果 pm→p,这里 p≠0,存在某个五条性质。那么方程组 z(p)=0一定有解。因此,对于任意的纯交换经济,如果0每个消费者 i的偏好≥,i是连续的、严格凸的和强单调的,那么一定存在一个瓦尔拉斯均衡。 我们记 f(p)⊂△里的元素为 p。 (1)对于任意的我们构造一个不动点对应,对于任意的 p∈△0,我们定义 f(p)=即是给定现行价格 p所有使得超需求向量的值最大的q∈△组成它的一个对应,这个对应f()的经济含义是它相当于一个规则。按照这个规则,现行价格向删除超需求的方向调整,实际上就是把具有最大超需求的商品的价格调整到最高的价格上去。或者我们有 因此,如果 z(p)≠0那么 f(p)⊂∂△ =△-△0这里 ∂△表示 △的边界点的集合。如果 z(p) =0那么 f(p)=△。 (2)对于任意的 p∈∂△我们构造一个不动点对应。对于任意的 p∈∂△我们定义 f(p)=注意到如此构造的对应使得 ∂△上的点不可能是不动点,因此如果 p∈∂△那么 pp>0所以 p f(p)。 (3)f()的一个不动点的一个均衡,假设 p∈f(p)在 (2)里我们已经指出 p ∂△所以 p≫ 0如果 z(p)≠0,由(1)知,f(p)⊂ ∂△ =△-△0不可能有 p∈f(p)。因此如果 p∈f(p),一定有 z(p)=0。 (4)不动点对应 f()是凸集。如果 p∈△0对于任意的 q1,q2∈f(p),λ∈[0,1]由 f(p)的定义,对于任意的 q∈△′有 z(p)qi≥z(p)q′,i=1,2,…从而 z(p)[λq1+(1-λ)q2]≥z(p)q′所以λq1+(1-λ)q2∈f(p)。同样的,如果 p∈∂△对于任意的 q1,q2∈f(p)。λ∈[0,1]。由 f(p)的定义,有 pqi=0,i=1,2…从而 p (λq1+(1-λ)q2)=0所以λq1+(1 -λ)q2∈f(p)。为了证明 f()的上半连续性,考略两个序列 pm→p,qm→q这里 qm∈f(pm)我们需要证明 q∈f(p),分两种情况证明:p∈△0和 p∈∂△。如果 p∈△0,那么对于充分大的m,有 pm≫ 0由于任意的 q′∈△有 z(pm)qm≥z(pm)q′由 z()的连续性,我们有z(p)q≥z(p)q′所以 q∈f(p)如果 p∈∂△,假设 pt>0我们将证明对于充分大的m,有。从而 ql=0因此 q∈f(p),由于 pl>0,存在一个 ε>0使得对于充分大的m有 pml> ε,如果 pm∈∂△由 f(pm)的定义,有=0。如果 pm∈△0命题 3.1的题中条件 (4)和(5)蕴涵,对于充分大的m。我们必定有因此=0为证明上述不等式,注意到由命题 3.1中条件(5),此不等式的右边趋于无穷大,如果左边是负的,上述不等式显然成立,如果它是正的,那么上述不等式仍然成立,这里 s由命题 3.1中条件(4)给出。 (5)由不动点定理告诉我们任意一个从非空凸紧集到自身的凸值,上半连续对应有一个不动点,由于 △是非空凸紧集,f()是一个凸值,上半连续对应,所以存在一个 p∈△满足p∈△由 p∈f(p)。由 (3)可得这个 p就是均衡价格向量。 [1]D.R.斯玛特著,张石生,康世锟,马意海译 .不动点定理 [M].重庆:重庆出版社,1982. [2]张定胜编著 .高级微观经济 .邹恒甫总主编 .现代经济学前沿丛书 [M].武汉:武汉大学出版社,2000. [3]夏道行等编著,实变函数与泛函分析 [M].人民教育出版社,1978. [4]郑维行,王声望编 .实变函数与泛函分析概要 (第二册)[M].北京:人民教育出版社,1980. [5]Walter Rudin.FunctionalAnalysis[M].北京:机械工业出版社,2004. [6]Ruth F C.FunctionalAnalysis inModernAppliedmathematics[M].London:Academ ic Press,2009. (责任编辑:刘洪基) Generalization and Application of Banach Fixed Point Theorem ZHANG Chao In this paper,the author studies Banach fixed point theorem in complete distance space,and gives some extended results and its improved forms,also illustrates its application to economy. contractive mapping;Banach fixed point theorem;complete space;equilibrium O18 A 1671-7406(2010)03-0022-04 2009-11-23 淮南师范学院青年教师科研资助计划 (项目编号:2007Lkq06)。 张 超 (1974—),男,安徽固镇人,硕士,副教授,研究方向:金融数学。3 应用
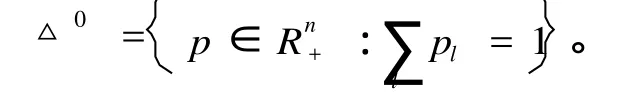
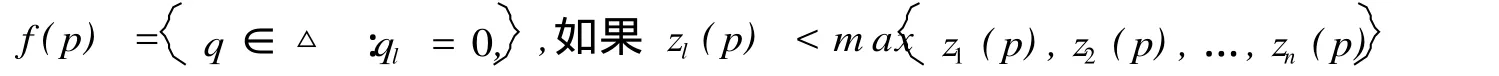
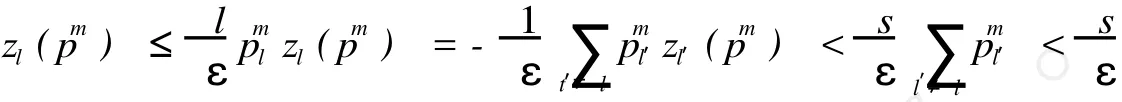
(Departm ent of M athem atics and Computer Science,Huainan N or mal University, Huainan232001,China)
