等负荷钢轨螺纹联接的有限元分析及结构参数优化

苗德华，张纪明，门长峰，杨 强，王艳丽

（1.天津工程师范学院机械工程学院，天津 300222；2.浙江乍浦实业股份有限公司，乍浦 314201）

等负荷钢轨螺纹联接的有限元分析及结构参数优化

苗德华1，张纪明2，门长峰1，杨 强1，王艳丽1

（1.天津工程师范学院机械工程学院，天津 300222；2.浙江乍浦实业股份有限公司，乍浦 314201）

以ANSYS为平台，对等负荷钢轨螺纹联接进行了有限元分析。仿真结果表明:通过轴向切削螺母螺纹牙的方法,可以较好地降低最大轴向应力及有效地改善应力分布不均的现象。同时，提出并验证了如果将螺旋升角进一步增大，改善的效果会更好，即最大轴向应力可降低38.9%以上。

钢轨螺栓；应力分布；等负荷螺母；有限元法；强度

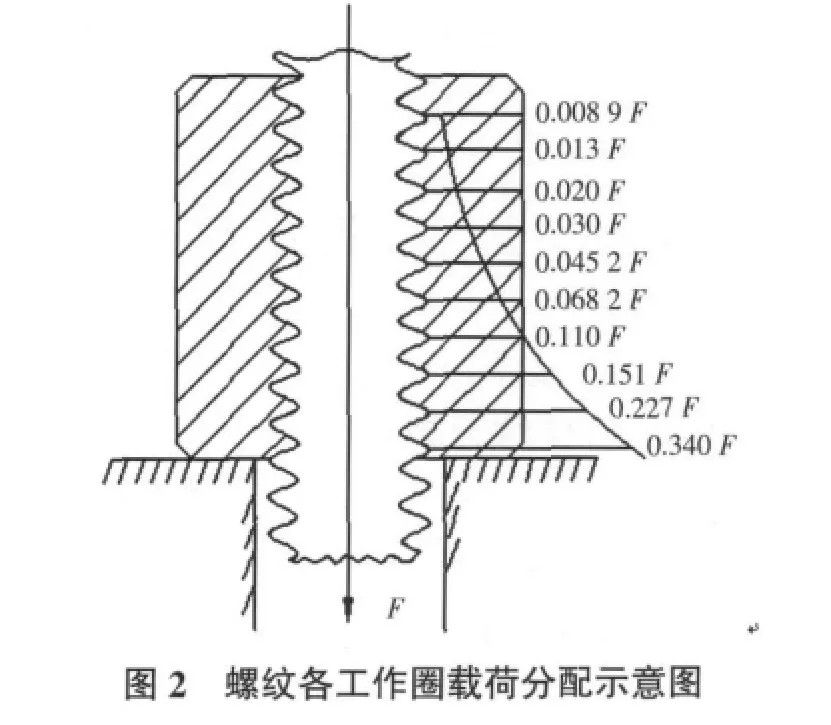
钢轨螺栓是联接钢轨与枕木的关键零件，其强度直接影响钢轨与枕木联接的安全性和可靠性，进而影响机车的安全。在工程实际中螺栓的疲劳断裂大多发生在螺母与被联接件接触面附近的螺纹根部，这是因为螺栓根部应力分布不均匀、应力集中现象严重。在交变载荷的作用下，当其根部应力超过一定数值时将产生局部初始裂纹，随着循环次数的增加其裂纹不断扩展，最终产生疲劳断裂[1]。研究表明，普通螺栓在受轴向力作用时，联接螺纹的各牙受力很不均匀。实验证明，有1/3的载荷集中在第1圈上，第8圈以后的螺纹几乎不受力[2]，最大应力值出现在螺母与被联接件附近的螺纹根部。为了改善这种螺纹牙应力分布严重不均的现象，从而提高螺栓的联接强度，人们进行了不懈的探索，设计出多种新型结构的螺纹联接。孟兆明等人依据山本晃教授[3，4]对螺栓、螺母、螺纹牙受力及其变形的成果，提出了等载荷螺纹，并从螺母螺纹加工难易程度考虑，提出了近似等负荷螺纹。本文利用MATLAB强大的数学运算功能和ANSYS仿真平台，对这种等负荷螺纹进行有限元分析，对螺母螺纹进行结构优化。

1 等负荷螺母的设计

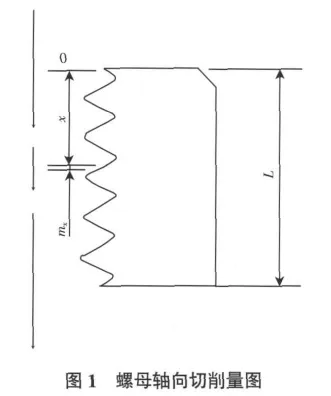
等载荷螺母结构，是在各螺纹牙承受相同载荷的前提下，依据螺栓和螺母的拉压弹性变形关系和内外螺纹的变形协调条件推导得出的[2]，其示意图如图1所示。它是当螺栓螺纹采用标准尺寸时，标准螺母螺纹在x位置单侧面（上面）轴向切削量为mx，其大小与螺母的材料、结构、尺寸及载荷等有关。

由图1可知，随着x的变大，轴向切削量也变大，而且变化速度越来越快。这种变化趋势可以有如下解释：将外载荷从零到最大值逐渐施加到螺母上，当外载荷较小时，远离被连接件处（x较小处）的螺纹首先发生接触，并产生变形，当外载变大时，距离被联接件较近（x较大处）的螺纹陆续发生接触。这样由于x较小处的螺纹首先发生接触就会承受较原普通螺纹更大的力，而x较大处的螺纹受力变小，从而达到降低最大轴向载荷和应力均布的目的。mx增大的越来越快，这与图2所示的各螺纹牙受力严重不均的实际相对应。

2 等负荷螺纹联接的有限元分析

2.1 有限元模型的建立

本文以60 kg·m-1“钢轨铺设的无缝线路上的螺栓连接组合”作为计算模型，采用的轨枕间距为55 cm。所用钢轨螺栓的材料为20 MnTiB，弹性模量为210 GPa，泊松比υ为0.28。螺栓长度为72 mm，螺纹公称直径d0为24 mm，螺纹中径d1为22.051 mm，螺距P为3 mm，螺纹牙形角α为30°，与螺母的旋合长度为27 mm，有限元模型上施加的分布载荷P为1.96 MPa。

为了保证螺纹联接有足够的静强度和锁紧能力，在x=0处螺纹牙的轴向切削量为0。本文采用特征建模的方法，抓住反映物理模型的本质特征，对其做出准确、合理的简化。首先螺旋升角很小，为了减少计算量，将其视为轴对称模型，将六角形螺母简化为等横截面积的圆形螺母，忽略螺帽和部分倒角的影响。而将螺纹联接部分严格按照ISO标准螺纹牙建模。其有限元模型如图3所示。图中水平向左为Y轴正向，竖直向上为X轴正向。

2.2 单元划分

有限元模型的单元划分不但影响计算速度，而且影响计算精度。因此，单元划分是有限元分析的关键点之一。单元划分应疏密合理，符合应力分布规律。在应力变化梯度较大的螺纹处，为了较好地反映应力变化情况，需要采用比较密集的网格，而在应力变化梯度较小的部位，则应划分相对稀疏的网格[5]。模型单元划分网格图如图4所示。

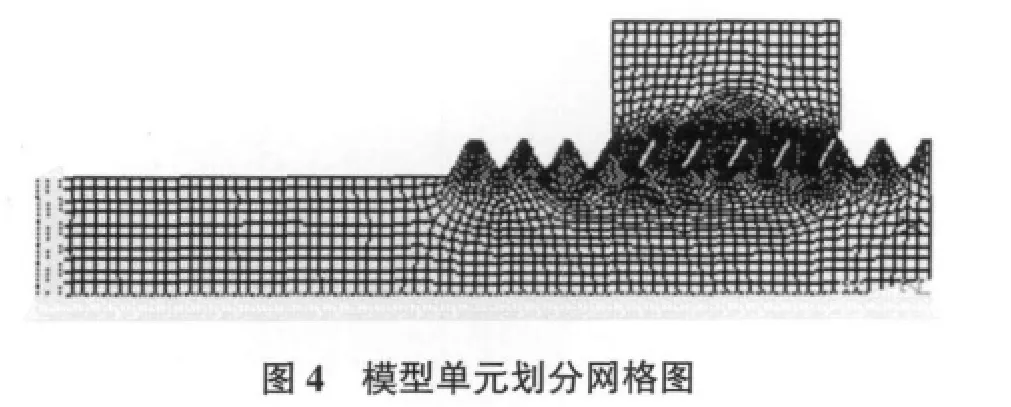
针对所建模型而言，在螺纹根部应力集中的地方，网格应该足够密，螺栓和螺母之间按接触分析处理，其中接触对的建立是能否正确求解的关键。本文目标面选用 TARGE172单元，接触单元选用CONTA169单元，它们是覆盖在有中节点的2-D实体单元表面。建立接触对时，应根据实际情况合理设置单元关键字和实常数。由于将螺母螺纹牙轴向切削后，接触面和目标面将产生空隙，应当按多载荷步进行加载。第一个载荷步施加位移约束，使目标面和接触面之间产生接触；第二个载荷步用分布载荷代替被联接件对螺母的作用。

2.3 仿真结果分析

按照螺母螺纹轴向切削量mx的求解公式[3]，即

其中:

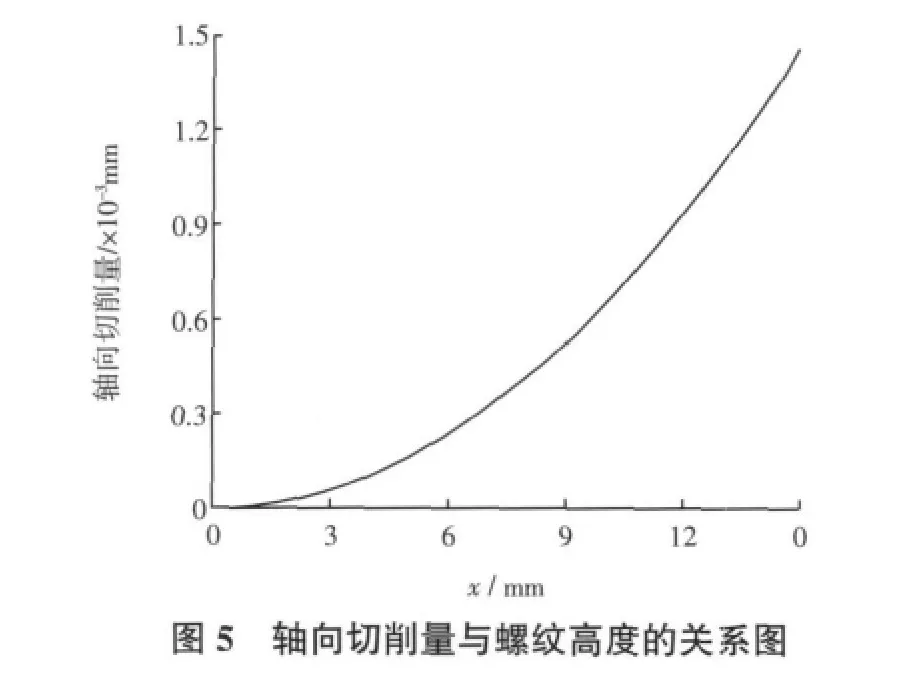
经过MATLAB数学运算[6]，得到轴向切削量mx随x变化的曲线如图5所示。

经ANSYS仿真后，普通螺纹与改进后螺纹轴向应力分布图如图6所示。由图6可知，最大轴向应力均发生在靠近被联接件的第一扣螺纹根部，但其大小却减小很多，以后各牙受力逐渐减小，这与实际情况相吻合。

由于钢轨螺栓的断裂一般发生在螺母与钢轨接触面附近，为此应用图3所示的有限元模型，取每一个螺纹牙平均切削量作为二维模型的轴向切削量进行仿真，对螺母与钢轨接触面附近的螺栓根部的最大轴向拉应力进行分析，其计算结果如表1所示。

表1 普通螺纹与改进后螺纹轴向应力分布

由表1可知，最大轴向应力均发生在靠近被联接件的第一扣螺纹根部，但等负荷螺纹联接相对普通螺纹联接其轴向应力大小却减小很多，同时各牙螺纹根部轴向应力分布有很好的改善，等负荷螺纹联接中第一扣螺纹根部轴向应力有所下降，且各个螺纹牙根部的应力分布得到较大改善，但距离较理想的结果即应力分布相对均匀状况还相差甚远。

3 等负荷螺纹联接结构参数的优化

3.1 近似等负荷螺纹的设计及应力分析

由图1可知，螺纹牙越靠近被联接件其轴向切削量越大，且变化速度越来越快。由于螺母螺纹轴向切削量mx公式复杂，准确加工是非常不现实的，因此提出了近似等负荷螺纹的轴向切削量变化公式[3]，即将螺母的受力单侧面按等螺旋升角λ*将原标准螺纹切削一次，公式为：

其中：L为旋合长度；n为螺纹旋合圈数；dp为螺纹中径；mx为高度为L时的螺纹轴向切削量。

同样，利用ANSYS软件，按照上述给定的λ*进行仿真分析，其几何模型的轴向切削量均用相应螺距内的平均切削量来代替。有限元模型局部放大图如图7所示，仿真分析结果如表2所示。

3.2 近似等负荷螺纹螺旋升角的优化

通过与普通螺纹联接时螺纹牙根部的应力进行对比可知，这种方法可以大幅度降低最大轴向应力值，其中最大降幅在10.49%左右，并且各个螺纹牙的载荷分布也得到了较好的均化。但是距理想中的等负荷状况还有较大差距，根据轴向切削量与应力变化的关系及上述MATLAB与ANSYS仿真分析结果可知：与普通螺纹联接相比，优化后的螺纹联接中，随着轴向切削量的增大，仿真分析所得各螺纹牙根部最大轴向应力的改善情况是有规律可循的，即随着轴向切削量的增大，各个螺纹牙根部的应力分布得到较大改善，且距离较理想的结果即应力分布相对均匀，应力集中现象很小相差不远。为此，采用适当调节螺旋升角的大小，将螺纹高度为L处的螺纹轴向切削量增大至mmax=0.002 mm后，同样利用仿真软件进行分析，所得结果如表3所示。

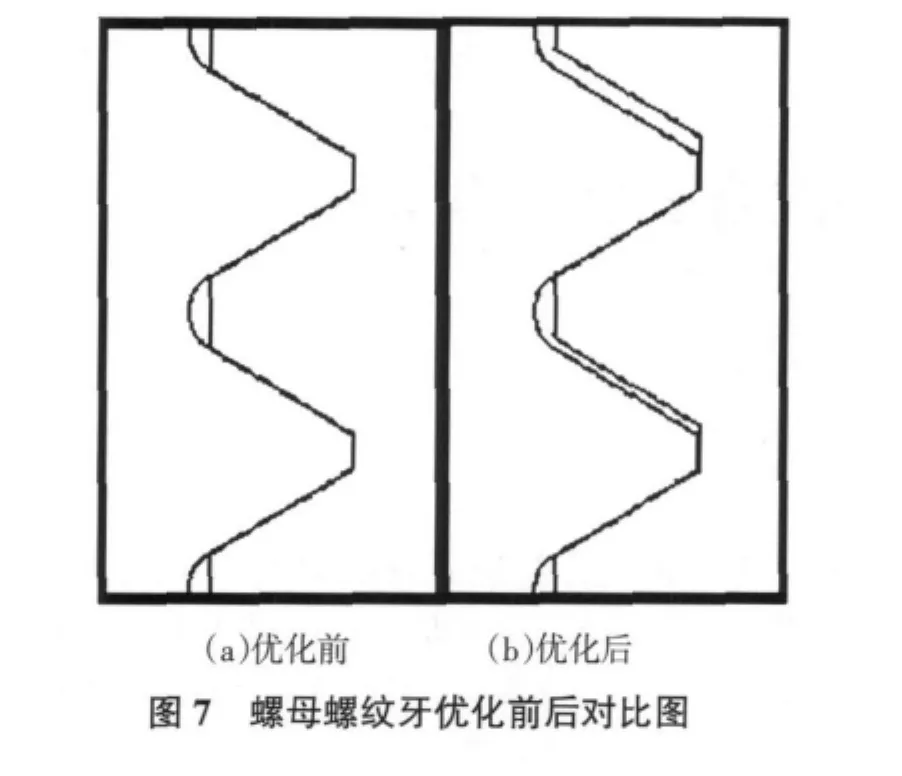
表2 螺栓各螺纹牙根部的最大轴向应力

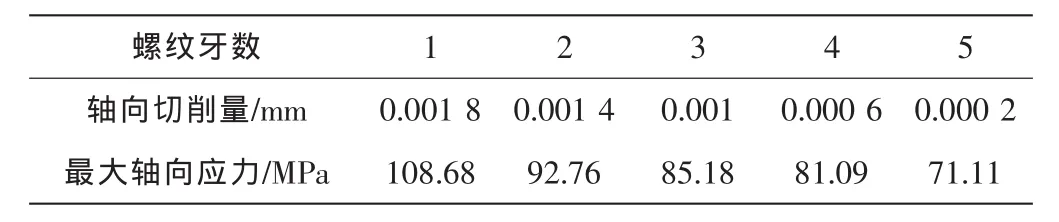
表3 螺栓各螺纹牙根部的最大轴向应力

由以上数据可知，此时的轴向应力分布得到进一步改善，继续将螺纹高度为L处的螺纹轴向切削量增大至mx=0.003 mm进行分析，螺栓各螺纹牙根部的最大轴向应力如表4所示。

由表4可见，此时的轴向应力分布得到较好的改善，各个螺纹牙所承受的轴向载荷趋于一致。由此可以推得：只要通过适当增大螺纹升角，完全可以实现螺纹的近似等载荷。

以上各种情况下改善轴向应力的效果可以通过图8直观地表现出来。

表4 螺栓各螺纹牙根部的最大轴向应力

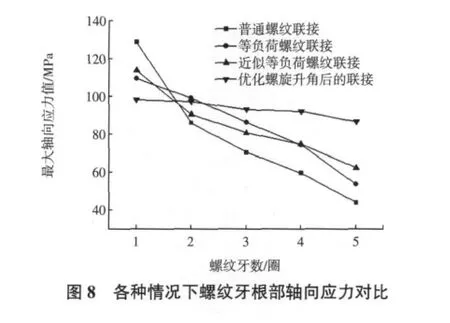
由图8可知，虽然在理论推导和仿真建模中用了较多的假设和简化，例如将螺纹梯形截面的变形作为平面问题处理，在建模时将三维模型简化为二维轴对称模型等，这些都必然会产生一定的误差，但相比普通螺纹联接而言，等负荷螺纹联接及对其优化后的螺纹联接仍不失为一种提高螺纹承载能力的好方法，对切削量大小的判定具有指导意义，而最佳的轴向切削量应该通过实验来决定和验证。

4 结论

（1）根据山本晃教授的理论所推倒出来的用于改善螺纹牙受力不均现象的公式是可取的，仿真结果表明，它可以明显降低最大螺纹牙根部的受力情况，同时改善螺纹牙受力不均的现象。

（2）等负荷螺纹可以大大提高螺纹联接强度，但对螺纹加工的精度要求较高，加工较难。

（3）近似等负荷螺纹不仅能较好地改善螺纹牙受力不均等现象，且加工容易。当优化螺旋升角后，即将螺纹高度为L处的螺纹轴向切削量增大至mx=0.003 mm时，各螺纹牙的轴向应力分布趋于一致，且最大轴向应力可降低38.9%以上。

（4）虽然在理论推导和仿真建模中用了较多的假设和简化，使得理论值与实际值之间有一定的差距，但是等负荷螺纹联接仍不失为一种提高螺纹承载能力的好方法，对切削量大小的判定具有指导意义，而最佳的轴向切削量应该通过实验来决定和验证。

参考文献：

［1］ 苗德华，薛强.提高钢轨螺栓疲劳强度的有效方法[J]．铁道建筑，2005（2）:33-35.

［2］ 濮良贵，纪名刚.机械设计 [M].北京：高等教育出版社，2001．

［3］ 孟兆明，闫德元，郭可谦．一种提高螺栓联接强度的新方法[J]．北京航空航天大学学报，1995，21（3）：109-102.

［4］ 山本晃.螺纹联接的理论与计算[M].郭可谦,译.上海：上海科学技术出版社，1984.

［5］ 刘涛，杨凤鹏.精通ANSYS[M].北京：清华大学出版社，2002：97-106.

［6］ 王沫然．MATLAB与科学计算[M].2版.北京：电子工业出版社，2003.

FEA and optimization of structure parameters on rail bolt connection of equal load

MIAO De-hua1，ZHANG Ji-ming2，MEN Chang-feng1，YANG Qiang1，WANG Yan-li1
（1.School of Mechanical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China；2.Zhejiang Zhapu Industrial Co.Ltd.，Zhapu 314201，China）

A finite element analysis to the thread connecting of equal load is made by using ANSYS as platform.The results show that the maximum axial stress can be reduced and the stress distribution phenomenon also can be improved by using the method of axial cutting the teeth of the nut thread.In the meantime，an approach of reducing maximal axial stress is given,which increasing the helix lead angle furthmore.It shows that this method can reduce maximal axial stress by more than 38.9%.

rail bolt；stress distribution；nut of equal load；finite element；strength

book=2,ebook=62

U213.5

A

1673－1018（2010）02－0001－04

2010-04-23

人力资源和社会保障部科技项目（LS200506）.

苗德华（1957—），男，教授，博士，博士生导师，研究方向为机械强度以及材料疲劳特性等.