一种基于旋转不变技术信号参数估计的改进算法
2010-08-30许博雅郑宏兴
许博雅, 郑宏兴
(天津工程师范学院天线与微波技术研究所,天津 300222)
一种基于旋转不变技术信号参数估计的改进算法
许博雅, 郑宏兴
(天津工程师范学院天线与微波技术研究所,天津 300222)
为了有效估计智能天线系统中来自相关信号源的信号到达方向,提出了一种共轭倒序向量平均的算法,该方法是对二维旋转不变技术的信号参数估计算法的改进。数值实验结果表明,改进算法在不增加计算机资源占用的基础上,既能估计独立信号源的信号到达方向,也能有效地估计相关信号源的信号到达方向。
智能天线;双线性正交线阵;相关信号源;信号到达方向
近年来,移动通信的快速发展对宽带天线的要求越来越高,特别是智能天线的应用日益普及。在这些智能天线系统中,用阵列信号处理方法实现信号到达方向(direction of arrival,DOA)的估计,从而实现自适应波束形成。利用二维DOA估计能够更有效地开发信道的冗余,实现更为精确的定位。因此,二维DOA估计越来越受到人们的重视,提出了诸如基于高阶累积量的多重信号分类算法[1]、二维谱峰搜索方法[2]和基于旋转不变技术的信号参数估计(estimating signal parameters via the rotational invariance technique,ESPRIT)方法[3]等。这些算法能够准确地估计独立信号源的二维DOA,但是,对相关信号源的估计能力较弱。文献[4]给出了一种基于空间平滑技术[5]的改进算法,这种算法能够处理相关信号源,但是没有推广到二维的情形。在双线性正交线阵的二维ESPRIT方法[6]基础上,本文提出了一种共轭倒序[7]向量平均的方法,该方法能够准确地估计独立信号源的二维DOA,在不明显增加计算量的基础上,还能有效地估计相关信号源的DOA。
1 阵列结构及信号模型
如图1所示的双线性正交均匀线阵,该线阵由3个阵元数均为M的子阵列X、Y和Z组成,分别位于正交坐标系x、y和z轴上,各子阵列阵元间距均为d。假设有P个窄带远场平面波入射到阵列,第i个入射波和x、y轴的夹角分别为αi和βi(分别称为方位角和俯仰角),与z轴的夹角为γi,i=1,2,3,…,p,噪声为时
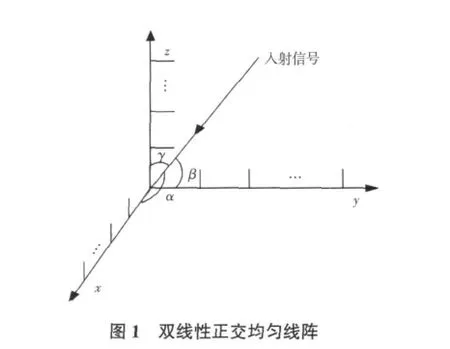
域和空域上统计独立于各信号源的高斯白噪声,则子阵列X、Y和Z的接收数据分别为:

其中:F=X,Y,Z;AF为子阵列的方向矩阵,且

ψ=α,β,γ,且

S(t)=[S1(t)S2(t)… Sp(t)]为入射信号矢量;NF(t)为接收的噪声矢量。由于子阵列X、Y和Z的接收数据都与空间一维角度估计的数学模型相同,可以分别进行一维处理。
2 算法分析
2.1 二维ESPRIT方法
采用图1所示的双线性正交均匀线阵,阵列结构和信号模型如前所述,对x轴阵元的接收数据进行基本ESPRIT算法[6]处理,通过谱峰搜索,便可求出x轴的信号到达角α,同样的对y轴、z轴的接收数据运用ESPRIT算法计算,可得信号空间到达角β和γ。令:
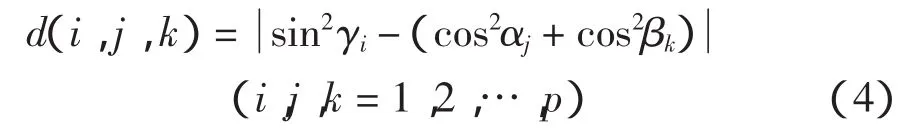
当d(i,j,k)之值充分小时,可以认为(αj,βk)为正确的参量对组合。
2.2 二维ESPRIT改进算法
采用图1所示的双线性正交均匀线阵,阵列结构和信号模型如前所述,考虑子阵列X,计算其接收数据的协方差矩阵R1,对X轴接收数据进行共轭倒序处理,得到:

X*为X的复共轭;JM是M阶交换矩阵,除副对角线上元素为1外,其余元素均为零。
计算X2的协方差矩阵R2,对R1和R2取平均,得:

对R进行特征分解,得到所有大特征值所对应的特征向量所构成的信号子空间U,取U的前N-1行构成矩阵U1,再取后N-1行构成矩阵U2,由于阵列的方向矩阵AX和U所构成的子空间是相等的,所以存在一个唯一的非奇异矩阵T,使U=AXT,于是

其中:AX1是由AX的前N-1行所构成的矩阵;ΦX为旋转矩阵,且ΦX=diag[ejr1,ejr2,…,ejrP];ri=(2πd/λ)cos(αi)。于是

根据总体最小二乘准则(TLS),ESPRIT算法通过解下面的最小问题来获得H的最小二乘解。
构造矩阵U12=[U1U2],实际上就是要寻找一个矩阵F,使其与U12正交,且满足FHF=I,显然,F可从UH
12U12的特征分解中得到。因为

式中:Λ0是由特征值构成的对角矩阵;E是与其相应的特征矢量构成的矩阵,将E分解为四个P×P子矩阵,即

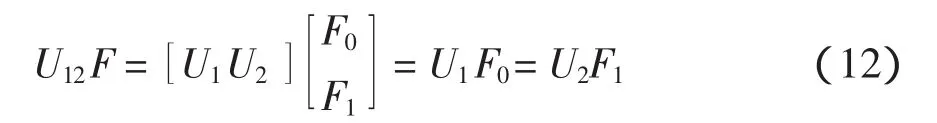
可得


上式说H的特征值就是ΦX中的对角线元素,对其进行特征分解,求出其特征值φi,i=1,2,…,P,用φi来估计方位角αi。
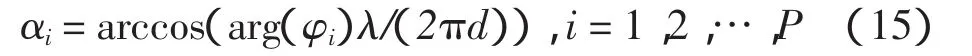
采用同样的方法可以得到βi和γi(i=1,2,…,P)。
由上述步骤可以看出,改进算法对接受数据向量X做共轭倒序后与原数据向量平均,具有平滑的意义,因此,改进算法在不明显增加计算量的基础上,可以对相关信号源进行估计,同时不会影响对非相关信号源的DOA估计性能。文献[7]中指出,采用共轭倒序处理后,可使信源间的相关系数降低为原来的63%。
3 仿真实验
为检验改进算法的性能,将改进算法与原算法作比较,做了如下仿真实验。
例1 各子阵列的阵元数M=8,阵元间距d=λ/ 2,假设有3个相关信号入射到阵列,入射方向分别为(30°,40°)、(60°,55°)和(75°,65°),快拍数为600,信噪比(SNR)为10 dB,做100次Monte Carlo试验。图2和图3分别为采用改进算法和原算法得到的星座图。从图中可以看出,改进算法估计信号方向更为准确,有更好的收敛性。
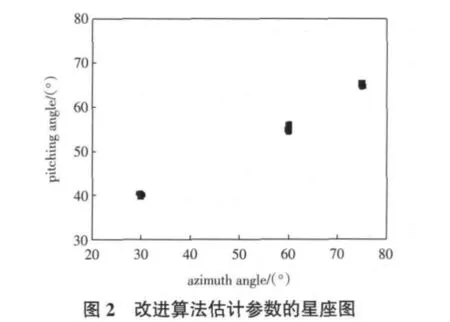
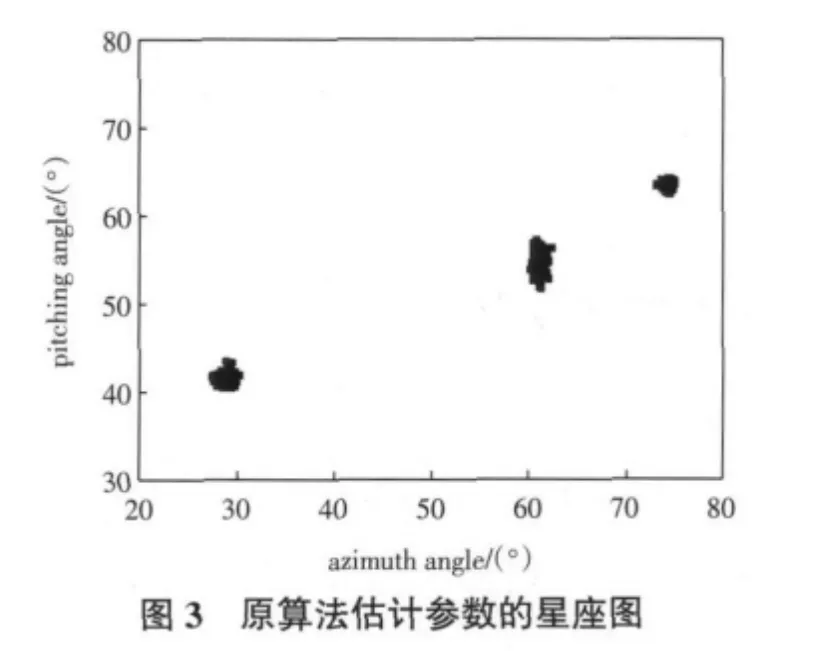
例2 假设有2个相关信号入射到阵列,入射方向分别为(35°,50°)和(60°,85°)。其他条件与例1相同。定义均方根误差为 RMSE=,改变信噪比,得到图4所示的参数估计的RMSE随SNR变化曲线。
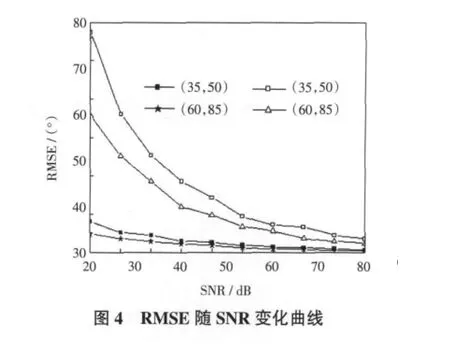
从上面仿真实验结果可以看出,改进算法较之原算法,在同样条件下,误差更小,更能正确的分辨两相邻的相关信号源,即前者对相关信号源的估计性能优于后者,在小信噪比情况下,这种改善尤为明显。
4 结论
本文针对一种特定阵列结构的二维ESPRIT算法进行了改进,改进算法比原算法有更高的分辨力,能有效地分辨出相关信号DOA。该改进算法不仅使二维ESPRIT算法的估计性能更加完善,而且具有一定的应用价值。
[1] 姚敏立,金梁,殷勤业.基于累计量的空间特征估计算法及其在智能天线中的应用[J].信号处理,2000,16(1):58-62.
[2] 战国龙,胡国平.一种新的二维MUSIC算法的研究[J].通信学报,2004,25(4):69-74.
[3] 刘全,王雪松,皇甫堪.二维虚拟ESPRIT算法[J].国防科技大学学报,1999,21(4):63-66.
[4] 郑宏兴,何伟.一种估计相关信号波达方向的改进算法[J].天津工程师范学院学报,2008,18(4):6-9.
[5] SHAN T J,WAX M,KAILATH T.On spatial smoothing for direction-of-arrival estimation of coherent signals[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1985,33(4):806-811.
[6] 战金龙,王安义,卢建军.一种新的二维ESPRIT算法的研究[J].西安电子科技大学学报,2003,30(4):561-564.
[7] 何子述,黄振兴,向敬成.修正MUSIC算法对相关信号源的DOA估计性能[J].通信学报,2000,21(10):14-17.
A modified algorithm based on estimating signal parameters via rotational invariance technique
XU Bo-ya,ZHENG Hong-xing
(Institute of Antenna and Microwave Techniques,Tianjin University of Technology and Education,Tianjin 300222,China)
In order to estimate the signal direction of arrival from correlated signal sources in smart antenna system,an algorithm is proposed,which is named conjectured vector of inversed order.The algorithm is from modified two-dimensional estimating signal parameters via the rotational invariance technique.Numerical experiment shows that the proposed algorithm can estimate the signal direction of arrival from independent signal sources efficiently.Furthermore,it can estimate the signal direction of arrival from correlated signal sources without additional computer resources obviously.
smart antenna;bilinear orthogonal linear array;correlated signal source;signal direction of arrival
book=2,ebook=87
O451;TN911
A
1673-1018(2010)02-0020-03
2010-03-01
国家自然科学基金资助项目(60871026);天津工程师范学院青年教师基金资助项目(05010).
许博雅(1983—),男,硕士研究生;郑宏兴(1962—),男,教授,工学博士,硕士生导师,研究方向为电磁场与微波技术.
