SVM的参数优化及在耐热酶和常温酶分类中的应用
2010-08-27张正阳须文波丁彦蕊
张正阳, 须文波, 丁彦蕊
(江南大学信息工程学院,江苏无锡 214122)
SVM的参数优化及在耐热酶和常温酶分类中的应用
张正阳, 须文波*, 丁彦蕊
(江南大学信息工程学院,江苏无锡 214122)
氨基酸的组成是影响蛋白质耐热性的主要因素之一,所以以20种氨基酸所占比例作为特征向量,利用支持向量机(Support vector machine,SVM)预测蛋白质的耐热性。在比较了几何方法、SVM-KNN和重复训练3种参数优化的方法之后,从中选择了几何方法来优化SVM分类器的参数,并使预测率从85.4%提高到88.2%。从预测率上可知:(1)几何方法优化SVM参数可以有效地提高预测率;(2)氨基酸含量与酶的耐热性之间存在极强的相关性。
支持向量机;氨基酸含量;分类;参数优化
耐热酶之所以较常温酶受到更多的关注,是因为它在高温下比常温酶有更多的功能,而且具有反应速度快、不易被杂菌污染等特点,不过它的难以培养、不易获得恐怕是引起更多人兴趣的原因。目前,它主要通过筛选耐热微生物获得,不过产酶量很低。尽管如此,耐热酶仍然在食品酿造、医药、环境保护和金属冶炼等领域得到了广泛的应用。所以本文的出发点就是想通过蛋白质序列信息来研究耐热酶耐热的分子机制,了解蛋白质的折叠过程[1],寻求通过蛋白质工程手段提高常温酶耐热性的途径。
1 研究背景
耐热酶和常温酶都是由20种相同的氨基酸组成,却在高温下表现出截然不同的性质,这的确使人难以理解。而在以往的研究中,人们更多的是从分子生物学、结构生物学的角度,去分析二级结构和三级结构等不同结构层次,来了解某个或某些酶的耐热性。至于研究发现的影响耐热的因素也很多,比如氨基酸组成、二肽含量、氢键、盐桥等。
利用机器学习的方法来研究蛋白质的耐热性近来也受到重视,比如Cheng等人利用序列和结构的信息来预测单个氨基酸突变对耐热性的影响,而他们选择了SVM来进行预测的工作并得到了84%的准确率[2]。而Zhang等人利用新型分类器LogitBoost通过蛋白质主要结构来区分喜温和嗜热的蛋白质,同样也得到了相当好的效果[3]。
本次仿真选用的SVM是由Vapnik和他的合作者一同提出的学习算法[4]。其特点是它不但可以学习复杂的非线性的输入数据,而且还具有足够的健壮性可以避免陷入局部最优的尴尬境地。而这些是发现影响蛋白质耐热性因素所必须具备的条件[2]。它的主要原理是利用核函数把原始数据映射到高维空间,这样可以使得数据有可能变成线性可分的(图1)。其主要特点是不显式地将原始数据映射到高维空间,而是利用核函数K(x,z)=<ø(x)·ø(z)>去隐式计算点乘,从而减少计算的复杂性,这里x,z是原始数据,φ是从输入空间到高维空间的映射[5]。而最终的决策边界即判断每个样本属于哪一类是用
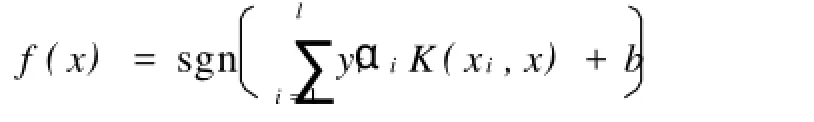
来判断的,其中的K只是起到度量样本x和xi的相似程度的作用,而αi则是在解决QP问题后得到的拉格朗日乘子,而那些支持向量(SVs)对应着不为0的αi[2,5,6]。
目前SVM在解决高维模式识别问题中表现出许多特有的优势,同时它也被广泛用于其他机器学习的问题中比如文本分类、图像识别、手写数字识别和生物信息学等[5]。但是在SVM的应用中还存在着一些问题:(1)核函数的选择和参数的优化。(2)虽然开发了较多算法[6]去解决训练数据过多时,训练时间较长的问题,但是仍有提高的空间。(3)复杂问题分类依旧不是很准确。
本文主要解决的是针对具体问题的SVM参数的优化。这样做最直观的效果是提高了SVM对具
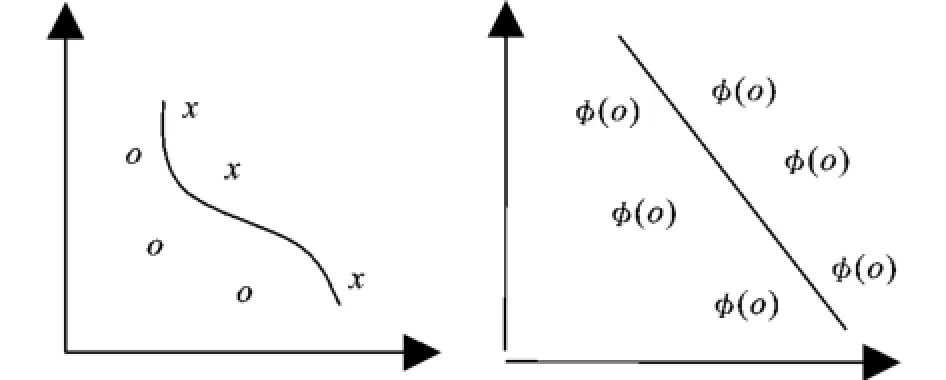
图1 SVM原理Fig.1 SVM principle
体问题的预测率,增加了它的适应性,更重要的是为我们增进对具体问题的认识提供了另一条有效的途径,同时也拓宽了SVM的应用领域。至于目前针对SVM参数优化的方法主要有3种:(1)根据具体问题选用、构造或调整核函数。(2)SVM和其他分类方法相结合。(3)采用新的算法解决QP问题。
接下来,本文将主要介绍SVM训练集的构建,以及3种参数优化的方法。之后,比较和分析预测结果,找出最适合分类耐热酶和常温酶的参数优化方法。
2 方法
2.1 数据集的构建
首先,先从DSMZ[7]数据库中挑选生长温度大于60℃的微生物,并从Swiss-Prot数据库中下载这些微生物的蛋白质序列,同时下载与耐热蛋白质数量相当的常温蛋白质序列,然后去除含有假定、可能、假设等词的蛋白质序列。由于本次仿真是把氨基酸含量当作SVM的特征向量,所以前期还要处理数据,得到20个氨基酸在每个样本里的含量,以此完成数据集的构建。
2.2 参数优化的方法介绍
2.2.1 几何方法 该方法的第一步与通常的SVM训练一样,首先用合适的核函数训练以找出分类面的大体位置,而后放大边界周围的黎曼度量,这主要是通过对核函数的缩放来完成。在这个过程中核心就是对核函数的缩放,其中对之前算法的改进就是使用对边界的直接度量来扩大核函数,而不是先前使用支持向量的方法。具体方法是在第一次训练结束之后,先后使用公式:
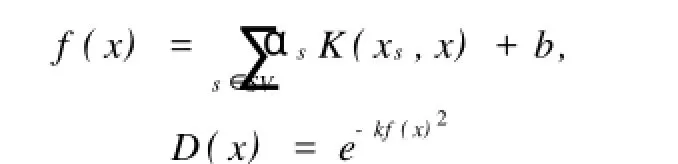
得到f(x),D(x)的值,而后通过下列公式得到调整后的核函数:k(x,x′D(x)K(x,x′)D(x′),然后重复上述过程直至得到最好的预测结果[8,9,10]。
2.2.2 SVM-KNN 由于SVM是可以等同于每类只有一个支持向量为代表点的最近邻分类器(Near Neighbor)的,所以这使得在同一分类问题里使用不同分类器成为可能[11]。而第二种方法就是通过控制分类阈值ε的大小来达到分类的目的。当样本到分类面的距离大于给定的阈值,说明样本离分类面较远,用SVM分类会达到比较好的效果。反之,当距离小于给定的阈值时,用KNN去分类,去计算样本和每个支持向量作为代表点的距离来判断样本所属类别。当然在用KNN分类时,因为计算距离是在特征空间里进行的,所以距离公式要采用如下形式:至于ε的取值一般在0到1之间[11,12]。
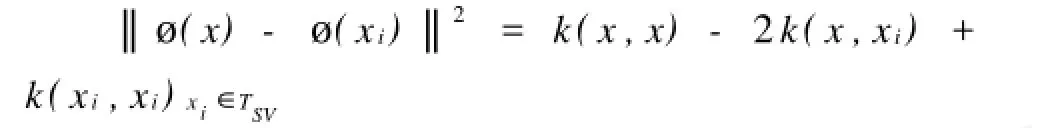
2.2.3 重复训练 该算法的灵感来源于自然界的再学习,即不断地从错误中学习。其出发点就是处理预测结束后测试集中被误分的样例,恰巧这部分通常都是被人遗忘的。而它的核心思想就是将误分的样例加入到原训练集中,以增加支持向量的数量,形成新的分类面,从而提高SVM的预测率。其主要步骤就是先用准备好的训练集测试集训练和预测。而后在得到的结果里,对照测试集挑出被误分的样例并把它们加入到原训练集里。最后,在使用新训练集和原测试集的情况下,得到新的预测率。当然,如果分类效果不好,可以重复上述步骤,
直到得到满意的结果[13]。不过需要注意的是新测试集和原测试集必须是采用同样的方法从相同的数据源得到。
3 仿真结果及分析
在使用陆振波的MATLAB下SVM[14]训练和测试数据时,使用了多个核函数以观察其实际效果,比如线性、多项式、sigmoid和RBF。最终发现RBF(exp-γ‖xi-xj‖2,γ>0)具有较好的性能。不过无论是SVM本身还是核函数RBF都需要调整参数以得到较好的泛化性能和尽量避免过拟合现象的出现。显而易见,此过程中需要调整的参数是RBF中的γ和SVM中C。γ是控制高斯函数最大值的,一旦它增大就会导致一连串的变化,不光提高了高斯函数最大值的上限,也会使得决策边界更加复杂更加不平滑。而C则是αi所能取到的最大值,同时它也控制着训练错误和f(x)平滑度两者之间的平衡。这样导致的后果就是C越大就越会得到高拟合度即低错误率高复杂度的f(x)(决策边界),当然这必须付出过拟合数据的代价[2],而这些都不是我们所希望的,因为我们不想得到只对某一个或几个数据集能有效分类的分类器。所以在仿真开始阶段,主要工作放在替SVM找出合适的参数γ和C来,而结果是当γ=1,C=200时,分类的效果最好为85.4%。而后在Matlab下实现上述三种方法,并使用之前找到的较好参数去预测以期得到良好的分类效果。
第一种方法中需要预设的参数是Κ,仿真时参考了[8]所建议的参数,具体情况见表1。从表中可以明显发现经过该方法优化过的SVM较原始版本预测率上有了提高,至少能维持在原始水平。其中提升最大的是当Κ=0.90×10-3,D=1.92×10-3时,准确率为88.2%比原先的85.4%提高了2.8%。而在多数分组中达到最大准确率的都是各分组的第一组参数,而函数D的值总是在该组中的比较小和比较大的值之间来回地变动,相对应的是每当D在较大值时,准确率至少维持在未优化前的水平即85.4%,而当D在较小值时,准确率一般能达到较高的水平,有的甚至达到了该组的最大值。
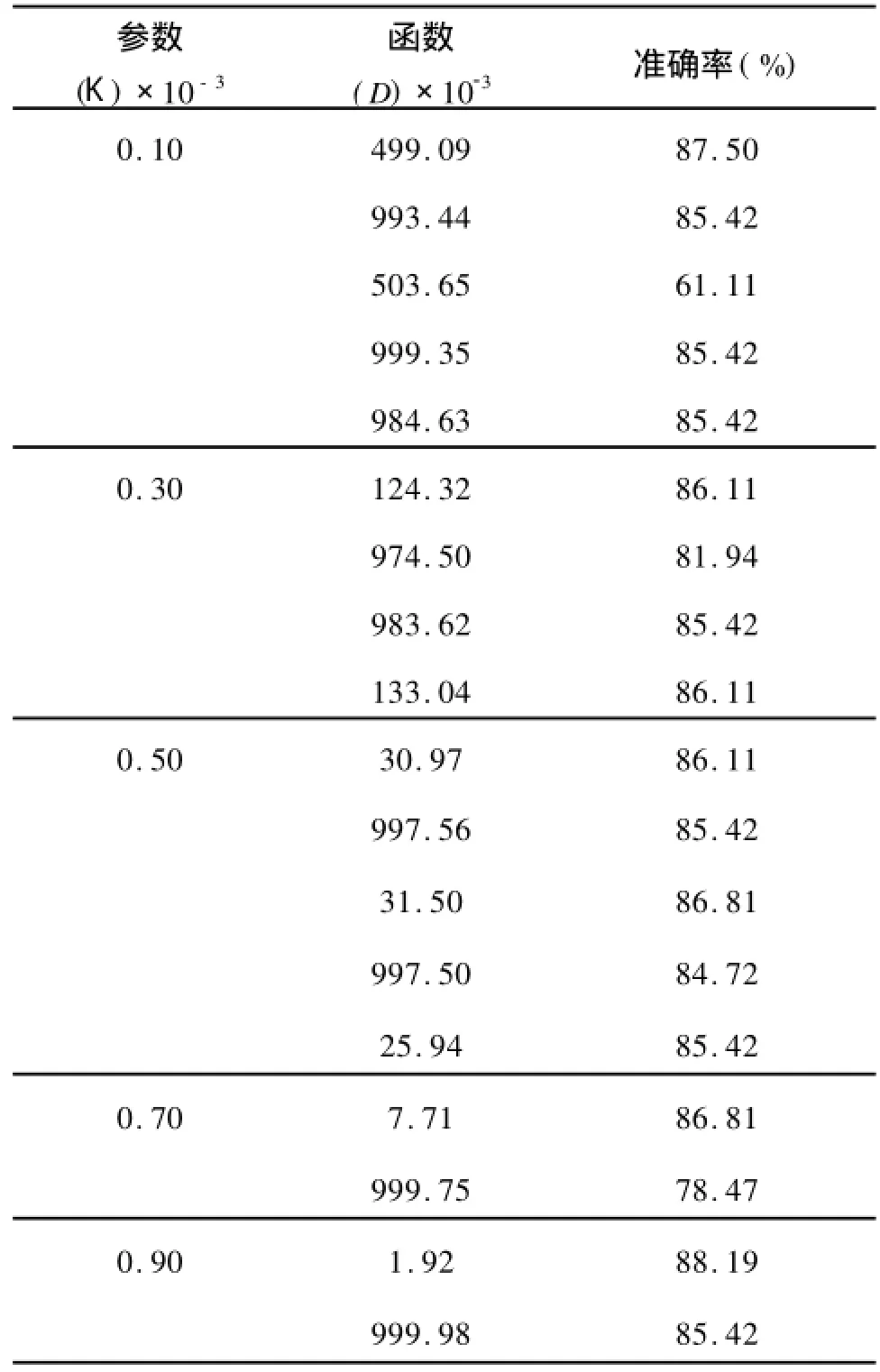
表1 几何方法Tab.1 G eometric method

表2 SVM-KNNTab.2 SVM-KNN

表3 重复训练Tab.3 Repetition training
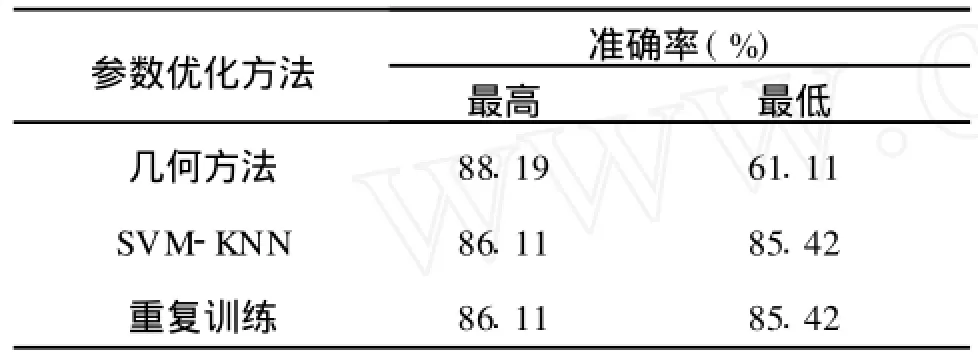
表4 3种方法的比较Tab.4 The comparison of the three methods
第2种方法中需要预设的参数是分类阈值ε,仿真时参考了[11][12]所建议的参数,具体情况见表2。从表中可以看出在ε<0.8之后所有的预测率都跟原始的一样。这说明了KNN发挥作用也只是限于ε在0.8-1之间,所提升的空间为0.7%,这点可以让我们知道在特征空间里此仿真样例到分类面的最小距离都比0.7要大,所以才会导致一旦ε<0.8时,该分类算法采用SVM来分类,而不是KNN,继而得出的预测结果与使用原始方法得到的结果一致。
第3种方法需要说明的是在对照测试集后,本仿真共得到50个错分的样例,在加入到原训练集之后与原测试集一起完成仿真,仿真结果见表3。从表中可以看出,相对于原SVM,新SVM在支持向量个数上增加了57个,占原支持向量个数的51.4%,而预测率提高了0.7%。这一切都符合了该算法的思想,即在新训练集是由原训练集和错分样例构成的情况下,重新训练SVM以获得更多的支持向量并形成新的分类面,从而达到提高预测率的目的。
而针对这3种方法的比较见表4,从表中可以明显地看出,几何方法的最低准确率只有61.1%,但是考虑到该方法是反复调整参数,因此总能取到最大的准确率,而且在表1中该方法大多数的准确率都维持在85.4%左右,所以不必担心其分类能力。而在最高准确率分组中,几何方法以88.2%的准确率位居榜首。而其他两种方法无论是在最高或最低准确率上都保持一致。
4 结 语
本文使用了3种参数优化的方法来提高SVM在分类耐热酶和常温酶过程中的预测率并且都取得了比较好的分类效果,进一步的证实了利用序列信息是可以有效分类蛋白质的。这3种参数优化的方法是从不同的角度出发来提高SVM的预测率,不过从预测率高低的角度看,第1种方法是3种方法中最好的,其预测率达到了88.2%,较原始预测率提高了2.8%。这说明了相对于其它方法,第一种参数优化的方法更适合在SVM处理氨基酸含量时使用。
而下一步的工作可能会着重放在提高数据集的质量和进一步改进算法提高SVM的预测率上,尤其是加入新的算法去更有效地解决QP问题。
[1]Hoppe C,Schomburg D.Prediction of protein thermostability with a direction-and distance-dependent knowledge-based potential[J].Protein Science,2005,14:2682-2692.
[2]Cheng J L,Randall A,Baldi P.Prediction of Protein Stability Changes for Single-Site Mutations Using Support Vector Machines[J].PROTEINS:Structure,Function,and Bioinformatics,2006,62:1125-1132.
[3]Zhang G Y,Fang B S.LogitBoost classifier for discriminating thermophilic and mesophilic proteins[J].Journal of Biotechnology,2007,127:417-424.
[4]Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag,1995.
[5]Cristianini N,Shawe-Taylor J.支持向量机导论[M].李国正,王猛,曾华军译,北京:电子工业出版社,2004:24-29,82 -97.
[6]Paquet U,Engelbrecht A P.Training support vector machines with particle swarms[C].IEEE World Congress ComputerIntelligence,2003:1593-1598.
[7]Peter Villiams,Sheng Li,Jiang feng,et al.Ageometrical method to improve performance of the support vector machine [C].IEEE Tramsac on neural networks,[London]:[s.n]2006:1-5.
[8]Wu S,Amari S-I.Conformal transformation of kernel functions:a data-dependent way to improve support vector machine classifiers[J].Neural Processing Letters,2002,15:59-67.
[9]Amari S,Wu S.Improving support vector machine classifiers by modifying kernel functions[J].Neural Network,1999, 12:783-789.
[10]李蓉,叶世伟,史忠植.SVM-KNN分类器——一种提高SVM分类精度的新方法[J].电子学报,2002,30(5):754-748.
LI Rong,YE Shi-wei,SHI Zhong-zhi.SVM-KNN classifier-s new method of improving the sccuracy of SVM classifier [J].ACTA ELECTRONICA SINICA,2002,30(5):754-748.
[11]LI R,WANG H N,HE H,et al.Support vector machine combined with K-nearest neighbors for solar flare forecasting [J].Chin.J.Astron.AstroPhys,2007,7(3):41-44.
[12]董春曦,饶鲜,杨绍全.基于重复训练提高SVM识别率的算法[J].系统工程与电子技术,2003,25(10):1292-1294.
DONG Chun-xi,RAO Xian,YANG Shao-quan.An algorithm to improve the recognizing rate based on retraining samples [J].Systems Engineering and Electronics,2003,25(10):1292-1294.
[13]陆振波.支持向量机Matlab工具箱1.0[EB/OL].www.dsmz.de/microorganisms/archaea_catalogue.php
(责任编辑:杨萌)
Parameters Optimization of Support Vector Machine for Discriminating Thermophilic and Mesophilic Enzyme
ZHANG Zheng-yang, XU Wen-bo*, DING Yan-rui
(School of Information Technology,Jiangnan University,Wuxi 214122,China)
It was widely accepted that amino acid composition play vital role on the protein thermostability.In this manuscript,20-amino acid composition in their protein sequence was chosen as the feature vector of SVM and used to predict the protein thermostability by SVM.the accuracy increased from 85.4%to 88.2%by using the geometrical method to optimize SVM parameter.Furthermore,it could be acquired following conclusions:(1)geometrical method is an efficient method to improve the accuracy of SVM parameters;.(2)there is a very close relationship between percentage of amino acid and enzyme thermostability.
SVM,percentage of amino acid,discrimination,parameters optimization
TP 183
:A
1673-1689(2010)02-0312-05
2009-04-11
江南大学创新团队基金项目(JNIRT0702);江南大学自然科学预研基金项目。
*通信作者:须文波(1946-),男,教授,博士生导师,主要从事人工智能、计算机控制技术、嵌入式操作系统。Email:zzylivehhit@sohu.com
