基于HPM的数学教学实践探究

●刘 超 (新疆石河子大学师范学院数学系 新疆石河子 832003)

引言

HPM(History and Pedagogy of Mathematics)意指数学史与数学教育之间的联系，它作为一个学术领域出现，始于1972年.HPM研究的目标是通过数学历史的运用，提高数学教育的水平.HPM关注的内容包括：数学与其他学科的关系、多元文化的数学、数学史与学生的认知发展、发生教学法、数学史与学生的困难、数学原始文本在教学中的应用等.

截至目前，数学史对于数学教育的重要价值已在国内得到广泛重视.数学大师吴文俊先生说数学教育与数学史是分不开的.数学方法论专家徐利治先生认为数学哲学、数学史与数学教育的结合是数学教育改革的一个重要方向.数学教育家张奠宙先生称数学史是数学教育的有机组成部分.数学教学论专家宋乃庆教授则提出数学史与数学教育相互需要、相互依存、不可分割.截至目前，国内共召开了3届数学史与数学教育会议.分别是2005年5月在西北大学召开的“第一届全国数学史与数学教育会议”;2007年4月在河北师范大学召开的“第二届全国数学史与数学教育研讨会暨第七届全国数学史会议”;2009年5月在北京师范大学召开的“第三届全国数学史与数学教育国际研讨会暨白尚恕教授文集首发式”.3届HPM会议共有来自全国30多个省、市以及国际上的有关专家、学者500余人参加，共收到论文260余篇，安排40余场大会报告，200多个分组报告.会议代表有高等院校、研究机构的专家、教师，也有来自中小学一线的数学教师;有德高望重的数学家、数学史家、数学教育家，也有初窥门庭的相关专业研究生.3届HPM会议的主题均涉及数学史的教育价值、数学史在数学教育中应用的实践开发;数学史与新课程的整合、HPM案例的研制开发、数学史研究进展、数学文化与素质教育、数学教育中数学史的运用、数学教育与数学史课程研究、HPM相关理论与案例研究、外国数学史(包括比较数学史)、中国数学史、数学史与数学教育的国际比较研究等［1-3］.此外，国内各类期刊中的HPM文章也逐渐增多，表现出HPM研究的良好前景.

但是，作为一个研究领域，大家对HPM的功能与作用的认识显得比较混乱，有些内容显然偏离了HPM作为数学与数学教学中介的研究领域.例如国内许多HPM方面的学术论文主要探讨在数学课程中添加数学史料，以激发学生的学习兴趣，进行爱国主义教育等.这些论述大都停留在表面上，没有起到数学史应有的作用和育人功能.实际上，作为数学走向数学教学的中介，HPM的功能在于通过数学史寻找数学教育的规律和经验，把数学知识的历史形态加工整理成教师和学生能够方便使用的教育形态，使数学史为生动活泼的数学教学服务.随着HPM研究的深入开展，数学史为数学教育服务需要从理论走向实践，学术界也日益注重数学史融入数学教学的可操作性具体方法的探讨［4］.本文拟给出以下几种具体的操作方法，旨在抛砖引玉，以期有更多的、更有效的数学史与数学教育整合方式的产生.同时，不容忽视的是，一线教师是HPM理念付诸实施的最佳人选，加强教师的数学史修养必须提到议事日程上来.

1 “数学史—归纳”方式

教学流程 提出问题→回顾历史→重演历史(过程呈现→归纳总结)→形成定理、公式、方法→定理、公式、方法的运用.

具体操作 第1步，在教学开始时先设置问题情境，经过学生分析和推敲，教师提出或学生自己得出这节课所要面对的和要解决的问题;第2步，教师向学生介绍与这个问题相关的历史背景;第3步，呈现历史上对这个问题的思考、解决方法，学生在教师的引导下进行总结;第4步，形成对这个问题的正确认识，形成定理、公式、方法;第5步，在归纳出概念、定理、方法的基础上，运用其解决问题，以加深理解.

教学实例 二次方程ax2+bx+c=0(a≠0)求根公式的推导.

教科书中是利用配方法给出ax2+bx+c=0(a≠0)求根公式的：

然而在代数学发展的初期，许多代数问题是利用几何知识解决的.下面重现古埃及推导二次方程求根公式的方法.先提出如下问题：一正方形与一以此正方形边为宽的长方形(长为b)面积之和为c，求正方形的边长.

由于尼罗河的定期泛滥，土地测量人员不得不多次丈量土地，久而久之，即形成了利用“出入相补”原理推导二次方程求根公式的方法［5］.

进行如图1所示的操作，将长方形分割为2个相等的小长方形，把其中一个小长方形放到正方形

图1

如何解ax2+bx=c(a≠0)?不难发现，若将

特点分析 “数学史—归纳”方式是以历史为背景，以大量比较一致的史料为题材，对教学的内容进行分析、概括和提炼，归纳抽取出定理、公式、方法.这是数学史教学的常用方式，它比较简单、便捷.上课时，教师娓娓道来，学生的思维强度较低，有很好的故事性和情趣性.学生学习时能获得良好的心理感受，在故事中略作思考，通过归纳，便可得出结论.这一方式比较适合于低年级学生，或者作为理性抽象的数学课堂的一种调节，其简单的操作方式完全符合全民普及性教育、科学素养提升、人文和科学结合的时代要求.

2 “数学史—冲突会话”方式

教学流程 提出问题→回顾历史→重演历史(呈现观点→形成冲突→会话辨析)→建立概念、定理、方法→概念、定理、方法的运用.

具体操作 第1步、第2步同上.第3步，提供历史上对这个问题的思考、相矛盾的观点，并提供相关的原始文献，让学生形成强烈的思维冲突.静心思考后，学生分成两派进行对话、辩论.根据实际情况，教师可以作为思维的引导点拨者、辅助者，也可以是弱派的支持者，并可变换立场，使辩论均衡，也可以成为老观念的卫道者.所谓真理越辩越明，最后慢慢让全班的学生立场都站到正确的或更具优势的认识上.第4步，表达出正确的观念，让学生在会话辨析中建构新的概念、规律.第5步，同上.

教学实例 负数教学

尽管负数及其运算法则在16世纪就已经产生，但直到19世纪，数学家仍然不用负数.在他们看来负数是荒谬的，负数是否是“数量”?一个小于0的“数量”表示什么?历史上的数学家因为找不到负数的对应物，而不能理解它，甚至拒绝接受它，但他们又无法否认负数在形式推导上是正确的.因此，有的数学家虽在思想上不承认它，但仍然让它参与数量运算.数学家之所以迟迟不能接受负数，是因为在数轴上表示数时，仅仅认为数具有大小的特征，而没有看到它们在数轴上又表现为一种顺序关系;不仅在数轴的正向有顺序关系，在数轴的反向也具有顺序关系.数学家只有在用负数来表示亏损或负债的时候，才能理解负数的现实意义，才认识到数在另一个方向上也有大小和顺序，才承认负数是客观实在的数.这也是学生学习负数必然要克服的“认识论障碍”.

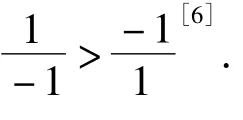
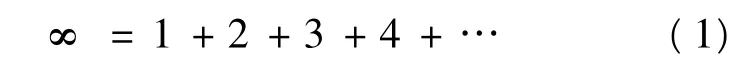
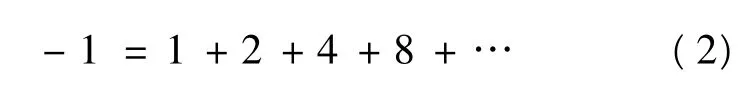
特点分析会话是协作过程中不可缺少的环节，是达到意义建构的重要手段之一.采用“数学史—冲突会话”的教学方式，逐步养成学生敢于质疑、善于交流、乐于合作的科学态度.同时，针对一些抽象的概念、规律设计一些讨论题，可以使学生对问题的认识更为清晰，从而使知识成为思维的必然结果.事实上，这种教学模式对师生的要求都很高.它要求教师深刻领会先哲的观点，特别是“错误观点”;要求学生具有较好的科学理性和思辨能力，让学生认识到：错误也有合理性，正确只是更具优越性，理论是不断发展的和没有终结的.

3 “数学史—探究”方式

教学流程 提出问题→回顾历史→重演历史(猜想与假设→设计实验→进行实验→分析与论证)→“创造公式、方法”→公式、方法的运用.

具体操作第1步、第2步同上.第3步，提供历史上对这个问题的思考、实例以及历史上对这个问题提出的猜想或假说.根据这个猜想与假说提出方案，设计实验，并进行实际操作，记录数据，分析论证结果.第4步，引导学生建立和创造公式、方法.第5步，同上.

教学实例勾股定理

教师首先引入勾股定理，介绍数学史上是如何发现勾股定理的.设计实验，让学生独立发现勾股定理.为使实验便于操作，可以工作单的形式给出具体的操作流程.

工作单1在方格纸内斜放一个正方形，正方形的4个顶点都在格点上，每个小方格的边长为1个单位长度，怎样计算正方形的面积?

工作单2直角三角形的2条直角边和斜边之间有什么关系?用前面的方法进行试验，分别计算2条直角边的平方与斜边的平方.将得到的数据列表，猜测2条直角边与斜边之间可能的关系.

工作单3直角三角形2条直角边的平方和等于斜边的平方，这一命题是从以上几个特殊例子中得出的.对于一般的直角三角形，它是否成立呢?请同学们选择一般的直角三角形，仍用上面的方法加以验证.

工作单4请用直角边长为a，b，斜边长为c的4个直角三角形，拼成至少含有一个正方形的正方形，并比较不同拼图之间的面积关系.此举是启发学生计算各种拼图的面积，得到另一种关于勾股定理的确认.

工作单5变式练习，加强对勾股定理的掌握和灵活运用.

特点分析“数学史—探究”方式是对历史最具体的重演，是很好的过程体验教学方式.重演的过程中蕴涵了大量的方法和哲学思想.这些深刻的数学思想会对学生科学素养的提高起到积极有效的作用.通过实验，用铁的事实告诉学生正确的科学规律.整个过程能充分体现出数学的学科特征，这也是“数学史—探究”方式最需要体现的过程和思想.“数学史—探究”方式的教学过程往往比较费时、费力，同时也要求对应的数学史内容本身具有很深刻的方法和思想.教师要充分准备，深入了解历史事件，并在遵从历史事实的基础上，作出合理取舍，设计出符合中学生思维和认识水平的教学方案，让学生感受教学过程，对学生能力和素质的提高具有积极意义.

4 教师的数学史修养是HPM理念付诸实施的必要前提

数学史与数学教育整合的理念对于数学教育有着重要的现实意义.数学史对于数学教学来说是一种十分有效、不可或缺的工具.历史能够帮助教师按自然的顺序呈现各个数学概念，尽可能地减小各个知识点之间的跨越度，为开展课堂活动提供生动而有意义的资料.尽管数学史对于数学教育的作用已逐渐得到广大数学教育工作者的肯定，但课堂教学的实践却多少有些让人气馁.研究发现，数学史融入中学数学课堂教学的现状不容乐观.在中学，大部分教师都是按照课本的要求进行教学的，很少有教师寻求各部分知识在历史上是如何出现的，课本为什么以这种方式来呈现，怎么把课本上呈现的知识与历史上知识产生的过程去结合?究其原因，在于在数学教学中融入数学史面临诸多困难，而这些困难直接影响着HPM的理想的实现.而在这诸多的困难中，首当其冲地是中学一线教师缺乏必要的历史知识.造成教师数学史知识缺乏的一个直接原因是缺少这方面的教育.尽管数学史已被公认为师范教育以及大中学校学生自由教育中的重要学科，但从世界范围看，在教师教育过程中数学史课程是普遍被忽视的，即便是开设了数学史课程，对数学史的教育也很少关注.

我们认为，为了实现数学史与课堂教学的有效整合，首先，教师必须了解本学科的基本发展史.实际上，在教师教育的计划中，开设数学史的课程应该是教育取向的数学史课程.数学史教育者，尤其是教师教育者的一个重要任务就是精心选择那些和教师将来的教学有关的数学史知识，并对它们的教育意义加以分析.这个任务，需要联合数学史家和数学教育家的共同力量来完成.在这个基础上，确定其中关键的发展步骤，譬如一些认知障碍的出现.然后再按照课堂和学生的实际情况重新构建这些关键步骤，直接或间接地使用历史材料设计教学方案.历史资料是教学设计、教学实验的灵感来源和控制手段，但是使用历史并非简单地重复历史事件或评论历史事实，正如弗莱登塔尔所说：我们不应该重蹈发明者的足迹，而是通过改良使历史过程有更好的引导作用［7］.对于一线教师来说，必须谨慎地对待历史和教学，需考虑到2种环境的不同：历史与课堂的优势和局限分别是什么.只有做好两手充分准备，才能根据不同水平、不同类型的学生，恰如其分地将历史的资料转化为教学的材料.

鉴于以上分析，在高师院校对未来的数学教师开设数学史课程是非常必要的，特别是开设的课程要注重挖掘数学史料的教育价值.另外，对于在职教师而言，以各种形式提高他们的数学史修养也非常必要.可效仿国际上比较常用的方式，考虑以学校为中心，组织教师开展HPM的实践活动，这不仅可以增强教师的HPM素养，而且还可以促进他们在各方面的专业发展［8］.此外，将HPM专题作为在职教师培训的一个新课程也是可取的.

［1］ 第一届全国数学史与数学教育会议论文集［C］.西安：西北大学，2005.

［2］ 第二届全国数学史与数学教育会议论文集［C］.石家庄：河北师范大学，2007.

［3］ 第三届全国数学史与数学教育会议论文集［C］.北京：北京师范大学，2009.

［4］ 汪晓勤，张晓明.HPM研究的内容与方法［J］.数学教育学报，2006，15(2)：16-18.

［5］ 李文林.数学史概论［M］.北京：高等教育出版社，2002：33-35.

［6］ 刘超.负数的历史及其启示［J］.中学生数学，2009(5)：24-25.

［7］ Freudenthal H.Didactical Phenomenology of Mathematical Structures［M］. Dordrecht：Reidel Publishing Company，1983：133.

［8］ John Fauvel，Maanen J.Van.History in the Mathematics Education［M］.Dordrecht：Kluwer Acadejic Publishers，2000.