2道竞赛题的背景探讨

●郝志刚 (连云港外国语学校 江苏连云港 222006)

文献［1］中定义：有外接圆且2组对边的乘积相等的四边形称为调和四边形.

下面探讨2道数学竞赛试题的命题背景.

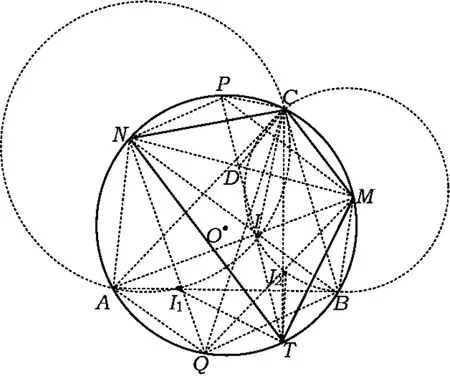
图1

探讨1 如图1所示，在⊙O的内接四边形TMCN中，NC·MT=MC·NT(四边形TMCN为调和四边形).连结TC，MN，由托勒密(Ptolemy)定理

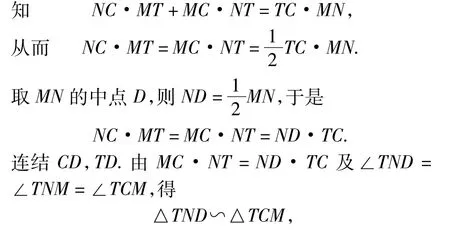
由∠MDC=∠MDT，知 MN是∠CDT的对称轴，于是点C关于MN的对称点I必在DT上，从而MN垂直平分CI.

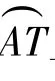
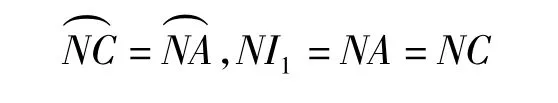
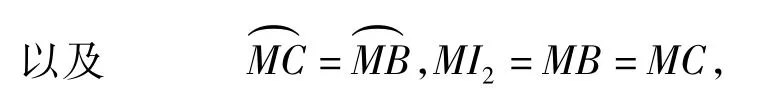
即知I1是△AQC的内心，I2是△QCB的内心.

连结 TI1，TI2.由 NC·MT=MC·NT 以及NC=NI1，MC=MI2，得

通过以上对调和四边形的讨论，可构成如下竞赛题：

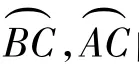
(1)MP·MT=NP·NT;

(2)在弧)AB(不含点C)上任取一点Q(Q≠A，T，B)，记△AQC，△QCB 的内心分别为 I1，I2，则点Q，I1，I2，T 共圆.

(2009年全国高中数学联赛加试试题)

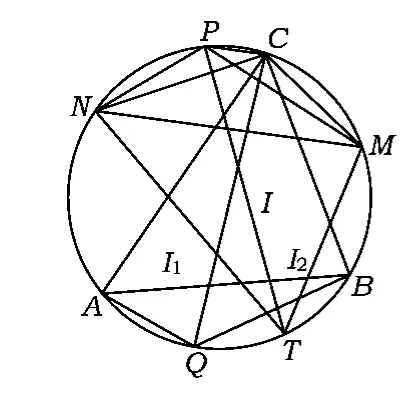
图2

图3

探讨2 如图3，在调和四边形ABCD中，由

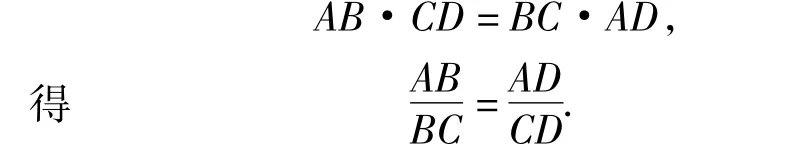
连结AC，令∠ABC的平分线交AC于点E，连结DE，则BE平分∠ABC等价于

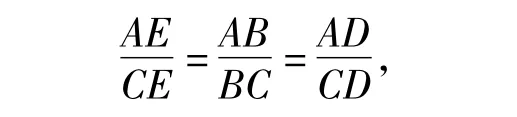
即DE平分∠ADC，于是∠ABC的平分线、∠ADC的平分线和AC三线共点的充要条件是

AB·CD=BC·AD.

连结DB，过点D作DP⊥BC于点P，作 DQ⊥AC于点Q，作DR⊥AB于点R，则由西姆松(Simson)线定理，知垂足P，Q，R这3个点共线.

注意到∠DPC+∠DQC=180°以及∠DQA=∠DRA=90°，即知点 D，P，C，Q 与 D，Q，R，A 分别共圆，结合点 A，B，C，D 共圆，得

于是PQ=QR的充分必要条件为

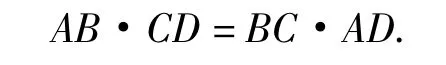
至此，又可构成如下竞赛题：

赛题2 设ABCD是一个圆内接四边形，从点D向直线BC，AC和AB作垂线，其垂足分别为P，Q和R.证明：PQ=QR的充要条件是∠ABC的平分线、∠ADC的平分线和AC这3条直线相交于一点. (第44届国际数学奥林匹克竞赛试题)

综上不难看出，命题者从经典图形(调和四边形)与著名定理(托勒密定理和西姆松线定理)出发，深入探究，推陈出新，演变出2道数学奥林匹克试题，构思巧妙、新颖，其命题背景是非常深刻的.同时也容易看出，笔者对命题构思的过程的研究，实际上就是笔者探究性学习的过程.这种研究性学习，对数学教师的研究能力和综合知识的提高很有帮助.从中也可启发教师把这种探究学习的能力迁移到新课标所倡导的、在合作与探究学习中培养学生综合能力的教学理念的落实与培养，最终达到全面提升师生的研究和学习能力.

［1］ 梁绍鸿.初等数学复习及研究(平面几何)［M］.北京：人民教育出版社，1958.