浅谈函数思想在数学高考试题中的应用

●田华钦 (缙云县第二中学 浙江缙云 321400)

函数思想是高中数学的一条主线，函数与方程思想也是数学最本质的思想之一.高中数学中的初等函数、数列、不等式、解析几何等问题都可以转化为函数问题求解.

函数思想就是用变量和函数来思考问题的方法.函数与方程有时又可以转化，函数思想涉及的知识点多、知识面广，在概念、应用、理解都方面有一定的要求，应用非常广泛，是高考考查的重点.

笔者就几道高考试题浅谈函数思想在解决不等式、函数零点、解析几何、参数的取值范围等问题中的应用，供参考.

1 运用函数思想解决不等式问题

函数与不等式之间有着密不可分的联系，在不等式问题中，应重视以函数为桥梁，根据实际问题建立函数模型，用函数思想分析、解决问题.

(1)对于任意实数x，f'(x)＞m恒成立，求m的最大值;

(2)若方程f(x)=0有且仅有1个实根，求a的取值范围.

(2009年江西省数学高考文科试题)

解(1)f'(x)=3x2-9x+6.因为x∈(-∞，+∞)，f'(x)≥m恒成立，所以m只要小于等于f'(x)的最小值即可.又因为

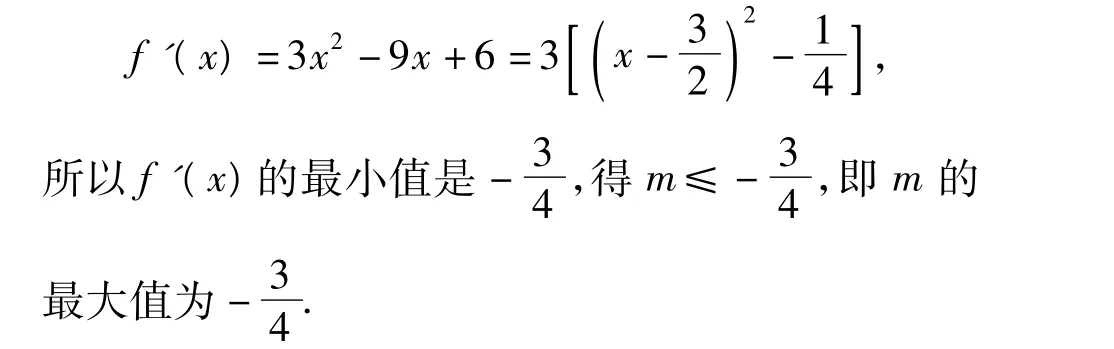
(2)略.

2 运用函数思想解决函数零点问题

函数零点就是方程的解，方程解的个数转化成函数图像与横轴交点的个数，方程在某个区间上有解的问题经常转化成求函数的值域问题.

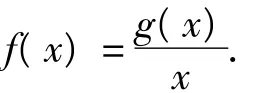
(1)若曲线y=f(x)上的点P到点Q(0，2)的距离的最小值为，求m的值;

(2)当k(k∈R)如何取值时，函数y=f(x)-kx存在零点，并求出零点.

(2009年广东省数学高考理科试题)

解(1)略.

3 运用函数与方程思想解决解析几何问题

解析几何即用代数方法研究几何问题，可把其中的曲线解析式看作方程，通过解方程的手段或对方程的研究使问题得以解决.对于曲线上的动点问题，线段长度、面积大小的最值问题，其在变化过程中会引入一些相互联系、相互制约的变量，从而使变量与其中的参数之间构成函数关系，转化成函数问题解决.

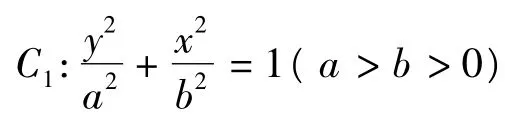
(1)求椭圆C1的方程.

(2)设点 P在抛物线 C2：y=x2+h(h∈R)上，C2在点 P处的切线与C1交于点M，N.当线段AP的中点与MN的中点的横坐标相等时，求h的最小值.

(2009年浙江省数学高考理科试题)解 (1)由题意得

图1

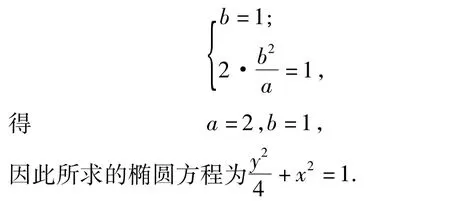
(2)不妨设 M(x1，y1)，N(x2，y2)，P(t，t2+h)，则抛物线C2在点P处的切线斜率为y'|x=t=2t.直线MN的方程为y=2tx-t2+h，将上式代入椭圆C1的方程，得

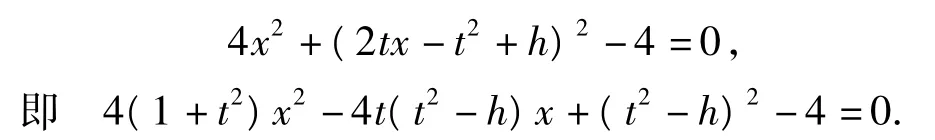
因为直线MN与椭圆C1有2个不同的交点，所以

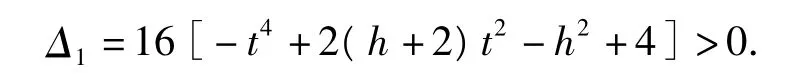
设线段MN中点的横坐标是x3，则

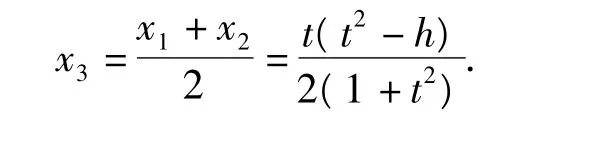
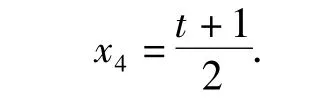
由题意得x3=x4，即成立，故h的最小值为1.

4 运用函数思想求参数(或变量)的范围

在一个含有多个变量的数学问题中，需要确定合适的变量和参数，从而揭示函数关系，使问题更加明朗化.或者在含有参数的函数中，将函数自变量作为参数，而参数作为函数的自变量，更具有灵活性，从而巧妙地解决有关问题.

设线段PA中点的横坐标是x4，则f'(-1)=0.

(1)试用含a的代数式表示b，并求f(x)的单调区间.

(2)令 a=-1，设函数 f(x)在 x1，x2(x1＜ x2)处取得极值，记点 M(x1，f(x1))，N(x2，f(x2)，P(m，f(m))，x1＜m ＜x2.请仔细观察曲线 f(x)在点P处的切线与线段MP的位置变化趋势，并解释以下问题：

①若对任意的m∈(x1，x2)，线段MP与曲线f(x)均有异于点M，P的公共点，试确定t的最小值，并证明你的结论;

②若存在点Q(n，f(n))，x≤n＜m，使得线段PQ与曲线f(x)有异于点P，Q的公共点，请直接写出m的取值范围(不必给出求解过程).

(2009年福建省数学高考文科试题)

解(1)略.

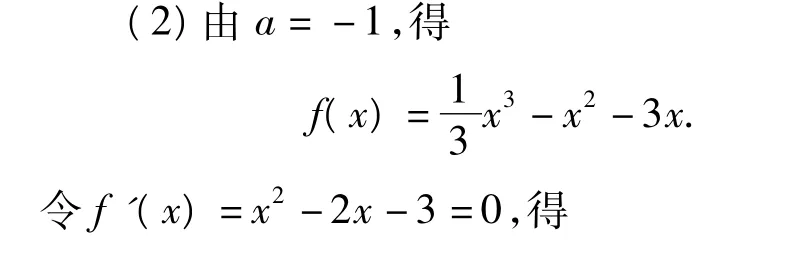
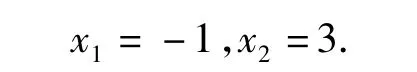
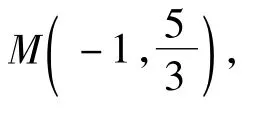
①直线MP的方程为

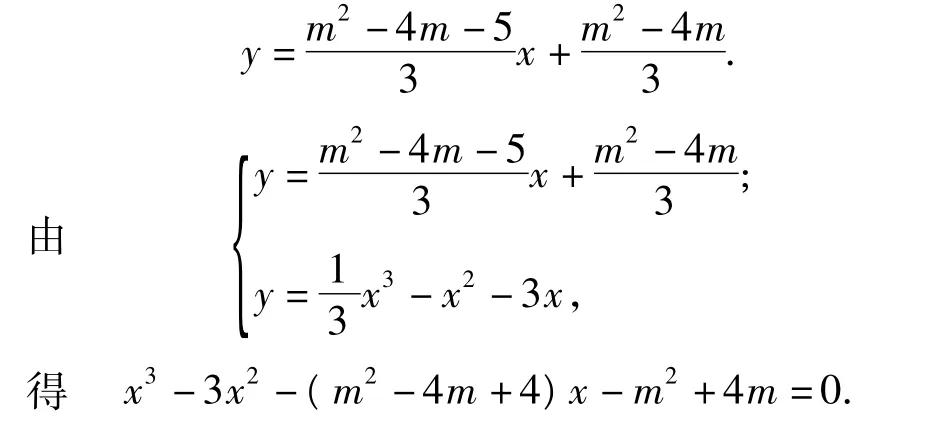
线段MP与曲线f(x)有异于点M，P的公共点等价于上述方程在(-1，m)上有根，即函数

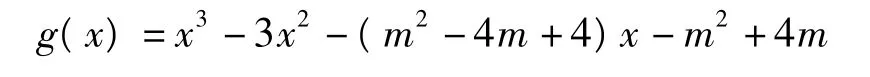
在(-1，m)上有零点.因为函数g(x)为三次函数，所以g(x)至多有3个零点，2个极值点.又

所以g(x)在(-1，m)上有零点等价于 g(x)在(-1，m)内恰有1个极大值点和1个极小值点，即

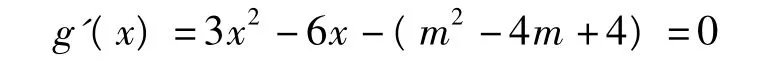
在(1，m)内有2个不相等的实数根.于是

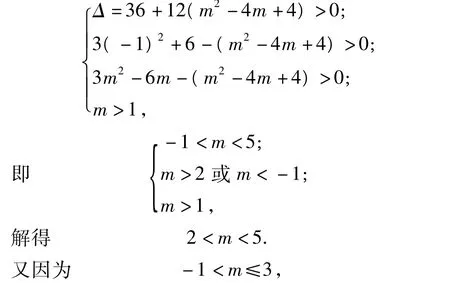
所以m的取值范围为(2，3］，故满足题设条件的t的最小值为2.

②略.

从上述高考试题可以看出：函数思想的应用相当广泛.在解题时，要善于对所给的问题仔细观察、深入分析，挖掘题目中的隐含条件，构造出函数解析式和妙用函数的性质去解决问题.在平时的教学中，必须重视函数思想方法的落实，让学生更好地掌握这个内容.