利用均值不等式证明轮换不等式

●周 江 (康定中学 四川康定 626000)

轮换不等式的证明方法很多，技巧性也很强.下面例举一种“凑”的方法，即根据轮换不等式取等的条件是相等.只要领悟“凑”的技巧，这类不等式完全可以程序化证明.

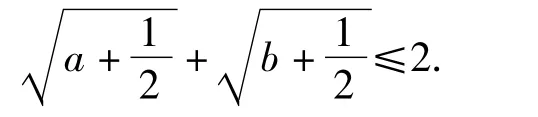
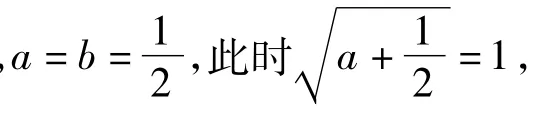
同理可得

两式相加得

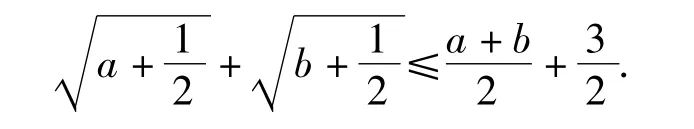
结合 a+b=1，得

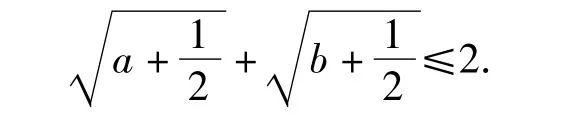
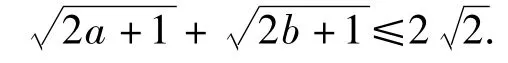
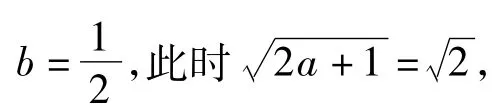
同理可得

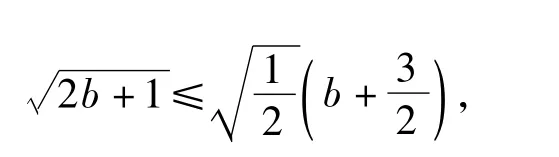
结合 a+b=1，得

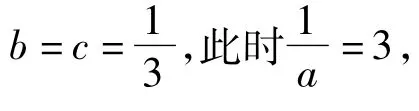
变式1 在△ABC中，角A，B，C满足cos2A+cos2B+cos2C=1，求证：

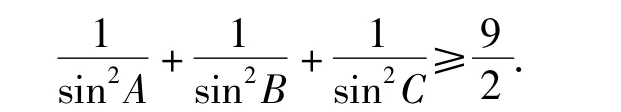
分析cos2A+cos2B+cos2C=1等价于

要使不等式成立，必须满足

变式2 设 x1，x2，…，xn是正数，且 x1+x2+…+xn=1，求证：

变式3 已知si＞ 0(i=1，2，…，n)，s1+s2+… +sn=A，证明：

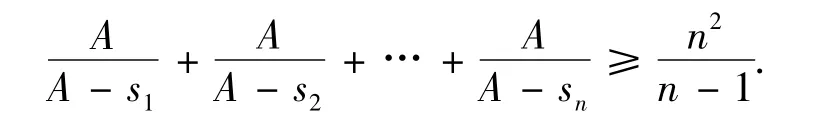
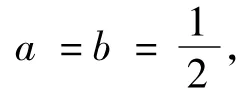
变式2 已知a＞0，b＞0，a+b=1，求证：

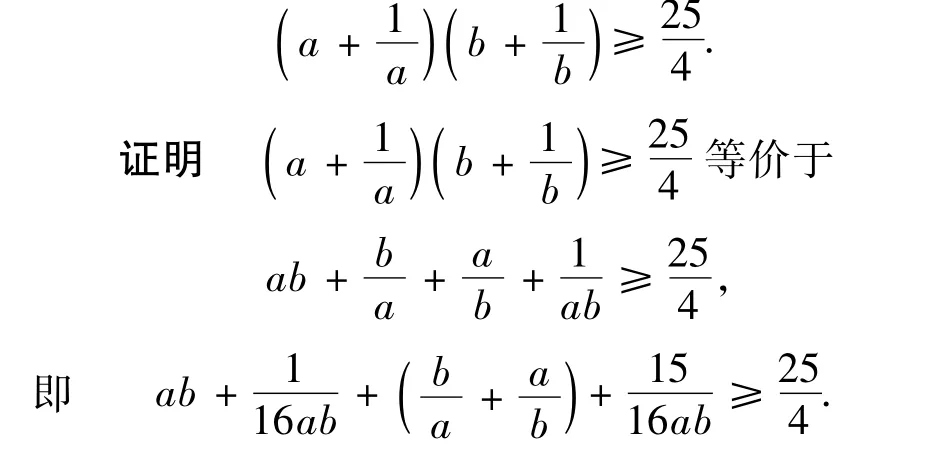
例4 证明不等式：

证明设a1+a2+… +an=a，则