简析函数对称性和周期性的关系

●周少锋 (嵊州市第一中学 浙江嵊州 312400)

函数内容贯穿于高中数学的始终，历来是高考考查的难点和热点，要求学生熟练掌握函数的性质.但在学习过程中，许多学生都被函数的若干性质弄得头昏脑涨.事实上，只要把握好其中的关系，就不难解决了.函数的这些性质到底有哪些相互关系呢?这里就以函数图像的对称性和周期性为例，探讨它们之间的关系.

在学习三角函数知识时，我们知道三角函数是周期函数，它的变化过程是周期性不断重复的.以下2条性质已是人所共知的函数性质，在研究函数图像的对称性和周期性时，若以三角函数为例，则更容易理解.

性质1 若函数f(x)满足f(a+x)=f(a-x)(或f(2a-x)=f(x))，x∈D(D是函数f(x)的定义域)，则函数f(x)的图像关于直线x=a对称.

性质2 若函数f(x)满足f(a+x)=-f(ax)(或f(2a-x)=-f(x))，x∈D(D是函数f(x)的定义域)，则函数f(x)的图像关于点(a，0)对称.

对于这2条性质与函数周期性的关系，讨论得不多.本文试图就这2个方面作一些探索，求教于同行.

1 由函数的对称性讨论周期性

定理1 若函数f(x)的图像关于直线x=a对称，且f(x)的图像又关于直线x=b对称(a≠b)，则函数f(x)是一个周期函数，且周期T=2k(ba)(k∈Z，k≠0).

证明因为f(x)的图像关于直线x=a对称，且关于直线x=b对称(a≠b)，所以对于任意t∈R，有

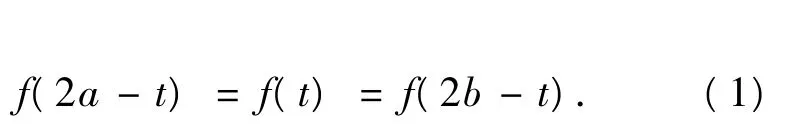
令 2b-t=x，则

代入式(1)得

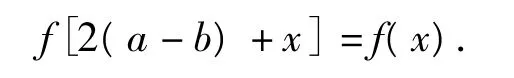
又由 a≠b，得

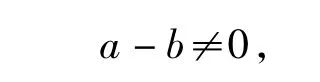
因此f(x)的周期是 T=2k(b-a)(k∈Z，k≠0).

例1 设函数f(x)在(-∞，+∞)上满足

且在闭区间［0，7］上，只有 f(1)=f(3)=0.

(1)试判断函数y=f(x)的奇偶性;

(2)试求方程f(x)=0在闭区间［-2 005，2 005］上的根的个数，并证明你的结论.

(2005年广东省数学高考理科试题)

分析(1)由 f(2-x)=f(2+x)，f(7-x)=f(7+x)，知函数f(x)关于直线x=2和x=7对称.从而由定理1知函数y=f(x)是周期函数，且周期为 T=2k(7-2)=10k.又

故函数y=f(x)是非奇非偶函数.

(2)又 f(3)=f(1)=0，f(11)=f(13)=f(-7)=f(-9)=0，故 f(x)在［0，10］和［-10，0］上均有2个解，从而可知函数y=f(x)在［0，2 005］上有402个解，在［-2 005，0］上有400个解，所以函数y=f(x)在［-2 005，2 005］上有802个解.

定理2 若函数f(x)的图像关于点A(a，0)对称，且f(x)的图像又关于点 B(b，0)对称(a≠b)，则函数f(x)是一个周期函数，且周期T=2k(ba)(k∈Z，k≠0).

证明f(x)的图像关于点 A(a，0)和 B(b，0)都对称，故对于任意t∈R，有

令 x=2b-t，则

代入式(2)得

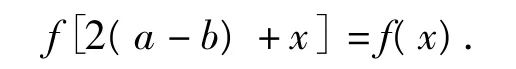
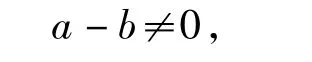
又由 a≠b，得从而f(x)是以T=2k(b-a)(k∈Z，k≠0)为周期的周期函数.

例2 函数f(x)的定义域为R，若f(x+1)与f(x-1)都是奇函数，则 ( )

A.f(x)是偶函数 B.f(x)是奇函数

C.f(x)=f(x+2) D.f(x+3)是奇函数

(2009年全国数学高考理科试题Ⅰ)

分析由f(x+1)是奇函数，可知f(x)关于点(1，0)对称;由f(x-1)是奇函数，可知f(x)关于点(-1，0)对称.又由定理2知，f(x)是一个周期函数，且周期

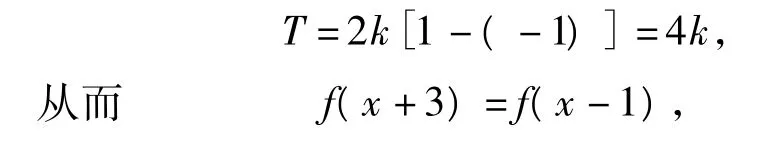
故选D.

例3 已知f(x)是R上的偶函数，g(x)是R上的奇函数，且g(x)=f(x-1)，若f(-2)=a(a为常数)，则f(2 002)= _______.

分析由已知得

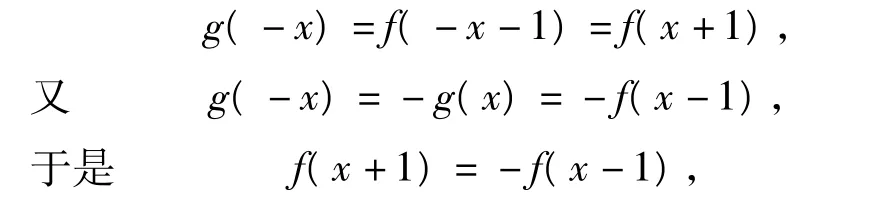
故f(x)关于点(1，0)对称.因为f(x)是偶函数，所以f(x)也关于点(-1，0)对称.由定理2知，f(x)是一个周期函数，且周期

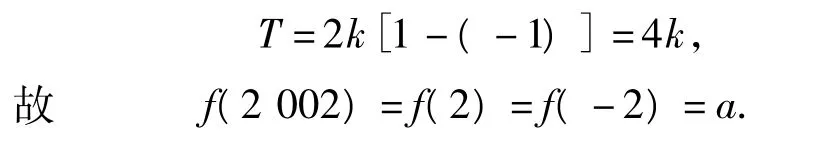
定理3 若函数f(x)的图像关于直线x=a对称，且f(x)的图像又关于点(b，0)对称(a≠b)，则函数f(x)是一个周期函数，且周期T=4k(b-a)(k∈Z，k≠0).

证明由函数f(x)的图像关于直线x=a对称，且f(x)的图像又关于点(b，0)对称(a≠b)，得

因此f(x)是以T=4k(b-a)(k∈Z，k≠0)为周期的周期函数.

A.-2 B.-1 C.0 D.1

(2010年浙江省绍兴市统考试题)

得f(x)是偶函数.由定理3知，函数f(x)是周期函数，且周期为

2 由函数的周期性讨论对称性

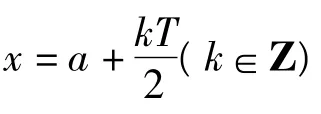
证明由函数f(x)的图像关于直线x=a对称，且f(x)是周期为T的周期函数，得

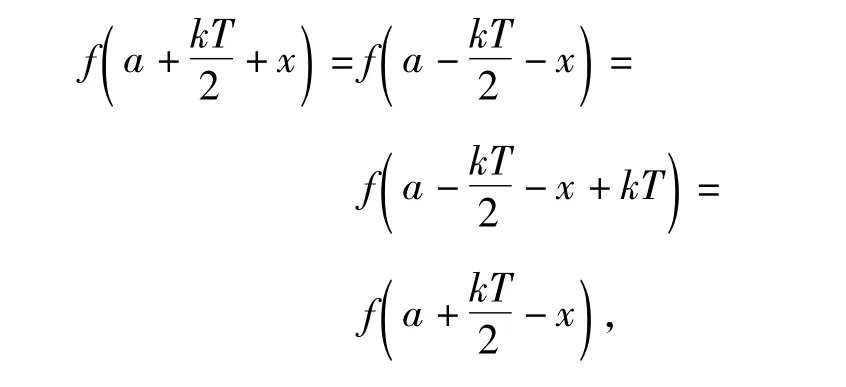
例5 已知定义在R上的奇函数 f(x)满足f(x-4)=-f(x)，且在区间［0，2］上是增函数.若方程f(x)=m(m＞0)在区间［-8，8］上有4 个不同的根 x1，x2，x3，x4，则x1+x2+x3+x4= _______.

图1

(2009年山东省数学高考理科试题)

分析因为定义在R上的奇函数满足f(x-4)=-f(x)，所以

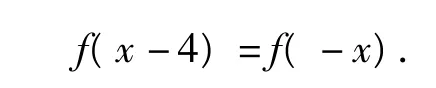
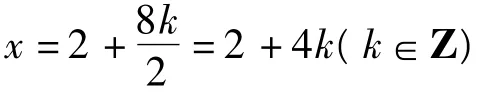
由点x3，x4关于直线x=2对称，得

证明函数f(x)的图像关于点(a，0)对称，且f(x)是周期为T的周期函数，从而

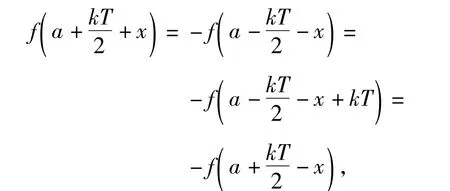
例6 定义在R上的函数f(x)既是奇函数，又是周期函数，3是它的一个正周期.若将方程f(x)=0在闭区间(0，6)上的根的个数记为n，则n可能为 ( )

A.0 B.1 C.3 D.5

(2007年安徽省数学高考理科试题)

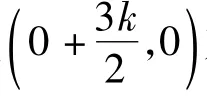
但以下2个命题却不一定成立.

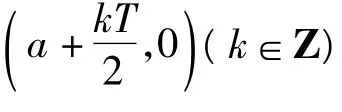
反例：f(x)=|tanx|只有对称轴，但没有对称中心.

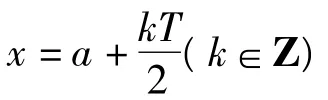
反例：f(x)=tanx只有对称中心，没有对称轴.

注若已经知道函数f(x)既有对称中心，也有对称轴，则以上2个命题均成立.

综上可知，认识函数对称性和周期性可使我们对函数的图像特征与性质有比较清晰的认识，克服对函数(特别是抽象函数)恐惧的心理，从而进一步引导学生解题思想方法的探求，提高解决问题的能力，培养思维的灵活性，最终达到培养创新思维的目标.

［1］ 王国云.抽象函数的对称性与周期性刍议［J］.中学教研，2010(6)：31-33.

［2］ 侯立刚.例析函数中十二对易混问题［J］.数理化解题研究，2009(1)：1.

［3］ 张建国.函数图像的对称性与其周期的教学［J］.上海中学数学，2009(6)：14.