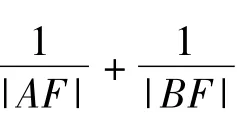让课本习题成为数学探究的鲜活资源

●钮兆岭 (淮阴师院附属中学 江苏淮安 223001)

《普通高中数学课程标准(实验)》明确指出：“数学探究是贯穿于整个高中数学课程的重要内容，渗透在每一个模块或专题中”.又指出“倡导积极主动、勇于探索的学习方式”是新课程的基本理念之一，学生的数学学习活动不应只限于接受、记忆、模仿和训练.高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.因此，探究式教学应成为数学课堂教学的主要方式之一，应该成为培养学生探究意识的主渠道、主阵地.课本习题是几经编者筛选命制而成的，具有一定的代表性、典型性、探究性，是组织探究活动的有效载体，是培养学生探究意识的再生资源，值得教师重视.笔者选择了苏教版普通高中课程标准实验教科书选修2-1中的一道习题，组织学生进行了一次有意义的探究活动.通过这次探究笔者感受到：用好课本习题对提高教学质量、培养学生的思维能力具有非常重要的意义.为行文方便，将原题附录以下：

例1 过抛物线y2=2px(p＞0)的焦点的一条直线和抛物线有2个交点，且2个交点的纵坐标分别为 y1，y2，求证：y1y2=-p2.

从题目涉及的内容看，有直线方程、抛物线方程、方程组的解法，一元二次方程根与系数关系的应用，具有一定的综合性，进行探究有助于沟通知识间的内在联系，有利于优化知识结构;从动、静的角度看，抛物线是相对静止的，直线AB是运动的，进行探究有助于学生动中窥静，静中窥动;从原题给出的结论看：y1，y2是可变的，y1y2是不变的，进行探究有利于培养学生用运动、变化的观点去思考问题;从原题的解决途径看，有利于培养学生思维的灵活性与深刻性.

1 合作探究，寻觅多种解法

出示题目，让学生思考、讨论，教师巡视点拨，适时介入.当大部分学生基本完成本题解答时，教师请学生陈述解题思路.

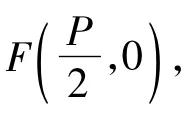
由韦达定理得

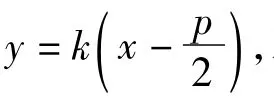
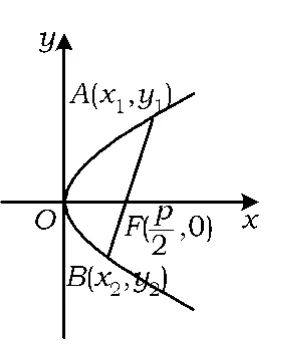
图1

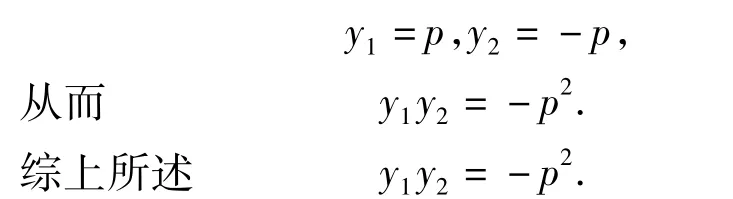
T1：S2的补充指出了部分学生解决这类问题的思维缺陷，今后用到含有斜率k的直线方程时应考虑斜率k不存在的情况.S1，你是怎么想到这一方法的?

S1：这是一道有关直线与抛物线位置关系问题，求证的结论是2个交点纵坐标之积为常数，这使我联想到一元二次方程中的韦达定理.

T：S1根据直线与抛物线相交及题中结论呈现的形式联想到一元二次方程根与系数的关系，是寻觅问题解决切入点的好办法.此题还有别的解法吗?

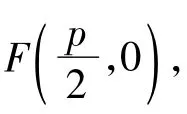
又因为y1≠y2，所以必有 y1y2=-p2.当 AB⊥x轴时，方法如S2所述.

综合上述2种情况可知结论成立.

T：你是怎么想到这一方法的?

S：直线AB过焦点 F实际上隐含着点 A，F，B共线，利用斜率相等可构造方程.为了减少未知数的个数，利用点A，B在抛物线上，将2个点的横坐标用含有y1，y2的式子表示，可简化解题过程.

T：S3的思路有创意，对解题活动的开展很有启发，利用已知条件减少未知量的个数，挖掘题目中隐含的条件构造方程.这体现了用方程思想解决问题的意识，拓宽了解题途径.

S4：还可以用几何知识解决.如图2，过点A，B分别作抛物线准线l的垂线，垂足分别为A1，B1.因为AB过点F，由抛物线定义得|AA1|=|AF|，所以∠1=∠2.又 AA1∥FK，得∠1=∠3，从而∠2=∠3.同理可得∠4=∠5，因此∠A1FB1=90°.又由KF⊥A1B1，可得

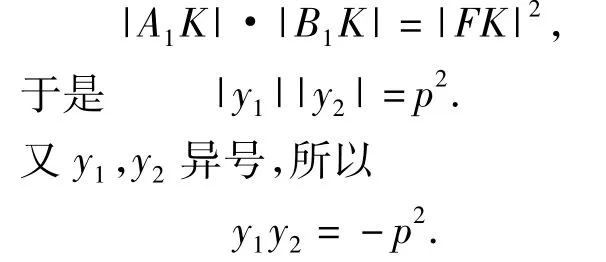
T：你是怎么想到这一方法的?

S2：通过画图可以发现

图2

从而联想到这种证法.

T：通过画图，直观地发现要证的结论，这是几何直观给我们带来的福音，它使我们容易看清问题的本质.S4的想法体现了数形转换的思想，值得倡导.还有别的解法吗?

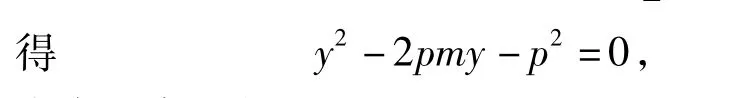
由韦达定理得

T：此解法太妙了!S5避开了选择斜率k为参数时对AB⊥x轴的讨论，这启发我们在选择方法时，要尽可能地避开讨论，减少失误.

教学感悟学生的思维是活跃的，在课堂教学中如何让学生打开思维的闸门，这就要求教师在课前对习题研究和在课堂上积极引导.优秀教师的功夫在课外，效率在课内.学生的成就感在于对问题的不断解决，学生的快乐源泉在于不断找到新方法.学生在愉悦的心境中思维效率最高，更容易催生学习的智慧.

2 选准入口，探求新型结论

通过一道课本习题，获得4种解法(S1，S2的解法合一)，令人欢欣鼓舞.若就此收场，则实在有余味未尽之感.从原题的结论看，2个交点的纵坐标之积为定值，使人联想：2个交点的横坐标之积是否为定值?|AF|和|BF|之间又会有怎样的关系?还会有其他什么结论?这些问题同样值得思考.

T：从原题结论呈现的形式看，你能猜想出原题还可能会有什么结论?

S6：若原题中2个交点的横坐标分别为x1，x2，则通过类比，可能有x1x2为定值.

T：你能猜出定值吗?

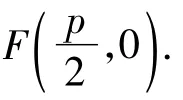
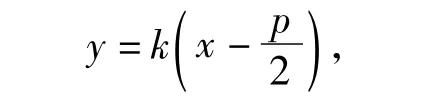
将其代入y2=2px得

由韦达定理得

S8：当AB不垂直于 x轴时，由点 A，B，F共线可得

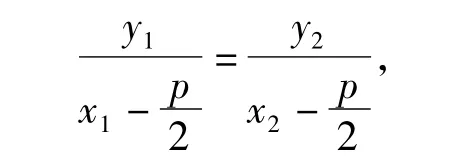
T：S6的解法具有通性，S7，S8的解法具有一定技巧，需要解题者有较强的洞察力.原题中|AF|，|BF|这2条线段值得关注，你能探索出这2条线段之间可能有什么关系吗?

S10：这个直角梯形的两底之和等于AB的长.

T：除此以外，还会想到什么样的结论?

S10：以AB为直径的圆与抛物线的准线相切.

T：你是怎样想到的?

S10：在初中曾证过类似的几何题.

T：好!你的发现实际上是抛物线过焦点的弦的又一条重要性质，请你说说证法.S10：如图3，取AB的中点M，过点M作抛物线准线l的垂线交l于点 M1，则

图3

因此以AB为直径的圆与抛物线y=2px(p＞0)的准线相切(教室里发出一片赞叹声).

教学感悟学生蕴藏着一种巨大的智慧潜能.只要教师对问题的思考达到一定的深度，让自己置身于学生之中，成为学生的合作者、“隐”导者、鼓励者，学生就能从特殊到一般、从直观到严谨，把新的认识上升到理性的、共性的高度，形成一般性结论.

3 变式探究，拓宽思维空间

一道以过抛物线焦点的弦为背景的习题可探究出多种解法和结论，如果把过焦点的弦变为过x轴上定点的弦，那么又会有什么结论?抛物线上的两点满足什么条件就能使这2个点连线经过抛物线焦点?这些问题同样值得探究.

变式1 如果将原题条件中的“焦点”改为“定点 C(c，0)(c＞0)”，其余不变，那么 y1y2的值还是定值吗?为什么?

有了对原题的探究基础，学生对这个问题的求解已不陌生，很快有学生陈述了自己的解法.

根据韦达定理，得直时，由点 A，B，C 共线得

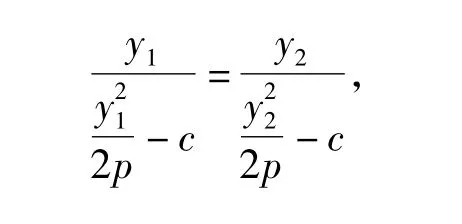
整理得

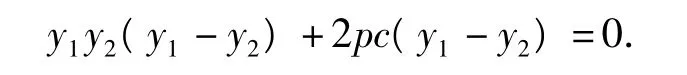
因为 y1≠y2，所以 y1y2=-2pc.

当AB⊥x轴时，方法同S11.

T：这2位同学的解法体现了一定的学习水平和研究水平，尤其是注意到了AB与x轴的关系，采用有效的方式来应对不同的情况，思路开阔、思维缜密.

变式2 如图4，设 A，B为抛物线y2=2px(p＞0)上2个点，C为抛物线准线上的一点，点 A，O，C 共线，且 BC∥x轴.证明：直线AB恒过定点.

T：要证明直线AB恒过定点，我们能否猜出这一定点.

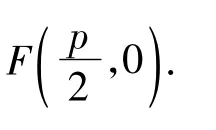
图4

T：你是怎么发现的?

S13：通过特例计算得到AB过抛物线的焦点.

T：很好!满足条件的直线AB恒过定点是一个具有一般性的结论，它必然包括特殊情况，S13用辨证的思想分析找到了目标.怎么证明，请把思路说一说.

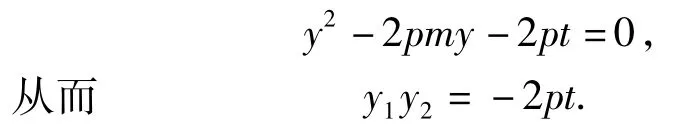
因此点A，O，C共线，且AC与x轴不垂直，于是则点M与点F重合，于是直线AB过定点F.

S14：设抛物线 y2=2px(p＞0)的焦点为 F，经过点F的直线交抛物线于点A，B，点C在抛物线的准线上，且BC∥x轴，证明：直线AC经过原点O(即证明点 A，O，C 共线).

S15：设抛物线 y2=2px(p＞0)的焦点为 F，经过点F的直线交抛物线于点A，B，延长AO到点C，交抛物线准线l于点C，证明：BC∥x轴.

T：S14，S15所编拟的2道题目与变式1是什么关系?结论成立吗?

S14：这2道题是变式2的逆命题，其证明的思路应该与变式2相仿.

T：应该相仿，看来你还不能肯定，可以试一试.

S16：我已证出S14的结论，证明方法与变式2确实相仿.

T：好，同学们的思维非常灵活，由一道题又变出了2道新题，这既训练了思维的灵活性，又使我们把握了这类问题的本质.同时，还告诉大家一个惊人的消息，S14所编拟的这道题就是2001年全国数学高考试卷中的解析几何题(同学们惊讶不已!顿时教室里响起了热烈的掌声).

教学感悟解题教学不能忙于“赶路”，弄透一题，胜于教完十题.只有走进题目的“心灵深处”，才能欣赏数学的“多彩世界”.

4 横向联系，提升综合能力

在不同的知识背景下，运用所学知识分析并解决问题是对学生学习能力的检验.因此，培养学生探索、提取、应用知识的能力，方能为问题的探究提供有力的智力保障.

如果把变式2以向量的形式呈现，那么可衍生出如下题目：

(1)当t变化时，求点B的轨迹n;

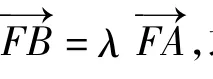
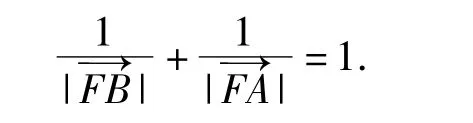
T：看到这道题目后，首先想到了什么?

T：你能说说求点B轨迹方程的思路吗?

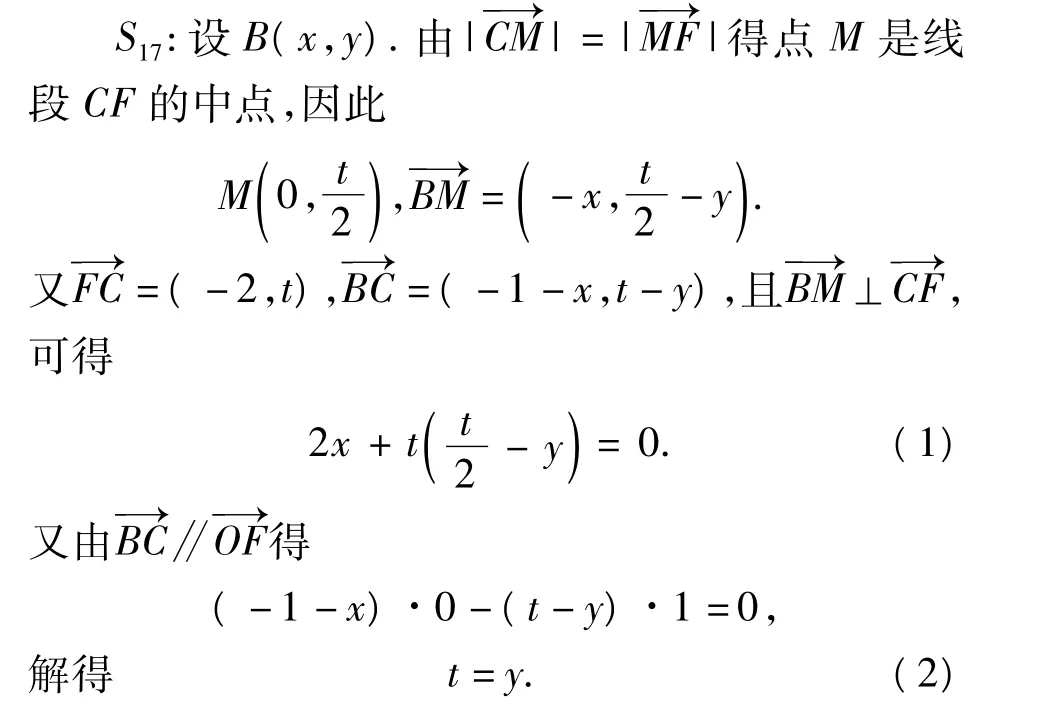
由式(1)，式(2)消去t得

所以点B的轨迹为以原点为顶点，焦点在x轴正半轴上的抛物线.

T：这是一道求动点轨迹的题目，而条件是通过向量形式表现出来的.如何实现向量条件的转化，是解决这道题目的关键.S16较好地把握了这一关键，值得大家学习.

教学感悟 将原题的条件换一种方式呈现，尤如让学生“在不同地方见到同一个人”，有利于知识的沟通，强化知识间的内在联系.

5 精选习题，有效开发资源

课本是教学之本、教学之源，同样课本也应成为课堂教学的探究之本、探究之源.课本上有许多适于探究的鲜活材料，作为教师必须以睿智的目光发现适于探究的素材，并进行有效开发.

5.1 选题要具有典型性

课本上的很多习题都具有一定的代表性，它的价值在于基础性和可探究性.只有选取这样的习题，才能构建基础性训练和探究性训练的思维体系，才能使探究活动有一个基本保障.离开了这个保障，探究活动就不能有效地开展下去;离开了这个保障，学生的学习兴趣和积极性就不能有效调动.因此，精心选题是保证全员参与的前提，也是保证整体教学效益的前提.

5.2 问题的设计要有层次性

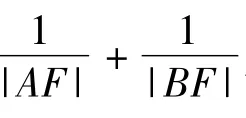
5.3 探究过程要注重学法指导