连云港港口货物吞吐量自适应过滤预测模型及其Excel宏实现
2010-08-21王继顺王传斌连云港师范高等专科学校江苏连云港222006WANGJishunWANGChuanbinLianyungangTeacherCollegeLianyungang222006China
王继顺,王传斌(连云港师范高等专科学校,江苏连云港222006)WANG Ji-shun,WANG Chuan-bin(Lianyungang Teacher's College,Lianyungang 222006,China)
连云港港口货物吞吐量自适应过滤预测模型及其Excel宏实现
Self-adaptive Filter Prediction M odel of Lianyungang Port Throughput and Realization w ith Excel Macro
王继顺,王传斌(连云港师范高等专科学校,江苏连云港222006)
WANG Ji-shun,WANG Chuan-bin(Lianyungang Teacher's College,Lianyungang 222006,China)
利用自适应过滤预测法对连云港港口2008年前几个月货物吞吐量数据建立港口吞吐量预测模型,通过VBA编程实现Excel的宏按钮操作,按照预测误差方差最小原则交互实现迭代功能,选择对最小预测误差方差贡献最小的一期对应的权值作为最佳权值进行预测,获得了精确度较高的预测结果。
港口货物吞吐量;自适应过滤法;预测模型;Excel宏;VBA编程
Abstract:By analyzing the modeling process of the self-adaptive filter prediction,the self-adaptive filter prediction model is introduced to predict the port throughput based on the data of Lianyungang port throughput from several earlier months in 2008.Programs are realized to the iterative function alternately according to the principle of the smallest variance of forecast error using excel macro and VBA codes.In the iterative procedure the weights are chose to take the best weight corresponding to a smallest issue among the smallest variance of forecast error will carry on the forecast,which results show that the method can effectively solve the port throughput prediction problem.
Key words:port throughput of goods;self-adaptive filter method;prediction model;Excel macro;VBA code
Self-adaptive Filter Prediction M odel of Lianyungang Port Throughput and Realization w ith Excel Macro
0 引言
以连云港为龙头的江苏沿海地区发展规划获得国务院批准以来,港城发展跃上国家战略平台。连云港从上到下正积极放大政策效应,组织动员全市结合实际,扎实推进规划实施。其中积极扶持连云港港口开展对外贸易,港口建设步伐越来越快。港口建设必须在科学的港口规划指导下进行,而港口规划的制定离不开对港口吞吐量的合理预测。港口货物吞吐量预测是港口总体规划的重要研究内容之一,预测结果的合理性和准确性对于港口的总体布局、建设规模以及集疏运等配套设施的建设具有重要的指导意义。
港口货物吞吐量是一个复杂变量,受到多方面因素的综合影响,各因素间存在着许多无法确定的变量和关系,在进行港口货物吞吐量预测时,一般采用时间序列预测、回归分析预测[1]、趋势法预测、分块组合预测[2-5]、线性灰色预测[6-7]等。这些方法都存在一定的局限性,各有其适用条件。为了减弱各类因素影响的累积效应,对于港口吞吐量的预测宜就近采用小样本数据。而自适应滤波法适用于对“数据点较少,约束条件较少”的问题进行分析预测,且简单易行,具有自适应性,它能自动调整回归系数,是一个可变系数的数据模型[8]。因此,港口货物吞吐量的预测问题可以采用自适应过滤模型来解决。
1 自适应过滤法原理及建模方法
1.1 自适应过滤法原理
自适应过滤法的基本原理就在于通过反复迭代调整加权系数,“过滤”掉预测误差,选择出“最佳”加权系数用于预测。整个计算过程从选取一组初始加权系数开始,然后计算得到预测值及预测误差,再根据给定公式调整加权系数以减少误差,经过多次反复迭代,直至选择出“最佳”加权系数。由于整个过程与通信工程中过滤传输噪声的过程极为接近,故被称为“自适应过滤法”。
设x1,x2,…,xl为某一时间序列,自适应过滤法就是从自回归系数的一组初始估计值开始,运用自适应过滤法调整权数的计算公式为[8]:

逐次迭代调整,以实现自回归系数的最优化。其中,φi、φ'i分别表示调整前后第i期的权数,k为调整系数,也称学习常数或滤波参数,et+1=xt+1-xˆt+1为第t+1期的预测误差,xt-i+1为第t-i+1期的观察值。然后将优化的系数代入时间序列的预测模型[8]:

式中,xˆt+1是第t+1期的预测值,xt-i+1和φi分别是第t-i+1期的观测值及当期的权数,p是模型阶数也即权数的个数。
1.2 自适应过滤法预测步骤
按照自适应过滤法的原理,应用该模型预测的基本步骤如下:
(1)首先确定模型阶数p及初始权数φi。在数据较少情况下,一般取p=2,而初始权数取为φ1=φ2=…=φp=1/p,有时也可以根据时间序列数据的自相关系数,利用Yule-Walker方程来求得。
(2)选择合适的滤波参数k。学习常数的选取直接影响权数调整的速度,在一定程度上还会影响最终的预测结果。按照式调整权数的自适应过滤法收敛的充分条件是[8]:

(3)计算每一次残差et+1=xt+1-xˆt+1。
(4)根据残差et+1以及调整公式(1),计算下一轮的系数。
(5)迭代直到取得合适的系数。
在迭代过程中,当预测误差降为0时,系数的调整过程即告结束。但大多数情况下,由于序列是随机的,最终的预测误差无法降到0,此时使用的衡量标准为均方误差:
当继续迭代MSE不再进一步改善时,即认为MSE达到最小,系数的调整过程结束。用这时的权数作为最佳权数来计算第n+1期的预测值。另外,若权数调整进行到第n期,这时循环迭代调整的计算已经使用了全部的原始数据,而MSE仍然没有达到最小值的要求,这时可以将最后得到的一组权数作为新的初始值,进行新一轮的迭代调整,直至满足MSE收敛于最小值为止。
1.3 应用自适应过滤法预测准则
应用自适应过滤法时还要注意下面的两个准则:
(1)自适应过滤法主要用于水平的数据,对于有线性趋势的数据,可以应用差分方法来消除数据的趋势。
(2)当数据的波动较大时,在调整权数之前,对原始数据值作标准化处理,可以加快调整速度,是权数迅速收敛于“最佳”的一组权数,并可使学习常数k的最佳值近似于1/p,从而使自适应过滤法更为有效。数据标准化公式为[8]:
即k值可以根据时间序列中p个最大值来确定,但为了提高模型逼近最佳权数的速度,k值必须满足k≤1/p。

2 模型在港口吞吐量预测中的应用
选取连云港市沿海2008年港口货物吞吐量1~10月共有9个相关数据[9]。该数据集不能构成大样本数据,如果按照统计规律,就不能形成吞吐量的预测基础,也就不能对今后连云港市沿海港口吞吐量进行预测。但根据自适应过滤法的特点,可以很好地实现依据小数据量对未来港口的发展趋势较为精确的预测。已知沿海港口吞吐量见表1。

表1 2008年连云港港口货物吞吐量单位:万吨
由表1可见,港口吞吐量随时间单调递增,按照自适应过滤法预测准则,首先运用Excel中的数据分析计算相关系数r=0.999873,数据高度线性相关,为此作差分处理,使数据变化规律呈现为水平特征,得到表2。

表2 2008年连云港港口货物吞吐量差分结果单位:万吨
表2中的差分数据基本变得水平,但其还具有一定的波动性,为下一步加快权数的调整速度,取模型阶数p=2,对数据运用公式(5)作标准化处理,结果如表3。

表3 2008年连云港港口货物吞吐量数据标准化
下面根据表3后三列的数据,进行权数迭代调整。为简单起见取初始权数φ1=φ2=0.5,由表3中x*t列数据按照公式(3)计算学习常数k≤0.9648,为使模型尽快逼近最佳权数,所以取k=0.5。进行迭代计算时为了便于操作,首先在Excel工作表中构造如表4的表格,在同一工作表中插入三个按钮:迭代计算、重复迭代和数据复制,利用Excel中的宏录制功能[10]录制相应的三个宏:Sub迭代计算(),Sub重复迭代()和Sub数据复制()。

表4 权数迭代调整计算过程及结果
在Visual Basic编辑器中将录制的宏代码改换成模型算法需要的程序代码,针对表4按照自适应过滤预测模型算法编写Sub迭代计算(),进行一步迭代后,由于数据不能实现循环选择性粘贴,所以在Sub重复迭代()模块中,将表4中t=7时得到的权数值φ'1t、φ'2t赋给t=3时的φ'1t、φ'2t作为初始权数进行新一轮迭代。为了获得最小的MSE及其对应的权数,或观察MSE的稳定情况,用Sub数据复制()将各步迭代的结果进行复制,它们的代码如下:


根据上述算法,经过初次迭代结果如表5,然后进行重复迭代4次,预测误差方差基本稳定在0.0219,数据不再有明显改进,且第一轮迭代预测误差方差最小。按照通常的做法即取φ1=0.4675、φ2=0.4687作为最佳权数进行预测,而现在取φ1=0.4796、φ20.4807作为最佳的权值,这是因为在最小误差方差中,该组权值所对应的误差平方对总的误差平方贡献最小。预测误差方差将每个预测值的误差以其误差的倍数放大,单个较大误差的预测值就能使误差的方差增加很多,因此,能使预测误差的方差最小的预测方法所产生的预测值一般不会产生某些个别的大误差,这样在保证误差平稳的基础上,选择一个误差平方对总的误差平方贡献最小的一组权值作为最佳权值,进行预测就可以提高预测的精度。实际上,通过对第9期和其他可预测各期的预测验证对比(如表6),利用该组权值的预测结果的误差较小。

表5 权数初次迭代调整计算结果
3 结束语
应用自适应过滤模型对连云港港口货物吞吐量进行预测,为解决复杂多变的港口货物吞吐量预测问题提供了有效的方法。该方法的优点能根据数据特点作差分处理和数据标准化,在权数调整迭代过程中,选择对最小预测误差方差贡献最小的一期对应的权值作为最佳权值进行预测,获得了精确度较高的预测结果。再就是利用Excel的宏语言VBA编写宏程序,用按钮操作简单易行,在精度调整的过程中,把反复迭代的调整结果拷到结果输出区域的下方,并再次进行迭代,得到下一次迭代调整结果,这样可以直观的对比调整前后的预测精度,取精度较高的作为预测模型,这是本程序的另一个突出的优点。但本预测模型完全是定量的,有一定的局限性,因此,港口职能管理部门在做计划、决策时,还可加入一定的定性分析,从而使得预测结果能更加切合实际。
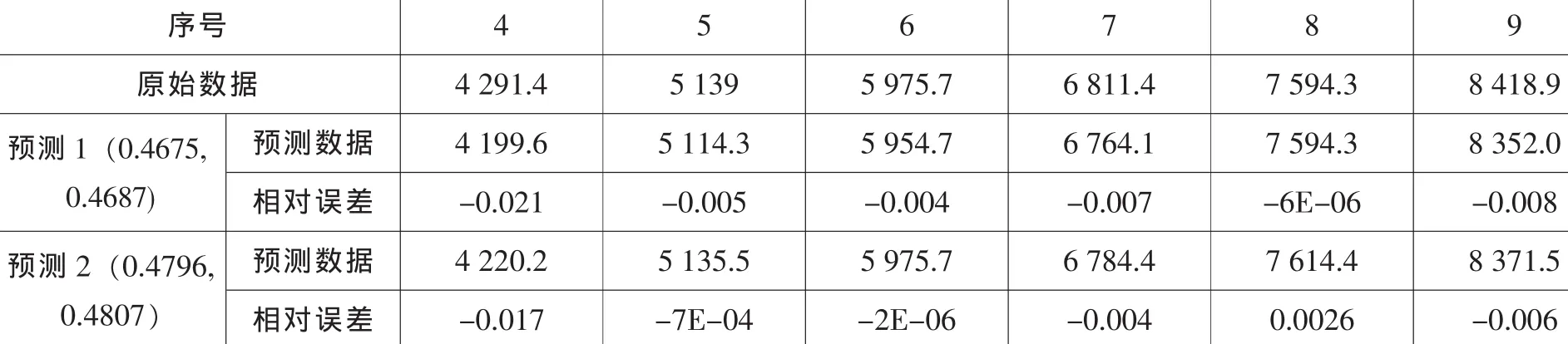
表6 预测验证与对比
[1]柴加龙,周起舞.回归与自回归的叠合模型在港口吞吐量预测中的应用[J].海洋通报,1995(3):93-98.
[2]张浩.基于最优线性组合的港口集装箱吞吐量预测方法[J].武汉理工大学学报(交通科学与工程版),2007,31(2):373-376.
[3]陈华友.基于相关系数的优性组合预测模型研究[J].系统工程学报,2006(6):353-360.
[4]张欣.组合预测模型在上海内河港口吞吐量预测中的应用[J].水运工程,2007(4):31-34.
[5]张云康,张晓宇.组合预测模型在宁波港集装箱吞吐量预测中的应用[J].中国水运,2008,8(1):33-34.
[6]许秀莉,罗键.GM 1,()1模型的改进方法及其应用[J].系统工程与电子技术,2002,24(4):61-63.
[7]刘燕,陈一梅.灰色系统模型在内河港口吞吐量预测中的应用[J].水运工程,2006(4):31-34.
[8]徐国祥.统计预测和决策[M].上海:上海财经大学出版社,2008.
[9]连云港市统计局.2008年1~10月主要经济指标[EB/OL].(2009-01-15)[2010-04-15].http://tjj.lyg.gov.cn/htm l/tjsj_ydsj/Index. htm l.
[10]Jelen.Excel 2007 VBA与宏完全剖析[M].北京:人民邮电出版社,2008.
U691
A
1002-3100(2010)10-0037-05
2010-05-19
连云港师专数学的应用与建模科技创新团队课题,编号:LSZTD200703。
王继顺(1970-),男,山东临沭人,连云港师范高等专科学校数学与应用数学系,副教授,硕士,研究方向:图论染色、数学建模及计算机辅助几何设计。
