重钢矿物码头通航二维水流数值模拟

2010-08-16房春艳孔德化

重庆交通大学学报(自然科学版) 2010年2期

房春艳，杨斌，朱旭，孔德化

(1.重庆交通大学河海学院，重庆400074;2.长江重庆航道局，重庆400010)

为积极响应重庆市“退市进郊、退二进三”的城市总体规划，解决长期制约重庆钢铁(集团)有限责任公司(以下简称重钢)发展的环境污染问题，经重庆市发展与改革委员会核准，重钢进行环保搬迁，根据集团公司要求和矿业有限公司的总体安排，新厂址选定在重庆市长寿区江南镇。重钢芭蕉角自备码头位于长江上游花朝门至汤家沱河段之间，长江北岸一侧。为了保证长江干线水道的畅通，避免因该工程的建设及施工作业导致长江白沙沱至大猫峡河段航道条件的恶化，以及给码头设计提供科学、合理的建设方案，需要对码头河段进行通航技术的论证［1］。

平面二维水流数学模型是目前分析河道水流流场的重要手段［2］。对于平面尺度远大于垂直尺度的水体，是一种在重力作用下的有自由面的水流。水体一般可视为不可压缩流体，属于牛顿流体范围，因此，对河道水流可作如下假设:水平速度沿水深方向取平均，建立平面二维水流数学模型。

1 平面二维水流数学模型

1.1 水流方程

采用沿水深平均的封闭浅水方程组描述二维水流运动［3］，基本控制方程见公式:

1)水流连续方程

3)y方向动量方程

上式中:t为时间;u、v分别为沿x、y方向的流速;h为水深;a 为床面高程;g 是重力加速度; εxx、εyy、εxy是紊动黏性系数;n为糙率系数。

1.2 边界条件

平面二维水流数模中，边界条件通常包括岸边界、进口边界、出口边界以及动边界等，本模型采用了如下边界条件［4］。

1.2.1 初始条件

对于给定的研究域，在时间t=0时有:

其中:h0、r0、s0分别为初始时刻的水位和流量分量［5］。

1.2.2 边界条件

1)开边界

其中:rB、sB分别为已知流量过程线;hB为已知水位过程线［6］。

2)固壁边界

即水与陆的边界，由壁面的不透水性，可令法向流速等于0，切向流速由曼宁－谢才公式确定。若法向流速与x轴夹角为θ，则r和s与vn和vt之转换关系为:

1.3 基本方程的数值离散与求解

采用拉普拉斯方程进行正交曲线坐标的转换。设(x，y)为物理平面上的笛卡尔坐标系，(ξ，η)为变换平面上的直角坐标系，它们满足拉普拉斯方程［7］:

求解此拉普拉斯方程，即可获得河道贴体正交坐标系下的计算网格［8］。在一个以(ξ，η)网格点为中心的控制体积中，方程可离散为:

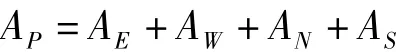
式中:E为前;W为后;N为上;S为下。

2 工程实例

该码头是重钢集团公司环保搬迁长寿统筹实施的必要的配套工程。拟建码头工程建设规模为1个2 000 t级散货泊位，泊位年吞吐量为100万t。根据流量、流向、船型和码头作业天数等基础，结合长江上游山区地形，并充分考虑本工程的特点进行码头和装卸工艺的研究，推荐码头采用架空直立墩式结构，该结构占据河道面积小，对河道流场影响较小。工程所在河段河势地形如图1。

图1 工程河段河势地形图Fig.1 Terrain of river regime on project reach

2.1 计算域的选取及网格的生成

根据工程所处位置以及工程后可能引起的洪水位影响范围，并考虑计算需要的进出口长度，选取计算区域为三溪子至鱼洞长江大处。计算域内共布置了500×50=25 000个网格点，网格线的交角除岸边个别节点以外均为88°～92°，基本保持正交。工程方案沿河流方向界于网格号210～214#之间，顺流向长约70 m，垂直流向宽约60 m，满足数模计算的要求。天然河道部分网格剖分如图2。

图2 工程河段网格Fig.2 Grid of project reach

2.2 模型验证

数学模型建立的正确性由模型验证这个环节来检验，只有获得了验证的模型，其计算成果的可靠性才得以保证。为此，本模型对工程河段的实测水面线、水流流速分布进行了验证。

2.2.1 验证所采用的资料

1)工程河段河床地形图(2007年测图，比例:1∶5 000);

2)不同流量下断面流速分布以及分流比资料(重庆交通大学珞磺护岸工程物理模型试验成果);

3)长江白沙沱河段实测枯水、中水水面线和断面流速分布(2006年、2008年)。

2.2.2 水位验证

根据实测中洪水水面线，进行了工程河段内各水尺断面水位验证。对平面二维数模的计算水位与实测水位的比较可以看出，二者符合程度较高，水面线走势吻合较好;另从水位验证的水位偏差值可见，偏差基本在±0.10 m之内，可见数模与实际情况吻合较好。从表1的水位偏差值可见，一般偏差均在±0.05 m内，最大偏差为±0.11 m。

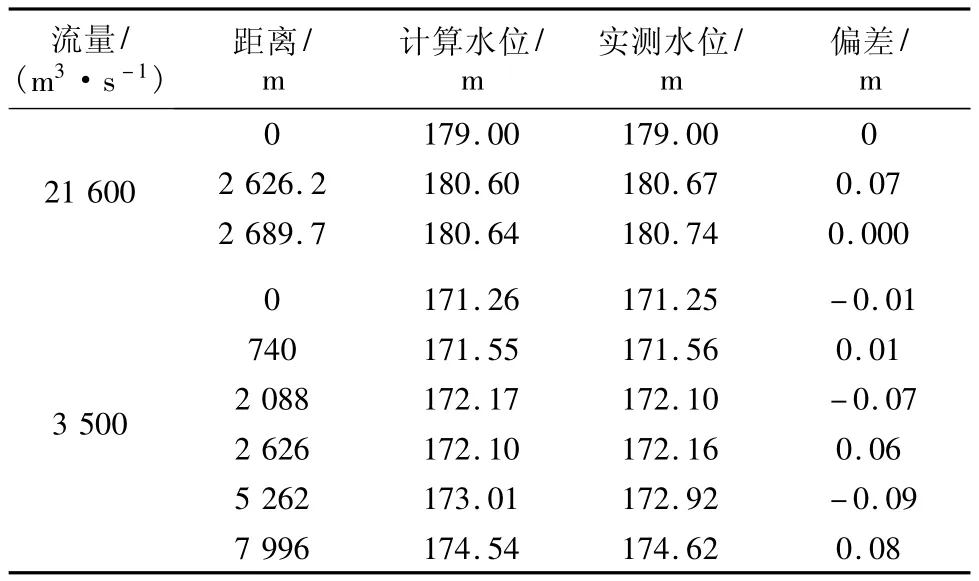
表1 水位验证表Tab.1 Verification of water level

2.2.3 流速验证

为了准确反映码头所在河段水流条件及船舶通航条件，于2008年7月对工程河段进行了河道地形和流速、流向、瞬时水位及船舶航迹线的测量(重庆航道局勘测处测量)，同时，应用建立的水流数学模型，对工程河段验证流量进行二维流场数值计算，经过对实测流速与数模计算流速进行对比。可见，流速的大小和分布以及最大值、最小值的位置均与实测资料较为一致。各测点流速的计算值与实测值之间的差值大多在±0.15 m/s内，个别差值较大的也在±0.25 m/s以内，偏差差不多在±10%以内。水流数模模拟的流速分布及其大小与实际水流基本吻合。

2.2.4 计算组合及工况

数模进行了代表枯、中、洪及大洪水共4级流量的计算，由于三峡成库后，枯水期通航条件有较大改善，同时长江水流顶托作用较弱时为通航条件的不利情况，所以从不利的角度仅计算了三峡成库前以及长江几乎不顶托的情况。

对于工程方案工况，因该河段已确定为工程实施位置，根据初步论证该工程是可行的。计算的具体水位－流量组合见表2。部分流量级下工程河段流场图见图3～图4。

表2 计算水位流量组合Tab.2 Calculation of stage－discharge combination

图3 7 300m3/s工程河段流场图Fig.3 7 300m3/s velocity field of project reach

图4 30 000 m3/s工程河段流场图Fig.4 30 000 m3/s velocity field of project reach

2.2.5 计算结果分析

在计算的各级水位下，工程的修建对河道流场特征、主流带位置及水动力轴线影响不大，主要对河道左岸的流速及流场分布产生一定影响。对近岸50 m处的流速增幅约为0.02～0.15 m/s;近岸100 m处的流速增幅0.02～0.12 m/s;主流带流速增幅约为0.02～0.07 m/s;船舶航线上的流速增幅约为0.01～0.06 m/s，工程对主流流速影响不大，最大约为0.02～0.05 m/s，从5级流量的航线流速变化统计来看，工程修建后船舶上下行航线上流速增幅约为0.02～0.03 m/s，说明码头工程的修建对河道船舶通航水流条件影响不大。

考虑到拟建码头采用架空直立墩式结构，工程结构阻水作用有限，仅会对码头附近河段的水流条件产生一定影响。计算河段流场分布显示，码头工程的修建对河道流场特征、主流带位置及水动力轴线影响不大，主要对河道左岸工程附近水域的流速及流场分布产生一定影响;河心水域河道流速及右岸附近河道流速变化不大。可以预测该工程建成后，除对工程附近泥沙冲淤变形、河床形态产生不大的影响外，将不会对工程河段的河床演变规律及河势造成较大影响。