混凝土在持续荷载下的强度
2010-08-16李鑫鑫
郑 丹,李鑫鑫
(1.重庆交通大学 河海学院,重庆400074;2.中国长江三峡工程总公司,湖北宜昌443002)
由于工作环境的差异,混凝土在真实条件下的性能和设计中采用的实验室试验结果不同。在室内混凝土静载强度试验中,从施加荷载到试件发生破坏约为1~2 min[1],但实际上大坝等混凝土结构设计寿命都很长,在使用期间要经受长期持续荷载的作用。研究发现,混凝土在长期持续荷载下的性能与短期荷载下有差异。因此,有必要研究混凝土在持续荷载下的破坏强度,为混凝土结构的耐久性设计和安全性评价提供参考。
现有研究表明,在低于抗压强度的持续荷载作用下,混凝土会发生破坏,荷载水平越高,破坏时间越短[2]。朱伯芳等[3]统计了混凝土持续荷载水平和破坏时间的关系,如表1。

表1 持续荷载水平和混凝土破坏时间关系Tab.1 Time table of sustained loading level and concrete failure
朱伯芳[3]认为,可以采用式(1)来表示持荷时间对混凝土强度的影响:
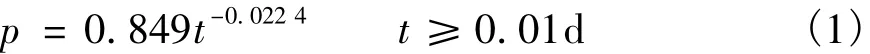
式中:t为持荷时间;p为持荷时间t下的强度与标准强度的比值。欧洲规范CEB-FIP(1990)[4]建议用一个系数βsus考虑长期荷载对混凝土强度的影响。
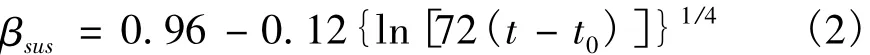
式中:t0为持续荷载开始作用时混凝土的龄期。
以上的表达式中只含有时间变量,而没有考虑混凝土长期性能密切相关的应力水平、材料组成、环境和构件尺寸等因素的影响,因而很难真正应用。
Iravan[5]和 Claeson[6]的研究表明,混凝土抗压强度越高,长期持荷强度与短期强度的比值越高。Neville[2]的研究表明,加荷龄期对混凝土的徐变破坏也有影响,施加荷载的龄期越长,长期持荷强度与短期强度的比值越高。彭凯等[7]认为混凝土单调加载全曲线是考虑徐变效应的应力-应变曲线的包络线,并在此基础上建立了混凝土抗压强度的徐变效应模型,但模型中未考虑在较高荷载下混凝土内的损伤。
可以看出,在长期持续荷载条件下,混凝土的强度和变形性能比较复杂,现有研究较少,不能较好地解释其破坏机理。笔者通过比较混凝土在持续荷载损伤与疲劳损伤的联系,分析了混凝土在持续荷载下的变形行为和损伤机理,研究了混凝土在持续荷载下的真实强度。
1 混凝土在持续荷载下的变形
大量试验表明,混凝土在持续荷载下会产生徐变等流变性能,其变形性能和应力水平关系密切。当应力较低时(图1),混凝土徐变和应力大小成正比。

图1 混凝土在较低持续荷载下的变形性能Fig.1 Concrete deformation under lower sustained loading
当应力水平较高时,混凝土徐变不再同应力大小成正比[2]。当荷载水平很高时(图2),混凝土的徐变和内部微裂纹的演化相互影响,导致混凝土经过一定时间的持续荷载作用即发生破坏[2]。
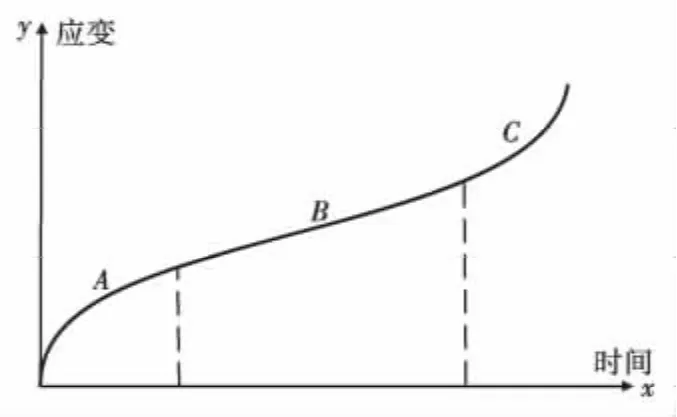
图2 混凝土在较高持续荷载下的变形性能Fig.2 Concrete deformation under higher sustained loading
由图2可以看出,混凝土在较高荷载下的非线性变形可以分为3个阶段:(A)线性徐变;(B)稳定的裂纹演化;(C)非稳定的裂纹扩展。在起初的2个阶段,损伤应变很小,在经过较长时间的第2阶段稳定变形后,由于混凝土内微裂纹相互作用,裂纹开始发生失稳扩展(第3阶段),混凝土变形迅速增大,导致材料发生破坏。
2 理论分析
根据现有理论和试验研究成果,可将混凝土在持续荷载下的应变表示为:
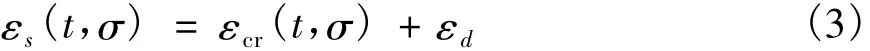
式中:εcr(t,σ)和εd分别为混凝土的徐变应变和损伤应变。
2.1 徐变应变
徐变应变可以表示为徐变系数和承受应力的乘积[2]:

式中:Φ(t)为徐变系数,与骨料、水灰比和加载龄期等有关。
Washa等[8]进行了荷载水平为1/4~1/3混凝土抗压强度,作用时间为10 a的试验研究,结果表明经过长期荷载的混凝土强度变化约为5%。因此,笔者认为混凝土的徐变不会对混凝土产生损伤,徐变应变是时间的函数;混凝土的损伤主要是内部的微裂纹演化引起的。
在较低荷载水平下,尽管混凝土的应变随着时间的增加持续增加,但由于其内微裂纹未发生扩展演化,因此并不发生破坏,并且长期持续荷载并不会明显削弱混凝土的强度;在较高荷载水平下,混凝土内微裂纹会发生扩展演化,导致混凝土内发生损伤,并且这个损伤与徐变变形相互作用,变形急剧增加,引起混凝土最终发生破坏。
2.2 损伤应变
研究表明,混凝土材料的非线性行为主要是由损伤演化(微孔洞和微裂缝的发展、融合和贯通等)和塑性流动来控制。在连续损伤力学的基本理论内,研究人员建立了一类基于能量的静力弹塑性损伤本构关系,可以用于各种情况下混凝土的典型非线性行为,在损伤力学的框架内,混凝土的应力-应变关系可以表示为[9]:
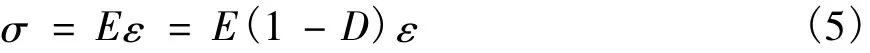
式中:σ,E,D,ε分别为应力、刚度、损伤变量和应变。
因此,混凝土在单轴受压情况下的应力-应变关系可以表示为:

式中:σ,E,D,ε分别为单轴荷载下混凝土的应力、弹性模量、损伤变量和应变。
由于混凝土在持续荷载下的损伤变形机理比较复杂,且现阶段缺乏系统全面的试验研究,因此笔者采用类比方法对此进行分析。现有研究表明,混凝土在持续荷载下和疲劳荷载下的变形性能非常相似,都经过了3个阶段,其中A为初始阶段,B为应变稳定发展阶段,C为应变失稳发展阶段,如图2。

表2 混凝土在疲劳荷载和持续荷载下不同阶段性能比较Tab.2 Performance comparison of concrete under fatigue loading and sustained loading at different stages
研究表明,在疲劳荷载下混凝土的破坏时间和第2阶段稳定疲劳的应变增长速率成反比,应变增长越快,破坏时间越短,反之亦然。Altenbach等[10]认为混凝土的疲劳损伤演化速率和应变率的幂成正比,如式(7):

式中:N为疲劳荷载周数;α,β为待定常数。
由于对混凝土的疲劳性能试验和理论研究较多,笔者借鉴疲劳损伤的模型来分析混凝土在持续荷载下的性能。根据混凝土在疲劳荷载和持续荷载下行为的相似性,可以认为在持续荷载下,混凝土的损伤演化率和损伤应变率的幂成正比:

式中:εd为损伤应变;T为持续荷载时间。对式(6)取微分可得:

根据式(8),可将式(9)转化为:
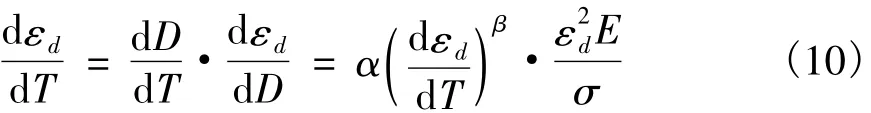
因此,持续荷载下混凝土的损伤应变率可表示为:

求解式(11)可得到混凝土在持续荷载下损伤应变的发展规律为:

2.3 破坏准则
在单调和循环荷载作用下,应力空间中存在着一个损伤状态相对应的包络面,这一包络面被称为边界面。混凝土在某一应力状态下的特性,都与这一边界面有关,应力点达到此边界面即达到了材料的强度[11]。根据边界面原理,混凝土的单轴应力应变关系全曲线的下降段即为混凝土在承受往复荷载时的应力-应变关系包络线(图3)。
根据细观分析,混凝土在持续荷载下的损伤变形时由内部微裂纹的损伤演化引起的,而混凝土的徐变是主要由基体的流变变形引起的。因此笔者认为,在一定应力的持续荷载下,当混凝土的损伤应变(而非总应变)超过应力-应变下降段所对应的应变时(临界损伤应变),混凝土即发生破坏,如图3。
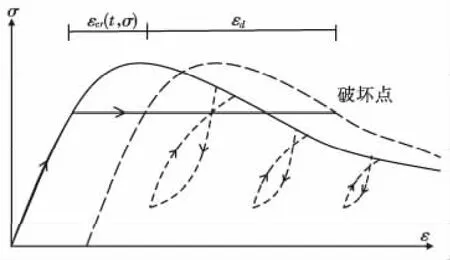
图3 混凝土在持续荷载下的变形至破坏过程Fig.3 The failure process of concrete deformation under sustained loading
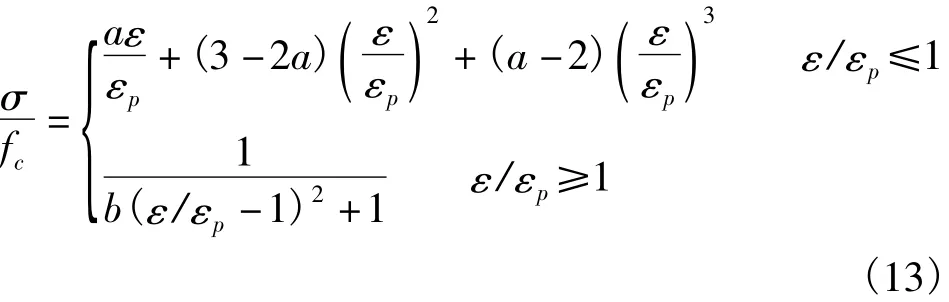
混凝土单轴受压应力-应变关系可以表示为[12]:式中:fc为混凝土单轴抗压强度;εp为混凝土单轴抗压的峰值应变,可用估算;a,b的数值可以采用式(14)估算[12]:
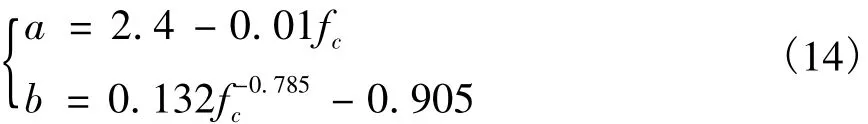
2.4 龄期对混凝土强度的影响
由于混凝土的水化过程持续时间很长,一般要几十年才能完成,因此在承受长期荷载的过程中,随着时间的增加,混凝土的强度也会随之增加,为考虑龄期对混凝土强度的影响,Washa[13]建议采用式(15)估算混凝土的强度随龄期的变化规律。
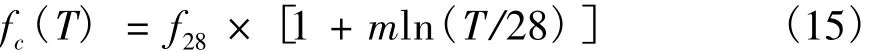
式中:fc(T)为龄期T时混凝土的强度;f28为混凝土28 d龄期的抗压强度;m与水泥品种、掺合物性质有关,对于普通硅酸盐水泥,m为0.173。
3 模型与试验结果对比
根据建立的模型,可以计算出不同荷载水平下混凝土的破坏时间。综合式(10)~式(15),可将不同荷载水平与破坏时间的关系用式(16)表示。
log10F(ε,T)=log10A+B0Plog10T (16)式中:F(ε,T)为龄期T混凝土的临界损伤应变。
根据表1的试验数据,可以直线拟合出A和B值,如图4。计算中混凝土的抗压强度取为30 MPa。
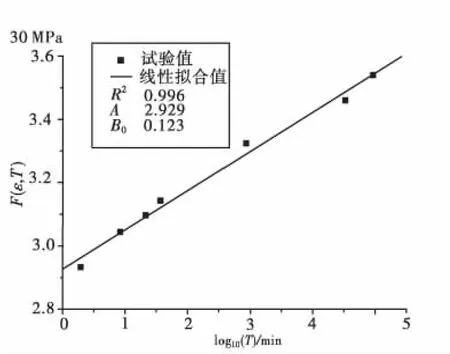
图4 试验数据拟合结果Fig.4 Fitting results of experimental data
在得到拟合参数后,可以由式(16)计算分析得到混凝土损伤应变以及临界损伤应变与持续荷载作用时间之间的关系,如图5。
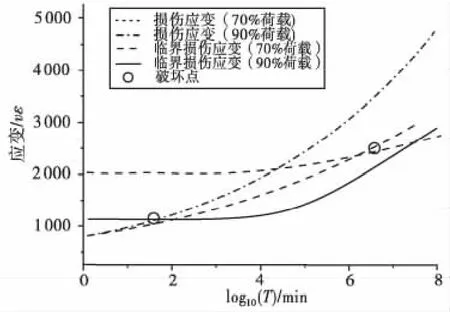
图5 混凝土损伤应变和临界损伤应变发展规律Fig.5 Development law of concrete under the damage and critical damage
由图5可以看出,随着持荷时间的增加,混凝土的损伤应变逐渐增大,与此同时,由于混凝土的强度随着龄期而增长,其临界损伤应变也随之增加,当损伤应变超过其临界值时,混凝土即会发生破坏。当荷载水平越高时,混凝土的损伤发展越快,并且临界损失应变较小,因此其破坏时间更短,反之亦然。
根据分析,式(16)计算得得临界损伤应变和式(15)代入式(13)中可以得出不同强度的混凝土(30、50 MPa)在不同持荷水平下的真实强度与持荷时间之间的关系,如图6。由图6可以看出,笔者提出的模型与现有试验结果吻合较好,可以较好地反映持续荷载水平和混凝土的破坏时间之间的关系。若以混凝土结构的设计工作时间50 a考虑,则混凝土在长期荷载的真实强度和短时荷载的比值约为72%(50 MPa)和68%(30 MPa),因此在混凝土结构设计中不能忽视。同时可以看出,随着强度增加,混凝土内部结构更为致密,其临界损伤应变增大,因此在持续荷载下的强度也较高,这与现有试验结论[5-6]吻合。

图6 混凝土强度与持荷时间的关系Fig.6 The relationship between concrete strength and loading time
5 结语
通过分析混凝土在持续荷载下的损伤变形机理和破坏准则,得到了不同强度混凝土在长期持续荷载下的强度与破坏时间的关系,可以得出以下结论:
1)混凝土在持续荷载下的破坏是由于混凝土的损伤应变随持荷时间逐渐增加而产生的,当损伤应变超过其临界值时,混凝土发生破坏。
2)当荷载水平越高时,混凝土的损伤发展越快,且临界损伤应变较小,因此其破坏时间较短。
3)持续荷载时间对混凝土强度的影响与混凝土的抗压强度直接相关,抗压强度越大,长期荷载强度与抗压强度的比值越高。
[1]DL/T 5150-2001水工混凝土试验规程[S].
[2][英]Neville A.Properties of Concrete[M].London:Pitman,1973.
[3]朱伯芳.论混凝土坝抗裂安全系数[J].水利水电技术,2005,36(7),33 -37.
[4][瑞士]CEB-FIP.Comité Euro-International du Béton[M].Switzerland:Lausanne,1993.
[5]Iravani S,MacGregor J G.Sustained load strength and short-term strain behavior of high-strength concrete[J].ACI Materials Journal,1998,95(5):636 -647.
[6]Claeson C,Gylltoft K.Slender concrete columns subjected to sustained and short-term eccentric loading[J].ACI Structural Journal,2000,97(1):45 -53.
[7]彭凯,黄志堂,肖盛燮,等.持续荷载下混凝土抗压强度的时效模型[J].重庆建筑大学学报,2004,26(4):29-34.
[8]Washa G E,Fluck P G.Effect of sustained loading on compressive strength and modulus of elasticity of concrete[J].Journal of ACI,1950,46(5):693 -700.
[9]余寿文,冯西桥.损伤力学[M].北京:清华大学出版社,1997.
[10]Altenbach H,Zolochevsky A.A generalized fatigue limit criterion and a unified theory of low-cycle fatigue damage[J].Blackwell Science,1996,19(10):1207 -1219.
[11]Suaris W,Ouyang C,Fernando V.Damage model for cyclic loading of concrete[J].Journal of Engineering Mechanics,1990,116(5):1020 -1035.
[12]过镇海.混凝土的强度和本构关系:原理与应用[M].北京:中国建筑工业出版社,2004.
[13]Washa G W,Saemann J C,Cramer S M.Fifty-year properties of concrete made in 1937[J].ACI Materials Journal,1989,86(4):367-371.
