混凝土翼裂纹损伤区与断裂区边界方程探讨

李 芮，向中富

(重庆交通大学土木建筑学院，重庆400074)

较多实验资料显示，混凝土在失稳断裂前，缝端存在着类似金属材料塑性区那样的微裂纹区。由于裂纹方位的不对称和荷载的不对称等原因，在混凝土结构中经常遇到复合型裂纹，因此复合型裂纹的断裂扩展研究有着更加重要的理论意义和实用价值。

用断裂与损伤耦合的方法来研究混凝土的破坏理论已成为固体力学研究的一个前沿课题。H.Horri和 S.Nemat-Nasser［1－2］及 M.F Ashby 和 S.D.Hallam［3］提出的滑动裂纹模型(sliding crack model)得到了不断的发展。滑动裂纹模型认为:当沿主裂纹的剪应力超过两裂纹面间的摩擦阻力时，裂纹面将发生滑动，从而导致主裂纹两端翼裂纹的萌生和发展;翼形裂纹将随着轴压力的增加而不断发展，逐渐趋于沿主压应力方向扩展。考虑到材料的复杂性，研究单条裂纹是远远不够的，需要考虑多裂纹相互作用的影响。近年来，许多学者都取得了很多有意义的成果。王元汉等［4］以斜裂纹和翼形裂纹为对象，分别介绍了压剪断裂和拉剪断裂的计算方法，以一个单向受压斜裂纹扩展过程，说明两种不同断裂型式的转换及计算模拟过程。孙雅珍等［5］应用损伤和断裂的耦合分析方法，研究了混凝土的破坏过程，确定初始损伤区域与断裂区，用损伤力学的方法数值模拟了3点弯曲混凝土梁的破坏过程。

笔者考虑断裂和损伤的耦合关系，建立了受压缩混凝土翼裂纹损伤区与断裂区边界方程，并给出单向受压混凝土损伤形状分布图，最后进行了实例计算，经过对比，本文研究结果与文献［4］相近。

1 混凝土的损伤本构关系

试验表明，混凝土在单轴压缩下的性能和损伤状况与单轴拉伸时有显著不同，损伤表现为各向异性。为了分析各向异性损伤模型，Sidoroff提出了能量等价原理，在能量等价原理的基础上，导出了受损材料的应力、应变和损伤能量释放率。Sidoroff提出损伤面的概念，得出各向异性损伤演化方程，令各向异性损伤演化方程中的损伤因子为相同的数值，转化为各向同性损伤模型，损伤因子为［6］:

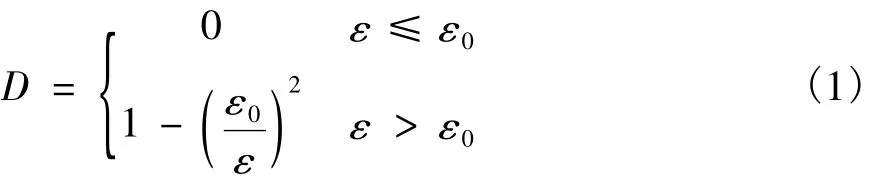
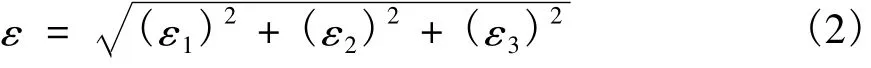
式中:ε1，ε2和ε3为3个方向上的主应变。

式(2)中当应变为负时，取值为0;即［x］定义为:

2 翼形裂纹损伤区与断裂区边界方程建立

式中:D为损伤因子;ε0为损伤发生时的应变;ε定义为:

在引入损伤以后，裂纹尖端将出现一个连续损伤的区域，裂纹的扩展是连续损伤的集中化发展引起的，在损伤区的外面才是无损区，裂纹扩展的过程就是裂纹尖端附近材料逐渐损伤引起的损伤区与断裂区移动的过程。

将混凝土梁简化成平面应力问题，设受压缩载荷作用后，梁中斜裂纹在两裂纹尖端都扩展了一定长度，形成了如图1的翼形裂纹。

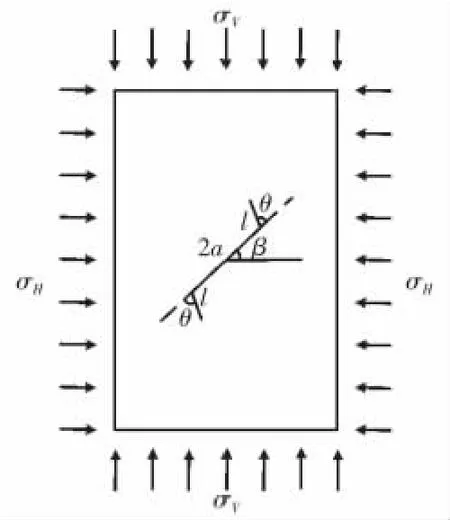
图1 受压缩载荷作用下的翼形裂纹板Fig.1 Plate with a wing crack under compression

设裂纹物体受垂直压力σV和水平压力σH的作用，主裂纹长为2 a，两端子裂纹长为l，它们之间夹角为θ。

对图 1 所示情形，Nemat-Nasser和 Horii［7］用复变函数方法计算过裂纹尖端的应力强度因子，后来又给出了其近似公式［8］:

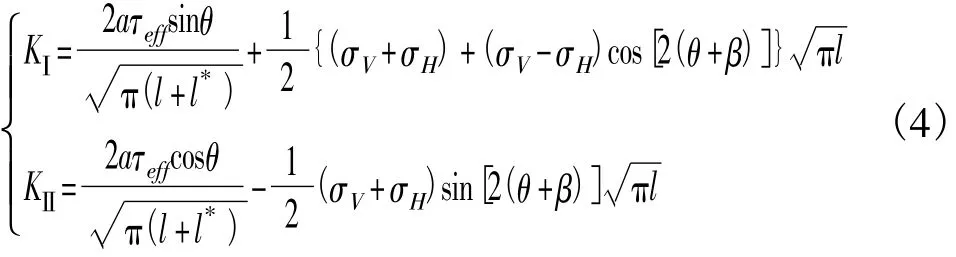
式中:l*是相对翼形裂纹的长度［2］，l*=0.27a;τeff表示主裂纹上的有效应力，且:

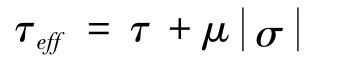
式中:τ和σ分别为主裂纹面上的剪应力和法向应力，如式(5):

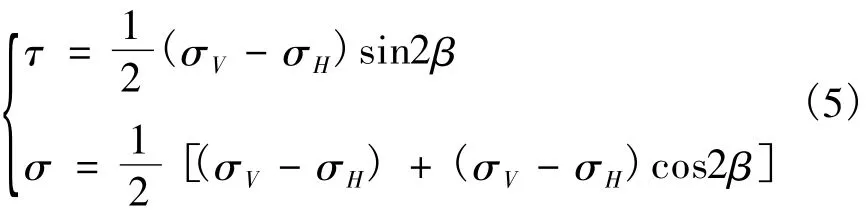
对图1所示的平面应力状态下ε3<0，取图2所示的裂纹尖端极坐标系，可推导出式(2)中定义的ε:

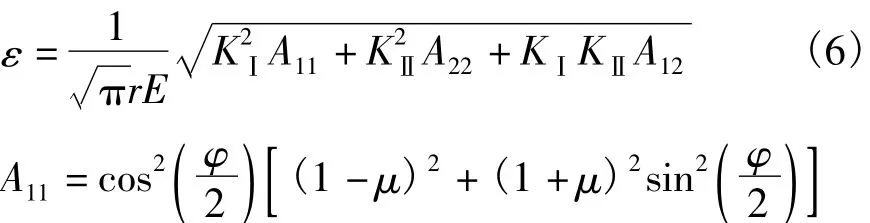
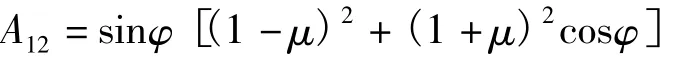
式中:E为杨氏模量;υ为泊松比。

将式(6)代入式(1)，得到翼型裂纹的损伤区和断裂区边界方程:

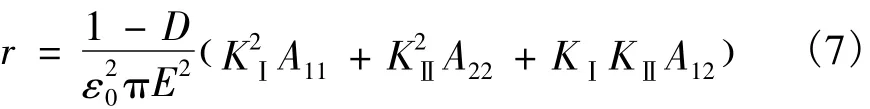
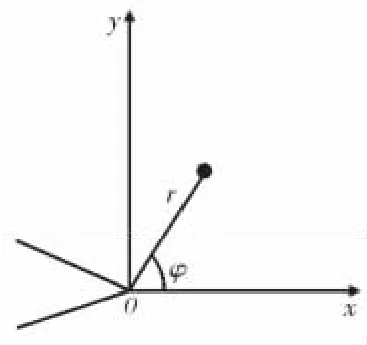
图2 裂纹尖端坐标系Fig.2 Coordinate system of crack tip

3 实例分析

3.1 单向受压的混凝土梁翼形裂纹

图3表示当σH=0时的混凝土梁受力示意图。

图3 单向受压的翼形裂纹板Fig.3 Plate with a wing crack under unidirectional compression

D=0为损伤区与无损区的边界，D=0.75为断裂区与无损区的边界。按照最大周向应力理论及其它实验结果，取断裂角φ01=70.5°。如图4所示，当子裂纹倾角φ01=70.5°时，画出斜裂纹不同倾角的损伤区形状。

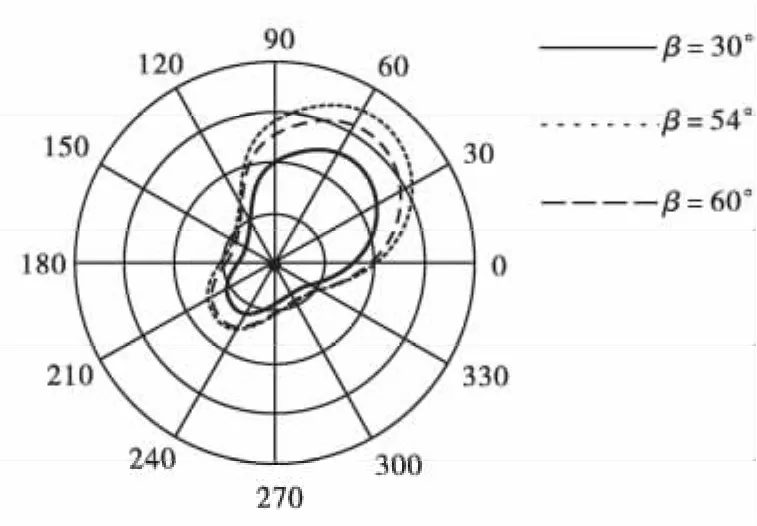
图4 不同倾角翼裂纹损伤区(D=0)的分布Fig.4 Distribution of damage zones due to wingcracks at different angles

以主裂纹倾角β=54°为例，画出翼裂纹尖端的损伤场，如图5。

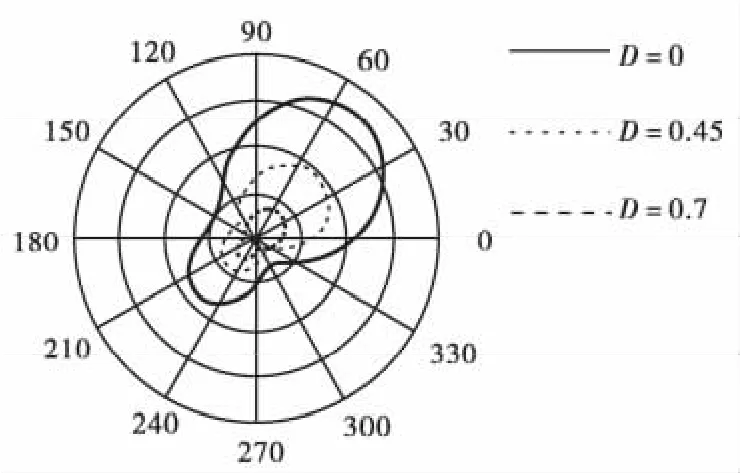
图5 β=54°时裂纹尖端损伤等值线分布Fig.5 Isoline distubution of damage zones near crack tips when β =54°

3.2 翼裂纹起裂点的坐标

为了说明本文的计算方法及过程，选用单向受压的翼裂纹混凝土试件作为算例。将表1中的几何及物理参数代入式(7)。

取第二次扩展的开裂角 φ02= －4.7°［4］，则计算得出:r=0.199 m。

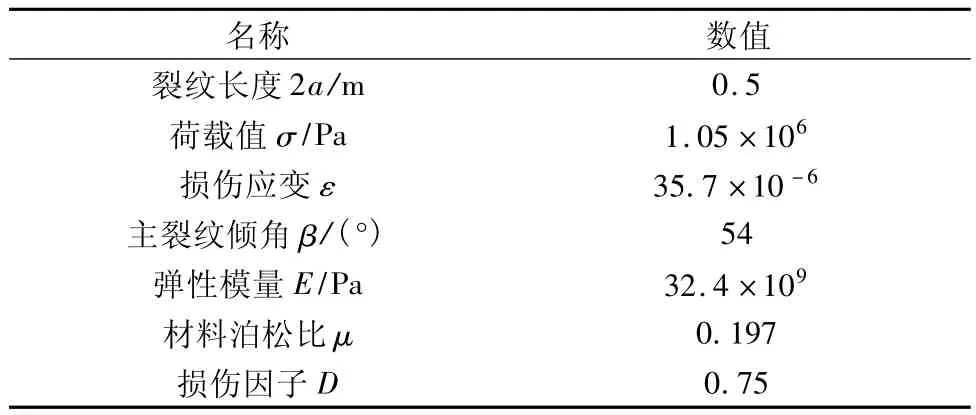
表1 混凝土试件的几何与物理参数Tab.1 The properties of the concrete specimen

所以当主裂纹倾角为54°时，混凝土试件翼形裂纹起裂点的坐标为(4.7°，199 mm)，这与文献［4］的结果接近。

4 结论

从以上分析可以得出:

1)混凝土在受压载荷作用下，由斜裂纹扩展成为翼形裂纹。笔者应用西多霍夫损伤模型和断裂力学耦合分析方法，以单向受压的翼形裂纹为例，探讨了翼形裂纹损伤区与断裂区的边界方程。

2)讨论并确定了混凝土翼形裂纹起裂点的坐标，通过与其它理论结果的比较，验证了本文方法的正确性。

3)按断裂损伤耦合理论，对混凝土单向受压翼形裂纹损伤与断裂区边界方程进行分析的初步尝试，同时为研究混凝土翼裂纹的扩展提供了一个新的思路。

［1］Horii H，Nemat N S.Compression-induced microcrack growth in brittle solids:axial splitting and shear-failure［J］.Journal of Geophysical Research，1985(90):3105－3125.

［2］Horii H，Nemat N S.Brittle failure in compression:splitting，faulting and brittle-ductile transition ［J］.Phil.Trans.R.Soc.Lond，1986，319(A):337 －374.

［3］Ashby M F，Hallam S D.The failure of brittle solids containing small cracks under compressive stress states［J］.Acta Metallurgica，1986(34):497 －510.

［4］王元汉，徐钺，谭国焕，等.岩体断裂的破坏机理与计算模拟［J］.岩石力学与工程学报，2000，19(4):449 －452.

［5］孙雅珍，余天庆.混凝土破坏的断裂与损伤耦合分析［J］.沈阳建筑大学学报:自然科学版，2006，22(1):53－56.

［6］Sidoroff F.Description of anisotropic damage application to elasticity［C］//Proceeding of IUTAM Colloquium on Physical Nonlinearities in Structure Analysis.Berlin:Springer-Verlag，1981:237－244.

［7］Horii H，Nemat N S.Compression-induced nonplanar crack extension with application to splitting，explosion and rock burst［J］.Journal of Geophysical Research，1982(87):6805 －6821.