大跨度钢桁拱桥节点疲劳性能试验研究
2010-08-11周志祥
周志祥,向 红,徐 勇
(重庆交通大学 土木建筑学院,重庆400074)
重庆朝天门长江大桥为公轨两用城市桥梁,主桥采用跨径布置为190m+552m+190m的中承式钢桁连续系杆拱桥(图1)。桥面采用双层布置,上层为双向6车道和两侧人行道,桥面总宽36.5m;下层中间为双线城市轨道交通,两侧各预留1个汽车车行道。下层桥面轨道横梁跨度达29m,通过连接角钢用高强螺栓与下弦节点的节点板相连。下弦节点直接承受公路荷载与轻轨荷载的双重作用,导致轨道纵梁与横梁连接部位的应力幅大,对于大跨度钢桁梁桥,节点疲劳破坏是其最主要的破坏形式[1-4]。目前常规钢桥节点的设计规范显得过于简单,并不适合大型复杂受力节点的静力承载能力分析,而关于大型节点的疲劳承载能力分析,设计规范更没有规定。由于重庆朝天门长江大桥轨道横梁与主桁连接在国内外大跨度钢桥中未曾有类似设计及试验,目前的疲劳研究还不够深入,系统的试验资料也较少,一些结构的疲劳性能理论分析只能作为参考,因此,节点连接部位的可靠性除了理论分析外,有必要对该种类型节点连接进行疲劳试验。
20世纪30-40年代,用小型的拉压试件,在能力为0~1 000 kN或±500 kN试验机上进行疲劳试验。试验的背景:一是焊接开始用于桥梁;二是发现铆接桥在多年使用后有疲劳开裂状况。美国从1967年开始进行大规模钢结构疲劳试验研究,提出了根据应力幅 Δσ和结构构造细节来确定疲劳寿命N的方法,该方法于1977年已为AASHTO公路桥梁设计规范[5]和AREA铁路桥梁钢结构规范所采用;日本钢结构协会疲劳设计指南[6]、英国BS5400[7]、欧洲钢结构规范[8]和西德桥规DN804也先后采用这些试验研究成果,该方法将不同的焊接接头型式,按疲劳强度相似情况分为 A、B、C、D、E、F 6个等级,分别给出了其容许应力幅[σ]与循环次数之间关系的容许应力曲线。由于材料、工艺、连接形式和构造细节的不同,上述国外研究成果与规范条文并不能照搬到中国大跨度钢桥节点高强螺栓连接的疲劳设计中,故只能提供参考。该文对照常规规范,根据朝天门大桥的交通量得出节点试验模型的试验荷载。采用空间有限元对全桥进行分析从而确定出全桥受力最不利的节点并完成从实桥节点到节点模型的转换,采用美国MTS公司的全自动液压伺服作动器进行200万次正常设计疲劳荷载试验,最后继续提荷载等级分逐级加载直到节点模型疲劳破坏。

图1 重庆朝天门长江大桥
试验提供的研究结果,一方面,通过对朝天门长江大桥这类高强螺栓连接节点的构造设计安全性和合理性的验证,从而对设计提出优化性建议,保证该类结构经济性和可靠性的实现;另一方面,可以为推动该类节点构造在大跨度钢桥中的应用,并为该类桥梁的设计及监测提供数据及参考意见。
1 疲劳试验荷载的确定
钢桥疲劳属于变幅、低应力、高循环、长寿命的疲劳范畴。但是,依照目前的实验设备、技术水平和试验研究周期要求,通常只能进行常幅疲劳试验,所以必须建立变幅疲劳强度和常幅疲劳强度(等效应力幅 Δσ0)之间的联系。所谓“等效应力幅 Δσ0”的概念是 :对于变幅应力循环 Δσi、ni(i=1、2、3……)的重复荷载作用,可以运用Miner[9-13]线性积伤律得到一个损伤度相同的常幅循环应力幅Δσ0,其循环次数为则称 Δσ0为“等效应力幅”。
构造细部的常幅疲劳曲线方程为:

由此可得该构造细部在 Δσi、ni(i=1 、2、3……)重复荷载作用下的损伤度为:
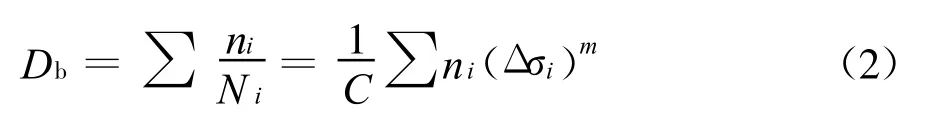
由式(1)可得该构造细部在“等效常幅 Δσ0”应力循环作用下的疲劳破坏次数N0为:


令:Db=D 0,则有:

于是等效应力幅为:

将朝天门大桥的营运荷载用标准疲劳车来代表,标准疲劳车出现的次数也根据与实际营运荷载等效的原则来确定。依据疲劳损伤累积理论的Miner线性积伤律,把标准疲劳车计算的内力幅值等效成200万次循环荷载的内力幅值,表1是根据英美规范计算的结果。

表1 根据规范计算的弯矩幅和剪力幅
从表中可以得出:节点连接处的等效弯矩幅应为:536.036 kN◦M、等效剪力幅应为:383.003 kN。
根据BS5400[7]规范对承受公路和铁路荷载的两用桥梁,为了得出总损伤度,应对2种损伤值的和再乘以一定的调整系数,以便把这2种荷载同时发生的概率考虑进去。根据实际情况调整系数一般不超过1.2,参考已有的研究成果[3-4],取调整系数为1.1。因此,对于重庆朝天门长江大桥,疲劳荷载循环200万次时,原型试验节点联结处调整后的等效弯矩幅为 589.64 kN◦M;等效剪力幅为 421.30 kN。最终确定疲劳试验荷载上限为213.5 kN,下限为103.65 kN,加载点距跨中5.2m处。
2 试验模型设计
为了解重庆朝天门大桥下层桥道的轨道横梁与下弦节点连接处的抗疲劳性能,模型在设计时尽可能地考虑实桥结构的受力特性及连接处的材质与构造细节:
1)用模型与原型的几何相似比为1∶2来模拟原型;
2)模型材质与实桥完全相同;
3)模型节点区域的构造细节与实桥一致;
4)模型与原型在考察重点区域受力性能一致;
5)模型的表面条件尽可能接近实桥结构。
通过满足这些条件使模型结构的应力状态、残余应力分布、应力集中情况、表面条件等尽可能接近实桥结构。实桥到模型的简化如图2所示,试验模型如图3所示。
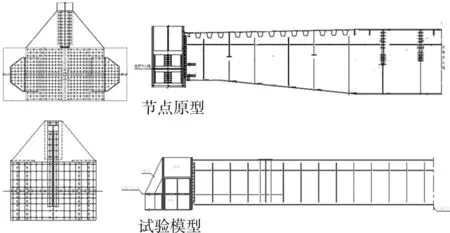
图2 实桥节点到节点模型的简化

图3 节点试验模型
3 试验模型应变测点布置
应变的测量采用电测法。根据试验模型的空间有限元计算分析结果选取有代表性的点进行应变测量,进而了解连接区域内的应力分布。下层桥道与下弦节点连接处受力复杂,因此在模型上该处3个区域全部布置3向45°应变花,通过监测其应变来测定模型的主应力、剪应力和Mises应力。在试验中对该区域及附近范围进行详细测量,布置较多测点,而对下层桥道与下弦节点连接处的其他部位只布置少量测点。图4所示为部分布置区域。

图4 节点板与连接角钢处应变片布置
4 试验结果
疲劳试验前首先进行预压静载试验,预压试验重复3次,疲劳试验过程中停机静载试验采用逐级加、卸载,每次静载试验重复3次,荷载分级为:


疲劳试验过程中,为了监测各测点应力,每加载 1 万 、2 万 、5 万 、10 万 、20 万 、40 万 、60 万 、80 万 、100 万 、120 万 、140 万 、160 万 、180 万 、200 万次后停机进行静载应变测量,以便通过测点应变变化,及早发现开裂或其它异常情况,应力变化情况如图5和图6所示。
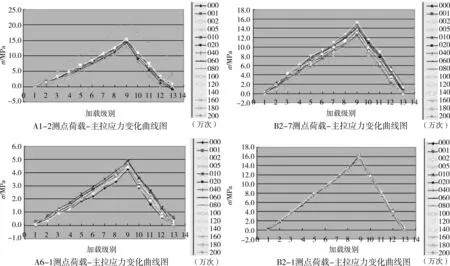
图5 节点板主拉应力实测值
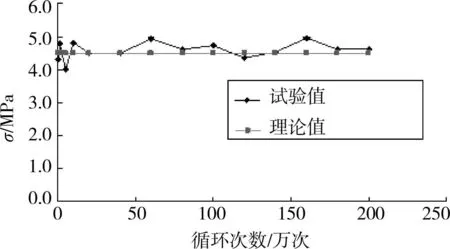
图6 B6-1测点主拉应力随循环次数的变化曲线图
纵梁与横梁交叉节点模型测点最大主拉应力为28.3mPa,出现在横梁上翼缘连接角钢上。模型测点的最大Von.Mises应力为57.3mPa,出现在梁腹板下部1/3处。横梁腹板与主桁节点连接角钢上测点的Von.Mises应力在60mPa以内。测点主拉应力在每次静载试验时,呈线性变化,各次静载试验的主拉应力数值差别不大,未发现测点应变有明显增大或减小现象。整个疲劳加载过程中未发现有异常现象。每次停机静载试验,检查试件,未发现裂纹,未发现螺栓有松动。200万次疲劳试验后,对试件进行检查,未发现裂纹,螺栓未发现有松动。
对试验模型建立了有限元计算模型(图7),计算结果见表2。从表1中可以看出,实测值与理论值的整体变化趋势基本上是相同的,除个别测点外,大多数测点都和理论值比较接近。在213 kN荷载作用下,除去轨道横梁加载截面附近外,模型测点的主拉应力理论计算最大值在30mPa左右,实测最大值在20mPa左右;Von.Mises应力理论计算最大值在55mPa左右,实测最大值在50mPa左右;通过理论分析和试验结果的比较,本次试验是成功的,试验的数据基本上反应了试件的工作状态,试验数据是可靠的。
5 疲劳可靠性评价
5.1 疲劳试验结果
从疲劳试验过程中的静载试验应力来看,绝大多数测点的主拉应力在20mPa以内,少数几个测点的主拉应力接近45mPa。实测拉应力远低于各构件的疲劳容许应力。另外,整个疲劳加载过程中未发现有异常现象,200万次疲劳试验后,对试件进行检查,未发现裂纹。下层桥道与下弦节点连接处的疲劳强度完全能够满足要求。
5.2 有限元计算结果
试验模型的应力水平不高,在213 kN荷载作用下,除去轨道横梁加载截面附近外,模型测点的主拉应力理论计算最大值在30mPa左右,Von.Mises应力理论计算最大值在55mPa左右 。从有限元计算结果来看,下层桥道与下弦节点连接处的疲劳强度完全能够满足要求。

图7 试验模型的有限元模型

表2 试验模型的应力实测值和理论值对比
5.3 相关规范验算结果
1)中国公路规范JTJ025-86[14]
ρ=0时,疲劳容许应力 [σn]=165mPa>45mPa,满足要求。
ρ=-1时,疲劳容许应力[σn]=103.13MPa>45mPa,满足要求。
2)铁路钢桥设计规范B10002.2-2005[15]
ρ=0.498,疲劳容许应力[σ0]=109.6MPa>45mPa,满足要求。
3)英国BS5400[7]
摩擦型高强螺栓连接的构造细节类型为C类,200万次疲劳强度50%保证概率下为161.9mPa,97.7%保证概率下为123.86mPa(其疲劳方程式为:lg N+3.5lgσ=13.63),满足要求。
4)美国AASHTO[5]
美国公路桥梁设计规范(AASH TO)中,细节分类B的常幅疲劳临界值为110mPa>45mPa,满足要求。从以上分析可以看出,重庆朝天门长江大桥下层桥道与下弦节点连接处的疲劳强度满足要求。
5)欧洲钢结构设计规范[8]
欧洲钢结构设计规范(EurocodE3 Part1.9)中,有关单边高强螺栓连接(细节类型 90),200万次97.7%保证率下的疲劳强度为90mPa>24.1mPa,满足要求。
6 节点模型疲劳破坏试验
在完成与设计寿命期对应的200万次疲劳循环加载试验后,对节点试验模型展开超长服役期内超负荷疲劳试验研究。具体试验破坏过程及现象描述见表3,图8是疲劳破坏后的腹板和角钢裂纹以及螺栓松动情况。
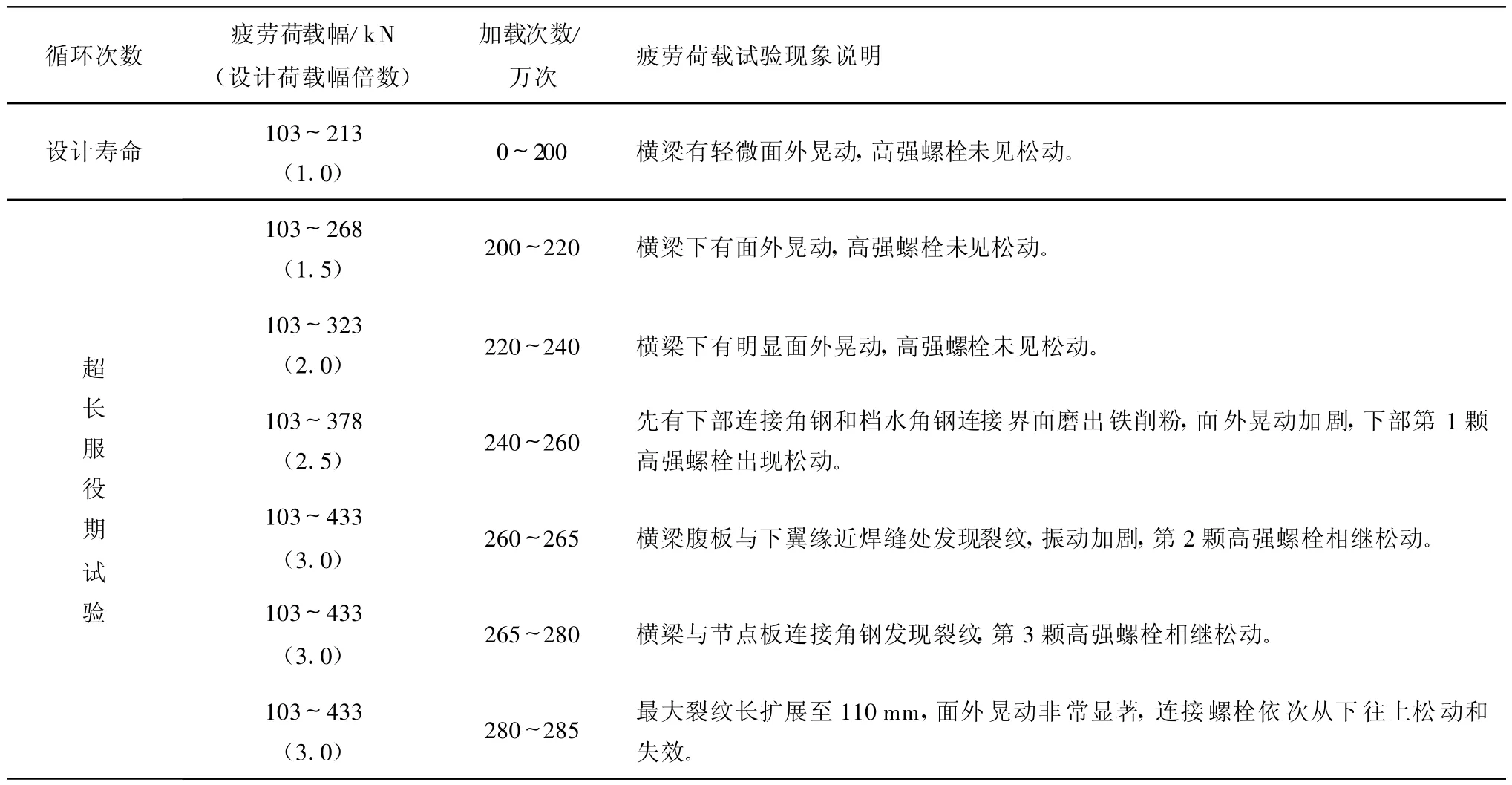
表3 节点从加载到疲劳破坏的过程描述
根据结构疲劳裂纹出现前,疲劳试验实测应力幅及加载循环次数,可以对结构疲劳寿命进行估计。根据公式[16]:

得出计算结果表明,在设计疲劳荷载幅作用下,试验模型中纵梁与横梁交叉节点连接结构的使用寿命(出现裂纹前)是其设计寿命的4.4倍。若将疲劳荷载幅提高1.5倍,试验模型中纵梁与横梁交叉节点连接结构使用寿命是设计寿命1.3倍。当疲劳荷载幅提高到2倍以上后模型开始出现破坏。

图8 疲劳破坏后的腹板和角钢裂纹
7 结论
1)200万次疲劳试验加载过程中,测点主拉应力呈线性变化,各次静载测试结果基本一致,节点处于弹性工作状态。
2)测点的动应变幅随循环次数变化不大,动应变波形曲线比较光滑,表明测点在疲劳加载过程中受力无异常。
3)200万次疲劳试验加载过程中未发现疲劳裂纹或螺栓松动等异常情况。
4)节点测区应力的理论值与实测值变化趋势一致,理论值稍大于实测值,理论计算能够把握节点实际工作状态。
5)模型试验和理论分析表明:M型节点连接构造在设计服役期内,在设计使用荷载作用下具有足够的抗疲劳强度。节点的估计使用寿命明显大于设计使用要求。
6)该节点疲劳破坏的历程归纳为:疲劳加载-振动-面外晃动-次应力产生-连接界面磨损-螺栓松动-联结性能退化-连接板件应力重分布-应力易集中部位出现疲劳裂纹。
[1]卫星,李俊,强士中.钢桁梁整体节点典型构造细节的抗疲劳性能分析[J].公路交通科技,2009,26(7):85-89.WEI XING,LI JUN,QIANG SHI-ZHONG.FatiguEperformancEof typical structurEdetail ofmonolithic Joints in Steel Trusses[J].Journal of Highway and Transportation Research and Development,2009.26(7).85-89.
[2]桂国庆,余长征,等.钢桥钢梁整体节点疲劳试验研究[J].工程力学,2001,18(4):38-44.GUI GUO-QIN,YU CHANG-ZHEN etc.experimental research on fatiguEof beam joints of steel bridges[J].Engineeringmechanics,2001,18(4):38-44.
[3]李俊,李小珍.轨道横梁与整体节点连接的疲劳试验[J].西南交通大学学报,2006,41(3):371-375.LI JUN,LI XIAO-ZHEN.FatiguEtest of connection between floor beams andmonohthic joints[J].Journal of Southwest Jiaotong University,2006,41(3):371-375.
[4]乔晋飞,李凤芹.钢桁结合梁整体节点及细节构造设计与研究[J].铁道工程学报,2009,131(8):68-81.QIAO JIN-FEI,LI FENG-QIN.Study and Design of integral joints and detailed structures of steel truss girder[J].Journal of Railway Engineering Society,2009,131(8):68-81.
[5]AASHTO LRFD.BridgEdesign specifications[S].3rd.ed.Association of StatEHighway and Transportation Officials,2004
[6]JapanesESociety of Steel Construction.FatiguEdesign recommendations for steel structures[R].1995,Technical Rep.No.32,Tokyo:JSSC,1995,(32).
[7]BS 5400-1980,Steel,ConcretEand CompositEBridges[S].
[8]prEN 1993-1-9 EurocodE3:Design of steel structures[S].FatiguEstrength of steel structures CEN TC/250/SC3 committeEdocument,2003.
[9]MINERm A.CumulativEdamagEin fatigue[J].J.Appl.Mech.1945(12):159-164.
[10]ZHANG W,MILLER kJ,A study of cumulativEfatiguEdamagEunder variablEloading-modEconditions[J].FatiguEFract Engngmater Struct,1996,19(2):229-239.
[11]周传月,郑红霞,罗慧强,等.MSC Fatigue疲劳分析应用与实例[M].北京:科学出版社,2005.
[12]FISHER J W,STRUIkS H A.GuidEto design criteria for bolted and riveted joints[J].John Wiley and Sons,New York:1987:266-283.
[13]惠纪庄,孙德仕,邹亚科.Miner线性累计损伤理论在汽车试验场可靠性试验强化系数研究中的应用[J].工程设计学报,2008,15(4):264-267.HUI JI-ZHUANG,SUN DE-SHI,ZOU YA-KE.Application ofminer linear cumulativEdamagElaw in reliability test intensifying coefficient on automotivEproving ground[J].Journal of Engineering Design,2008,15(4):264-267.
[14]中华人民共和国交通部标准.JTJ025-86公路桥涵钢结构及木结构设计规范[S].北京:人民交通出版社2002.
[15]中华人民共和国交通部标准.TB10002.2-2005铁路钢桥设计规范[S].北京:中国铁道出版社,2005.
[16]KULAkG L,FISHER J W,STRUIkJ H A.GuidEto design criteria for bolted and riveted joints[M].American InstitutEof Steel Construction, Inc.,Chicago,2001.
