CFRP约束混凝土圆柱轴心受压力学性能分析

梁 猛,董 伟,易富民,吴智敏

(大连理工大学海岸与近海工程国家重点实验室,辽宁大连116023)

近年来,纤维增强复合材料(简称FRP)因其高比强度、良好的耐腐蚀性和施工简便等优点已被广泛应用于既有混凝土结构的加固和修复工程中。其中,碳纤维材料(CFRP)是修复工程中常用的复合材料,而利用CFRP包裹混凝土柱以提高柱轴向承载力是较广泛的一种应用。

目前,已对CFRP约束混凝土柱轴压力学性能进行了大量的试验研究[1-9,11,17,22],也有学者基于Drucker-Prager模型(以下简称D-P模型)进行了数值分析[5-11]。采用D-P模型进行数值计算过程中,不同学者分别采用相关联流动法则和非相关联流动法则来描述混凝土的塑性流动状态。Yeh等[5-6]采用了基于相关联流动法则的D-P模型,但只考虑了CFRP环向包裹的情况。章文皇[7]、杨诗蔚[8]和杨婉倩[9]等也采用了相关联流动法则的D-P模型,从3位学者的数值计算结果来看,虽然混凝土柱的抗压强度计算值与各自的试验值差别不大,但轴向应变明显偏大,对混凝土柱的轴向变形情况模拟不够准确。Mirmiran等[10]和Sadeghian等[11]均基于非相关联流动法则的D-P模型,对CFRP约束混凝土柱轴压力学性能进行了数值计算,但在模型中将混凝土参数剪胀角均取为0,这与约束混凝土的膨胀特性有一定程度的不符,因为混凝土柱受不同厚度CFRP约束时的剪胀程度是不同的,剪胀角均取值为0说明不同约束程度却导致混凝土相同的剪胀性是不合理的。

采用非相关联流动法则来描述混凝土的塑性流动状态。根据塑性势理论,相关联流动法则认为混凝土的屈服面和塑性势面重合,而非相关联流动法则是把混凝土的屈服函数和塑性势函数分开考虑,认为混凝土的塑性流动不沿着加载面的法向方向。由塑性势理论和部分学者的数值研究工作[5-9]可知,应用相关联流动法则一般是出于数值计算简化的考虑,而非相关联流动法则能够更好地描述混凝土的受力和变形状态。为了更准确和全面地模拟CFRP约束混凝土圆柱的轴压力学性能,该文应用ABAQUS有限元软件中的混凝土扩展线性D-P模型[12]和非相关联流动法则,对CFRP约束混凝土圆柱进行了非线性有限元分析,并与试验结果[13]做了对比验证。在此基础上,基于该文建立的数值模型,讨论了外包CFRP厚度、缠绕角度和混凝土强度3种因素对CFRP约束混凝土圆柱轴压力学性能的影响。

1 材料本构模型

1.1 混凝土屈服准则(扩展线性D-P模型)

扩展线性D-P模型[12]在子午面上的屈服轨迹见1.2节中的图1,屈服准则表达式为

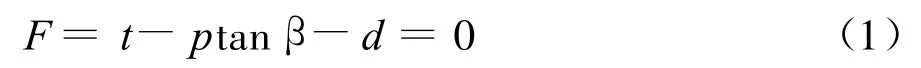
式中,p为等效压应力,p=-trace(σ)/3;β为线性屈服轨迹在p-t平面上的倾角,通常指材料的摩擦角;d为材料的粘聚力,其值与混凝土单轴压缩硬化参数 σc有关为偏应力参数,定义见式(2):

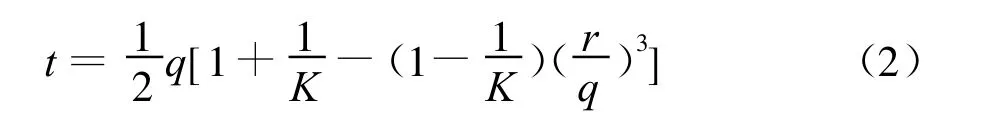
1.2 非相关联流动法则

在扩展线性D-P模型中,塑性流动势函数表达式为[12]

式中,ψ为p-t平面上的剪胀角。

为较准确地描述约束混凝土在多轴受力状态下的轴压受力性能,采用非相关联流动法则,则塑性应变增量矢量的方向与屈服面的法向方向不一致,即屈服面与塑性势面不重合,或屈服函数F与塑性势函数G不相等[24],在ABAQUS程序计算中表现为内摩擦角β不等于剪胀角ψ(2种角度取值详见3.1节),数学表达式见式(4),在p-t平面上的几何描述如图1所示。

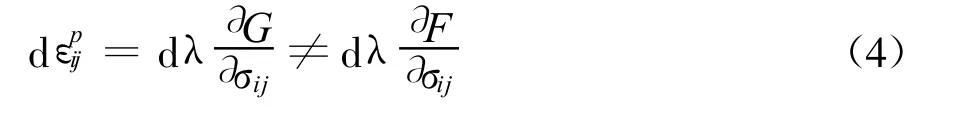
式中,dλ是一个非负的比例系数。

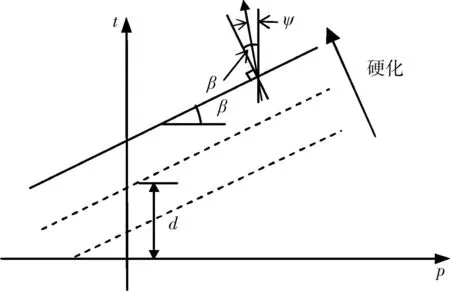
图1 线性D-P模型在p-t平面上强化和流动的几何描述

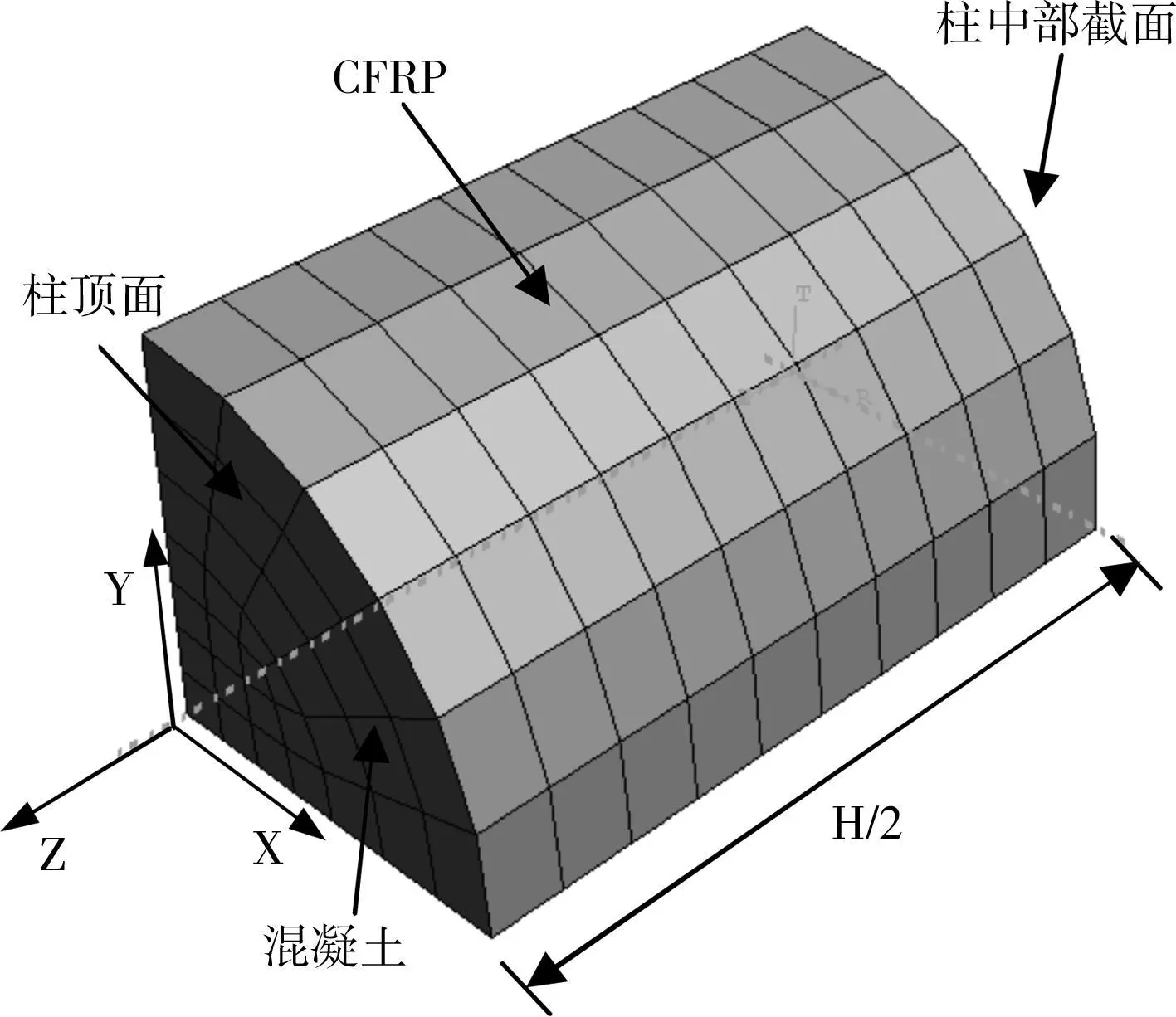
图2 有限元计算模型

1.3 CFRP的应力应变关系

该文采用的CFRP是单向纤维,为正交各向异性材料,沿纤维方向的应力-应变关系为线弹性关系。纤维方向和垂直纤维方向的弹性模量均取自文献[13]中的试验数据。

2 有限元模型

根据对称性,取圆柱的上部1/8柱体建立模型,如图2所示,在对称面上加载边界对称条件:YZ平面u=0,XZ平面v=0,柱中部截面w=0;柱的上表面XY面,在X和Y方向进行约束u=v=0,允许Z方向位移自由。将柱上表面所有节点设置成一个集合统一加载,加载方式采用位移控制。

为了更准确地模拟CFRP的平面受力的状态,CFRP采用 4节点减缩积分的四边形膜单元(M3D4R)。混凝土采用8节点减缩积分的六面体一次单元(C3D8R)。假设混凝土和CFRP之间粘结良好[14-15],程序中使用 tie命令将混凝土单元和CFRP单元的节点整合。

3 数值算例验证

3.1 算例模型

采用上述建立的有限元模型,对文献[13]中关于CFRP约束混凝土圆柱轴压力学性能研究的试验结果进行数值验证。计算中采用的混凝土圆柱尺寸为152.5mm×305mm(直径D×柱高H),圆柱体抗压强度 f′c为 19.4mPa,外包CFRP的弹模Ecfrp为82.7 GPa,极限拉应变εcfrp为0.027 5。由于圆柱外包的CFRP处于弯曲状态,且沿柱环向和轴向同时承受荷载,CFRP的环向极限拉应变比单轴受拉时有所降低,所以需要对CFRP极限拉应变进行折减,根据Teng等[16-17]的研究结果,CFRP的极限拉应变可取为0.586εcfrp=0.0161。数值分析中,将上述折减后的CFRP极限拉应变作为计算的结束点。

ABAQUS有限元计算中用到内摩擦角β和剪胀角ψ2个混凝土参数。关于内摩擦角β和剪胀角ψ的取值该文采用Eid等[18-19]建议的公式:

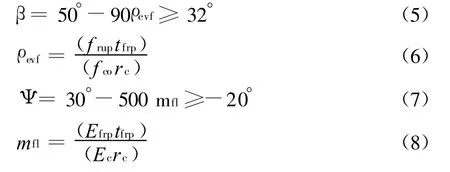
式中,ρevf和mfl分别为CFRP约束混凝土柱的侧向约束比和侧向刚度比,tfrp、Efrp和 frup分别为CFRP的厚度、弹模和极限拉应力,rc、Ec和fco分别为混凝土圆柱的半径、弹模和未约束混凝土的抗压强度。

由式(5)—(8)可以看出,内摩擦角β和剪胀角ψ均与混凝土受到的约束强弱有关,式(7)和(8)说明混凝土的塑性流动能力随约束的增强而减弱。通过式(5)—(8)的计算可得:当CFRP层数为1～5层时,该文的混凝土内摩擦角 β均取 32°,剪胀角 ψ随CFRP层数增加分别取 18°、10.5°、3°、-4°和-11.5°。

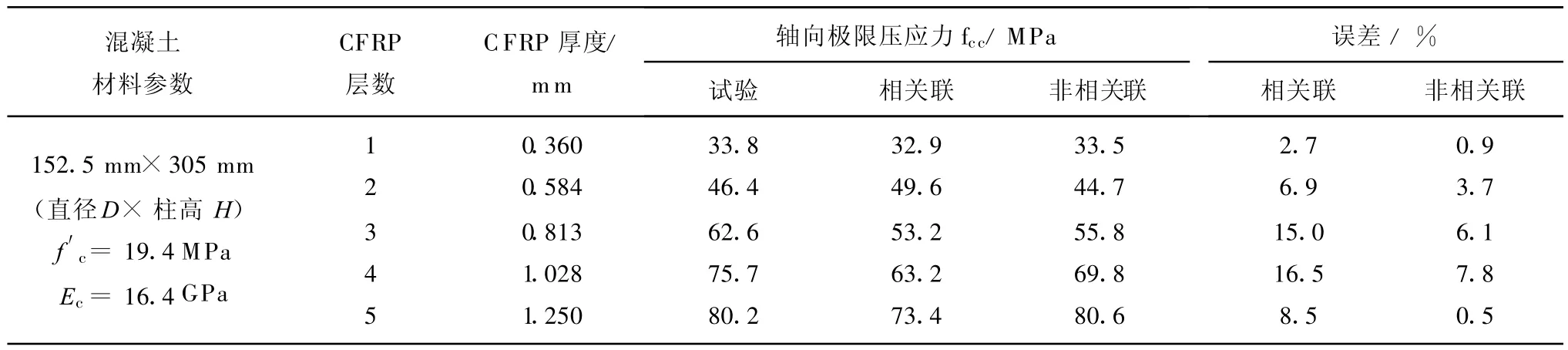
表1 材料参数和柱轴向极限压应力计算结果

3.2 计算结果与分析

CFRP约束混凝土圆柱数值计算结果与试验结果对比见表1和表2。由表1可知,采用相关联和非相关联流动法则计算得出的柱轴向极限压应力,对于不同层数CFRP的约束柱,计算值与试验值比较得到的误差(以下简称误差)最大分别为16.5%和7.8%。由表2可见,采用非相关联流动法则计算的柱轴向极限压应变,误差最大为11.9%,而相关联流动法则的误差范围在40%～70%之间。显然,采用非相关联流动法则计算得到的圆柱轴向极限压应力和压应变更接近试验值,计算的结果更准确。

图3为混凝土圆柱外包n=1～5层CFRP的有限元计算与试验得到的轴向和侧向应力-应变关系曲线,其中有限元计算采用了相关联和非相关联两种流动法则(图3中分别简称为“关联”和“非关联”)。虽然由相关联和非相关联流动法则分别计算的侧向极限应变比试验结果略大,但由非相关联流动法则计算得到的轴向极限应力和应变与试验值吻合得更好。因此,该文采用的基于非联合流动法则的扩展线性D-P模型可以较好地模拟CFRP约束混凝土圆柱的轴心受压性能。

表2 材料参数和柱轴向极限压应变计算结果

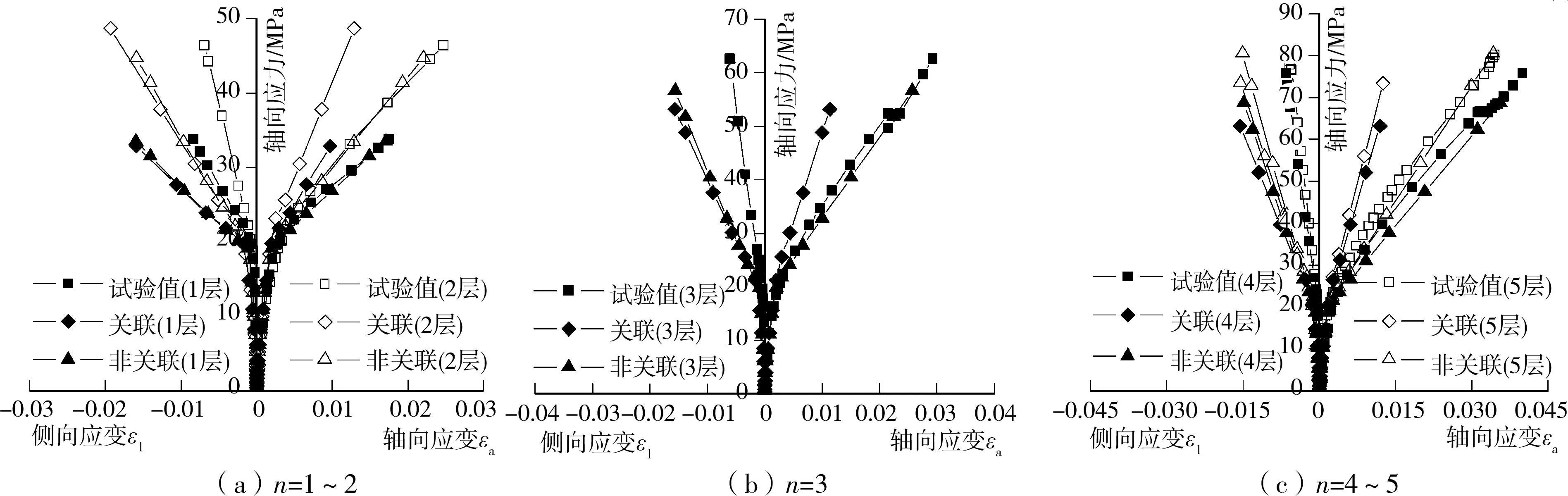
图3 外包n=1～5层CFRP柱应力-应变曲线

4 约束混凝土参数研究

采用扩展线性D-P模型和非相关联流动法则,分析CFRP厚度、CFRP缠绕角度和混凝土强度等3种因素对柱轴压力学性能的影响。其中,混凝土圆柱尺寸及各种材料参数与3.1节相同。

4.1 CFRP厚度

采用CFRP的层数分别取1～5层,不同层的厚度见表1,环向包裹,数值模拟结果见图4。由图4可知,随CFRP层数的增加,圆柱的轴向极限应力和应变均提高,而侧向极限应变变化不大。

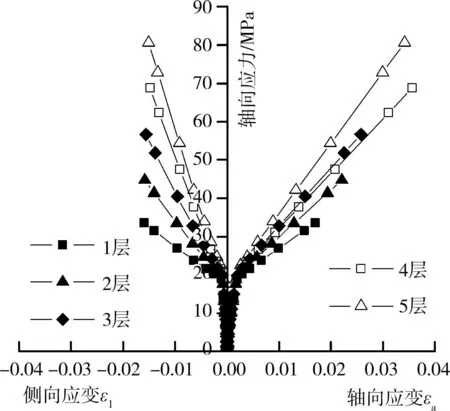
图4 外包n=1～5层CFRP柱应力应变曲线计算结果

4.2 CFRP缠绕角度

关于CFRP缠绕角度对混凝土圆柱轴压力学性能的影响,Parvin等[20-21]采用基于Mohr-Coulomb破坏准则的有限元方法研究了玻璃纤维(GFRP)不同缠绕角度对混凝土柱轴压力学性能的影响,但Parvin等[20]仅研究了0°和45°2种缠绕角度,Parvin等[21]仅研究了 0°和 15°2种缠绕角度。Sadeghian等[22]用试验方法研究了碳纤维(CFRP)不同角度缠绕的影响,试验中取了 0°、45°和 90°3种角度。该文采用混凝土扩展线性D-P屈服准则和非相关联流动法则研究了碳纤维(CFRP)不同缠绕方向对C20混凝土圆柱轴压力学性能的影响。其中,包裹CFRP均为2 层,CFRP缠绕方向为 0°/0°、15°/-15°、30°/-30°和 45°/-45°4种方向。由图5 可知,环向(0°/0°)缠绕CFRP柱的极限压应力最大,而45°/-45°方向缠绕柱的极限压应变最大,即延性最好。

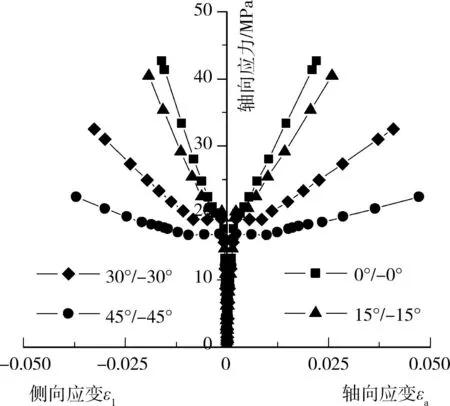
图5 CFRP不同方向缠绕柱应力应变关系

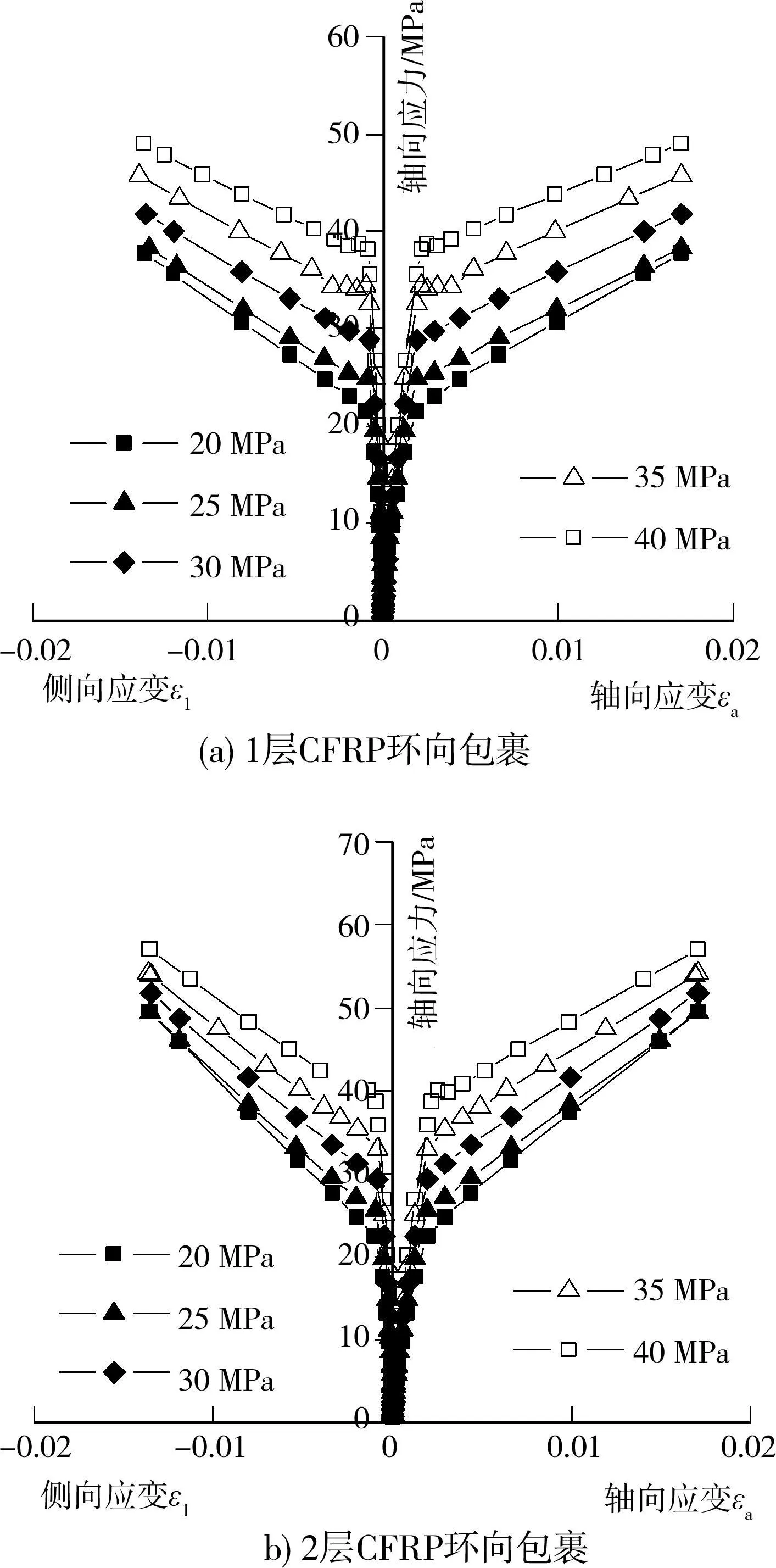
图6 1层和2层CFRP约束 f′c=20～40mPa混凝土柱的应力应变关系

4.3 混凝土强度

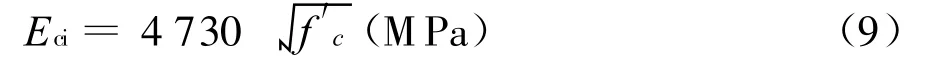
受压混凝土本构关系采用Carreira和Chu[23]的计算模型,表达式如下:

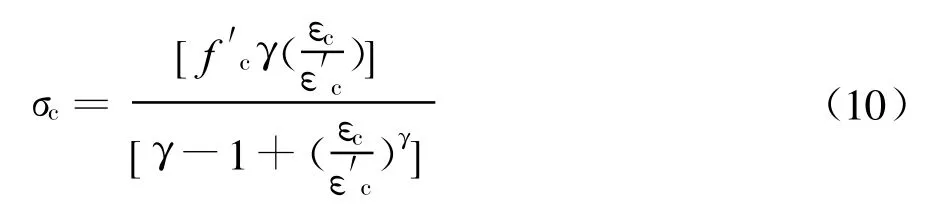
式中,γ是与初始弹模 Eci有关的函数,γ=为峰值应力时的应变 。

混凝土柱外包的复合材料为CFRP,其材料参数与3.1节相同,层数为1层和2层,均为环向缠绕,模拟得到的应力-应变关系如图6所示。由图可知,侧向约束相同的情况下,柱的应力-应变曲线第2段的斜率随混凝土强度的增加而减小,即混凝土强度越低,CFRP约束混凝土柱的极限应力和应变提高的程度越高,柱刚度提高的程度越大。

5 结论

基于非相关联塑性流动法则的混凝土扩展线性D-P模型,对CFRP约束混凝土圆柱的轴压受力性能进行了非线性有限元分析,并与试验结果进行对比验证,可得出以下结论:

1)由非相关联流动法则计算得到的结果与试验结果吻合良好。因此,采用非相关联流动法则可较准确地分析CFRP约束混凝土圆柱的轴心受压力学性能。

2)随CFRP厚度增加,混凝土圆柱的轴向极限应力和应变均增大,延性得到很大改善,而侧向极限应变变化不大。

3)CFRP成角度缠绕对柱轴压力学性能有影响,环向(0°/0°)缠绕 CFRP柱的极限压应力最大,而45°/-45°方向缠绕柱的极限压应力最小,但极限压应变最大,即延性最好。

4)侧向约束相同的情况下,随混凝土强度降低,CFRP约束效率反而提高,即CFRP约束混凝土柱的极限应力和应变提高的程度增加。

[1]TOUTANJI H.Stress-strain characteristics of concretEcolumns externally confined with advanced fiber compositEsheets[J].ACImaterials Journal,1999,96(3):397-404.

[2]XIAO Y,WU H.CompressivEbehavior of concretEconfined by carbon fiber compositEjackets[J].Journal ofm aterials in Civil Engineering,2000,12(2):139-146.

[3]滕锦光,陈建飞,ST史密斯,等.FRP加固混凝土结构[M].北京:中国建筑工业出版社,2005.

[4]岳清瑞,杨勇新.复合材料在建筑加固、修复中的应用[M].北京:化学工业出版社,2006.

[5]YEH F Y,CHANG kC.Confinement efficiency and sizEeffect of FRPconfined circular concretEcolumns[J].Structural Engineering andmechanics,2007,26(2):1-24.

[6]叶芳耀.碳纤围束混凝土柱轴压强度与极限应变之影响因子研究[D].台北:国立台湾大学土木工程学研究所,2004.

[7]章文皇.钢筋混凝土三轴拱围束效应用于补强柱受轴向及挠曲变形之探讨[D].台北:国立中央大学土木工程学研究所,2004.

[8]杨诗蔚.碳纤加劲复合材料管补强混凝土柱受轴压之非线性分析[D].台北:国立成功大学土木工程学研究所,2007.

[9]杨婉倩.复合材料围束混凝土柱受轴压之非线性行为分析[D].台北:国立成功大学土木工程学研究所,2008.

[10]MIRMIRAN A,ZAGERSK,YUAN W Q.Nonlinear finitEelementmodeling of concretEconfined by fiber composites[J].FinitEElements in Analysis and Design,2000 35(1):79-96.

[11]SADEGHIAN P,RAHAI A R.Numericalmodeling of concretEcylinders confined with CFRPcomposites[J].Journal of Reinforced Plastics and Composites,2008,27(12):1309-1321.

[12]ABAQUS,ABAQUS/Standard User'smanual[M].ABAQUS Inc;2003.

[13]SHAHAWYm,MIRMIRAN A,BEITELMAN T.Tests andmodeling of carbon-wrapped concretEcolumns[J].Composites Part B:Engineering,2000,31(6/7):471-480.

[14]代兵,侯景军.外包纤维布加固混凝土轴心受压柱力学性能分析[J].工业建筑,2006,36(S):1028-1031.DAI BING,HOU JING-JUN.ThEanalysis ofmechanics performancEof strengthened concretEcolumns wrapped with FRPunder axial compression[J].Industrial Construction, 2006, 36(S):1028-1031.

[15]黄艳,亓路宽.FRP布约束混凝土圆柱轴心受压性能非线性有限元分析[J].中国铁道科学,2008,29(1):46-50.HUANG YAN,QI LU-KUAN.Nonlinear FEM analysis of circular concretEcolumn confined with FRPunder axial compression[J].China Railway Science,2008,29(1):46-50.

[16]LAM L,TENG J G.Design-oriented stress-strainmodel for FRP-confined concrete[J].Construction and Buildingmaterials,2003,17(6/7):471-489.

[17]LAM L,TENG J G.UltimatEcondition of fiber reinforced polymer-confined concrete[J].Journal of Composites for Construction,2004,8(6):539-548.

[18]EID R,PAULTREP.Plasticity-basedmodel for circular columns confined with fiber-compositEsheets[J].Engineering Structures,2007, 29(12):3301-3311.

[19]EID R,DANCYGIER A N,PAULTREP.Elastoplastic confinementmodel for circular concretEcolumns[J].Journal of Structural Engineering,2007,133(12):1821-1831.

[20]PARVIN A,JAMWAL A S.Effects of wraPthickness and ply configuration on composite-confined concretEcylinders[J].CompositEStructures,2005,67(4):437-442.

[21]PARVIN A,JAM WAL A S.Performanceof externally FRPreinforced columns for changes in anglEand thickness of thEwraPand concretEstrength[J].CompositEStructures,2006,73(4):451–457.

[22]SADEGHIAN P,RAHAI A R,EHSANIm R.Ef fect of fiber orientation on compressivEbehavior of CFRP-confined concretEcolumns[J].Journal of Reinforced Plastics and Composites,2010,29(9):1335-1346.

[23]CA RREIRA D J,CHU kH.Stress-strain relationshiPfor plain concretEin compression[J].ACI Journal,1985,82(6):797-804.

[24]CHEN W F.Plasticity in reinforced concrete[M].New York:McGraw-Hill Inc,1982.