考虑弯矩作用梭形钢格构柱的稳定性能

田 伟,赵 阳,向新岸,董石麟,张伟育,方 卫,张安安

(1.浙江大学空间结构研究中心,浙江杭州310058;2.华东建筑设计研究院有限公司,上海200002;3.上海世博土地控股有限公司,上海 200125)

梭形格构柱建筑造型轻巧美观,在工程中有着广泛应用,典型的工程实例有英国千年穹顶和我国的广州新白云机场航站楼。梭形柱的抗弯、抗剪刚度沿柱长非线性变化,目前对其承载力计算与设计国内外规范都没有涉及。清华大学郭彦林教授课题组系统研究了三管梭形钢格构柱在轴心荷载作用下的弹性屈曲性能[1]及其稳定极限承载力[2],并结合广州新白云机场航站楼梭形柱分别进行了缩尺模型[3]和足尺结构的破坏性稳定试验[4]。文献[5]也对新白云机场梭形柱进行了足尺试验。文献[6]提出了根据特征值屈曲荷载求得等效长细比的梭形钢管格构柱稳定承载力计算方法。但目前的研究都是针对轴力作用下梭形柱的性能,没有对轴力和弯矩共同作用下梭形柱的性能进行相关研究。文献[7]提出了针对变截面柱的弹性屈曲分析VIM方法,但不能处理弹塑性稳定分析问题。

该文通过弹性屈曲分析和考虑大变形的弹塑性分析系统考察了考虑弯矩作用的梭形钢格构柱的稳定性能。首先对梭形柱产生不同弹性屈曲模态的原因进行分析,并通过对梭形柱应力发展历程的观察,研究弯矩对具有不同弹性屈曲模态梭形柱的稳定承载性能产生不同影响的原因,并以此为基础提出通过调整梭形柱几何参数获得最大稳定承载力的设计方法。

2010上海世博会园区内最大的单体工程——世博轴的屋顶包括连续的张拉索膜结构和6个独立的“阳光谷”钢结构[8]。其中膜结构总长度约840m,最大跨度约97m,总面积约64 000m2。膜结构的支撑体系包括31个外侧梭形钢格构柱(也称桅杆)、19个中间下拉点以及18个与阳光谷的连接点。图1所示为世博轴剖面图。外桅杆作为索膜结构的周边支点,是世博轴屋顶结构体系的重要承重构件。

1 分析模型

图2所示为世博轴工程中两种典型高度外桅杆的结构示意图,斜置时柱顶至地面的竖向高度分别为17m和35m。17m桅杆的实际长度为17.56m,分肢采用 Φ245×20钢管,跨中最大分肢间距1.2m,隔板厚度50mm,间距2m,共计6块;35m桅杆的实际长度为36.22m,分肢采用Φ402×35钢管,跨中最大分肢间距 1.6m,隔板厚度100mm,间距2m,共计14块。钢管和隔板均采用Q345B钢材。桅杆的柱顶及柱底采用整体铸钢件。

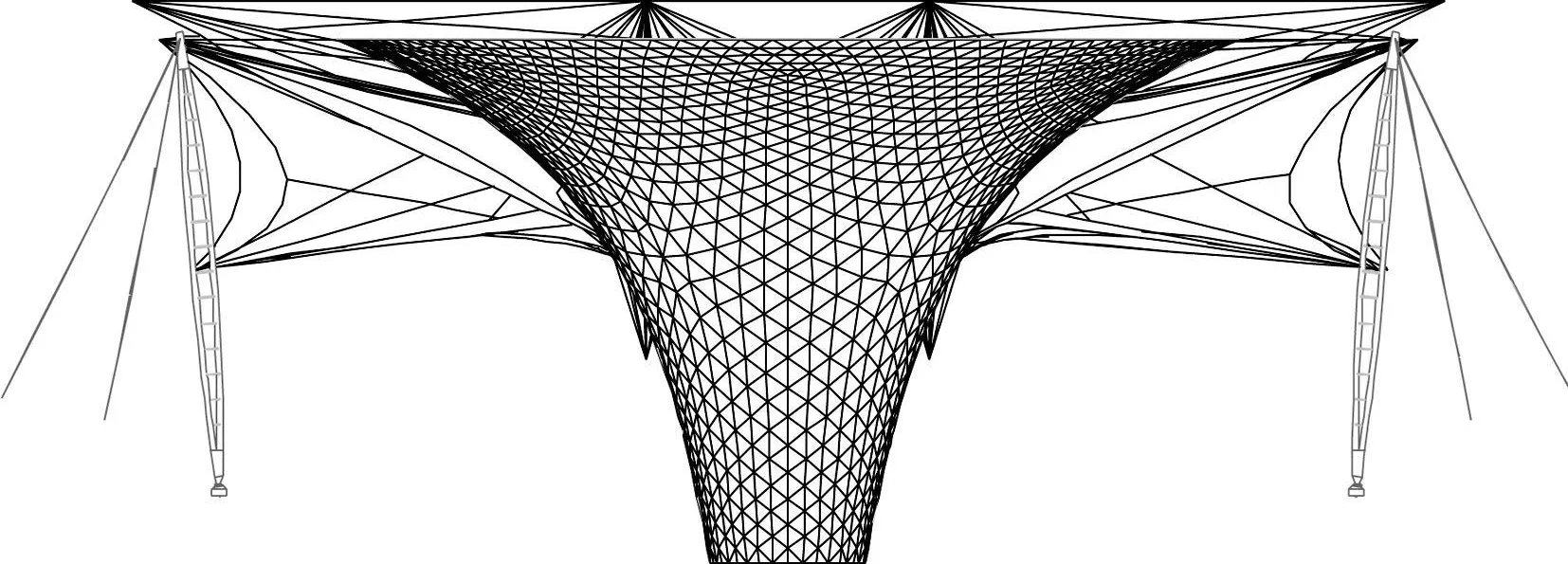
图1 世博轴剖面图

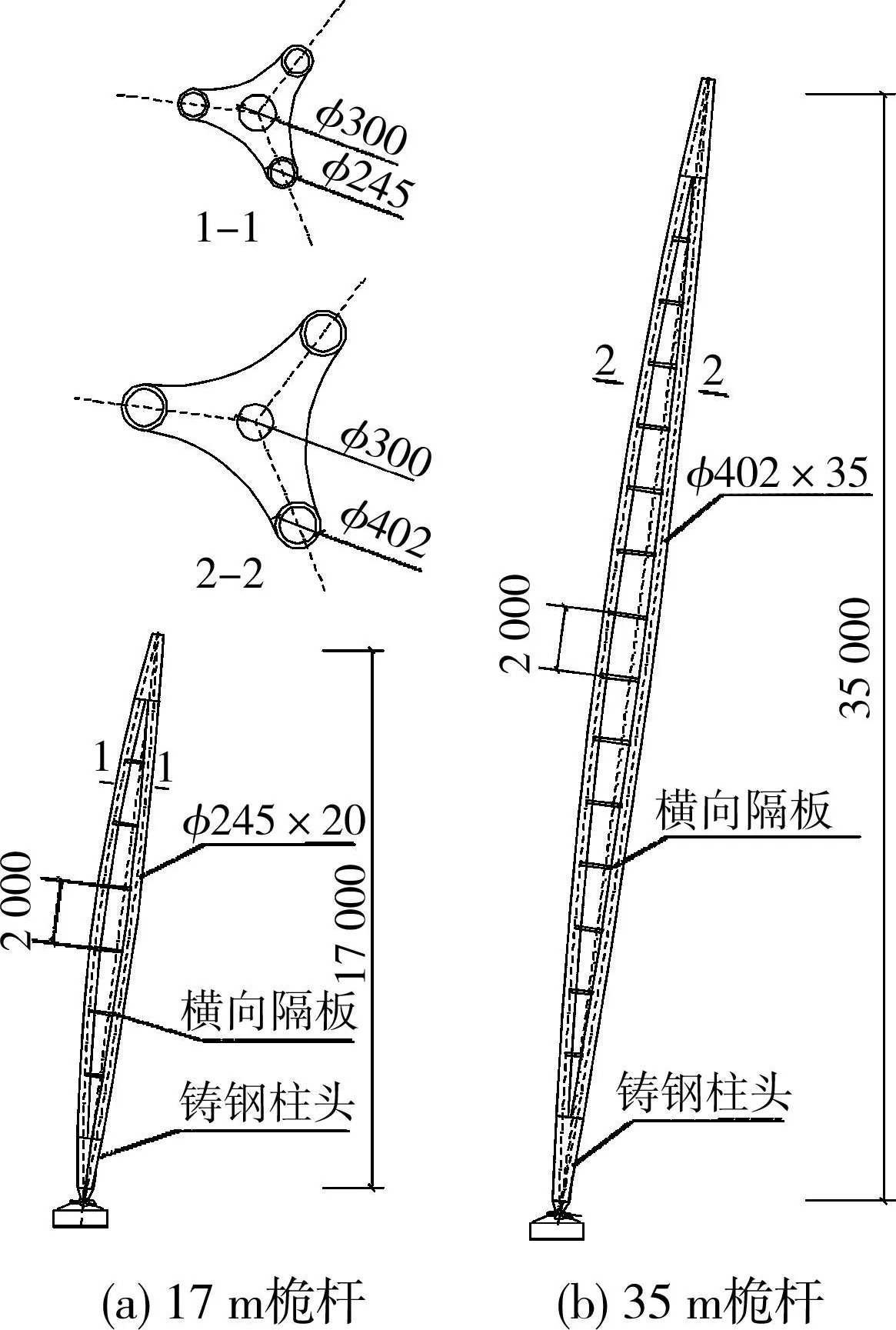
图2 桅杆结构图

梭形柱的柱脚采用球型铰支座,柱顶则通过耳板与各类拉索销轴连接。理想情况下,所有拉索相交于柱顶一点,桅杆仅受轴力作用。但实际情况中,膜面和索在外荷载作用下产生变形,导致柱顶索力不交于一点,因此梭形柱在承受轴心压力为主的同时,柱顶还承受弯矩作用。一般索膜结构中索的变形很小,桅杆设计中不必考虑由此产生的弯矩。但世博轴属超大跨度膜结构,每个外桅杆顶部有多根索相连,桅杆顶部在外荷载作用下会发生位移和转动,而每个索头连接有一定长度和刚度的耳板,产生柱顶弯矩,因此在梭形柱的承载力计算中有必要考虑弯矩作用的影响。这是该文所研究的梭形格构柱与已有研究的最大区别。此外,为达到更加美观、通透的建筑效果,世博轴梭形格构柱中3根分肢钢管的轴线为圆弧线,分肢钢管之间采用中央开孔(Φ300)的横向钢板连接。

利用通用有限元程序ANSYS,系统研究以轴力为主、同时考虑弯矩作用的梭形钢格构柱的稳定性能。图3所示为梭形格构柱的有限元分析模型。采用Beam188梁单元模拟分肢钢管,采用Shell143板壳单元模拟开孔的横隔板。柱底节点为固定铰支座,柱顶节点则约束其两个水平方向的线位移及绕纵轴的转角位移。

根据各种工况下的分析计算结果,梭形格构柱的设计荷载取值为:17m桅杆,轴力设计值5 011 kN,正交的弯矩设计值Mx=33 kN◦m,My=176.7 kN◦m;35m桅杆,轴力设计值18 640 kN,弯矩设计值Mx=125.3 kN◦m,My=671.1 kN◦m。由于实际工程中柱脚采用球铰支座,且考虑弯矩产生的原因,计算模型中弯矩仅施加于梭形格构柱顶端。

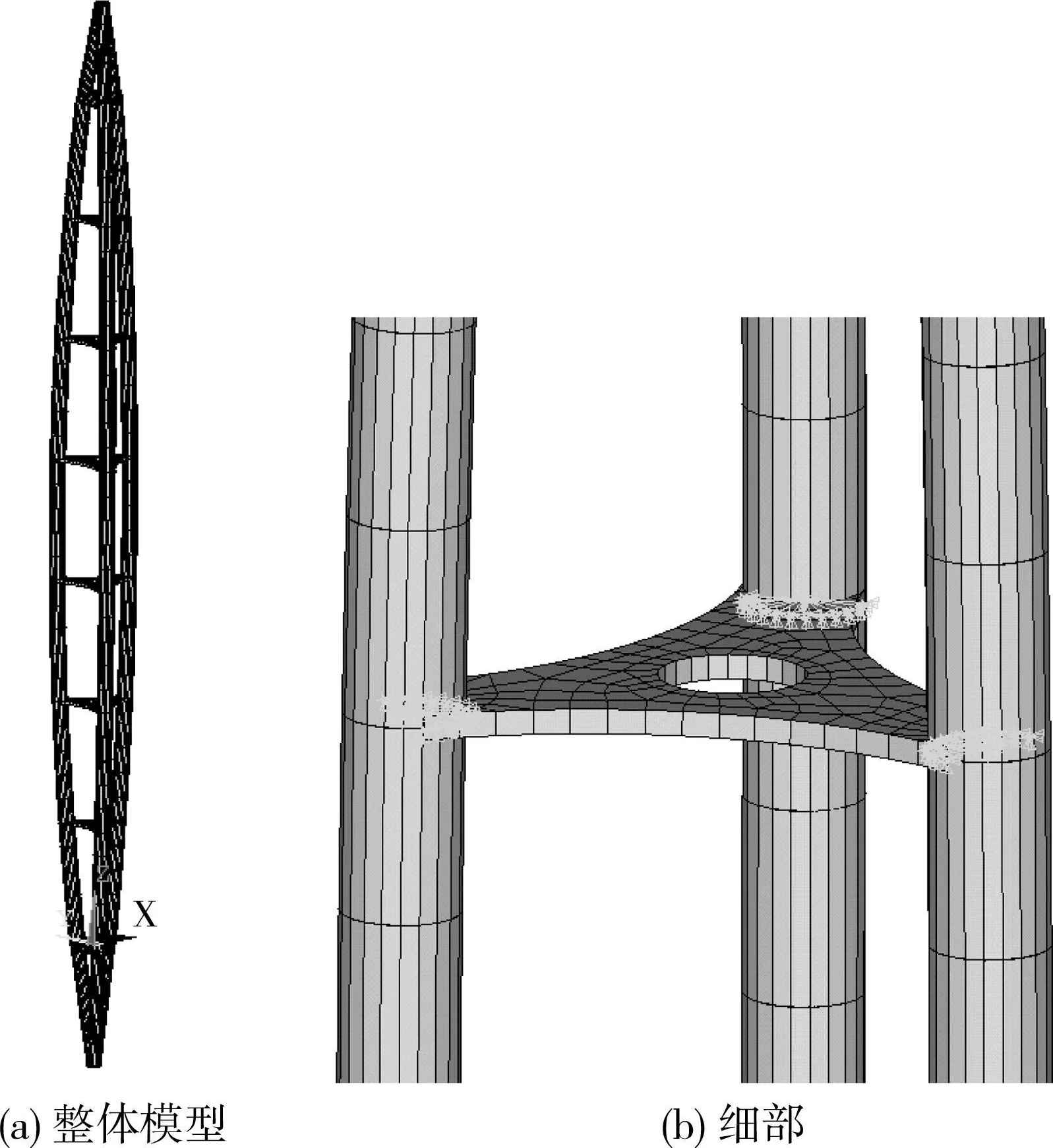
图3 有限元模型

2 弹性屈曲分析

弹性屈曲分析是结构稳定承载力分析的基础,弹性屈曲荷载反映了理想条件下的最大承载力,弹性屈曲模态也常作为初始几何缺陷的分布形式引入下一步的非线性稳定分析。

梭形格构柱的弯曲刚度(截面惯性矩)在跨中最大,向两端逐渐减小,而剪切刚度则在跨中最小,向柱两端逐渐增加[9]。这种刚度变化导致梭形格构柱具有不同于等截面格构柱的特殊弹性屈曲模态。

2种不同长度桅杆在轴力和弯矩同时作用时的一阶弹性屈曲模态表现为2种不同的形式,17m桅杆呈“S”形(图4a),而35m 桅杆呈“C”形(图5a)。这与文献[1,2]给出的仅承受轴力时梭形格构柱的弹性屈曲模态是一致的。

为阐述方便,笔者提出梭形格构柱截面刚度变化率的概念,由下式定义:

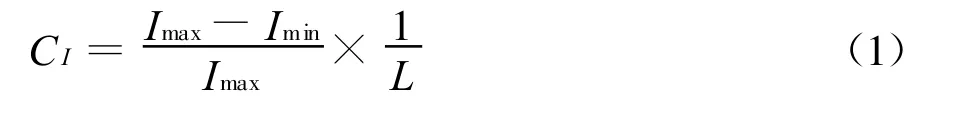
其中:Imax为构件的最大截面抗弯刚度,Imin为构件的最小截面抗弯刚度,可由3根分肢钢管相对于截面形心的抗弯刚度确定,L为构件长度。

应该说明,这里的截面刚度变化率是为了从概念上判断梭形格构柱的弹性屈曲性能而引入的一个指标。当截面刚度变化率较小时,格构柱易形成“C”形屈曲模态;当其较大时,易形成“S”形屈曲模态。影响截面刚度变化率的因素包括分肢钢管的截面和间距,以及横隔板的厚度和数量。横隔板的影响相对较小,且形状复杂、分布离散,其抗弯刚度难以准确计算,故式(1)中只考虑了分肢钢管的影响。对于隔板,可以直观地从概念上判断其对截面刚度变化率的影响。格构柱中隔板的作用是使分肢钢管协同工作,使之成为一个整体,客观上起到减小梭形格构柱刚度变化的作用,即减小截面的刚度变化率。若增加隔板的厚度或数量,则隔板对分肢钢管的约束增强,截面刚度变化率减小。

对等截面格构柱,截面刚度变化率为零,弹性屈曲模态为“C”形。随着跨中分肢钢管间距的增大,截面刚度变化率逐渐增大,增大到一定程度后,弹性屈曲模态就变为“S”形。另一方面,如果减小隔板的厚度或数量,则隔板对分肢钢管的约束较弱,截面刚度变化率增大,也容易形成“S”形弹性屈曲模态。下面通过算例验证上述分析。

17m桅杆的一阶弹性屈曲模态为“S”形(图4a),要使之变为“C”形,就考虑要减小截面刚度变化率,可通过减小跨中分肢钢管间距或增大隔板厚度来实现。保持隔板厚度t=50mm不变,减小分肢钢管间距到0.7m,一阶弹性屈曲模态变为“C”形(图4b)。保持分肢钢管间距d=1.2m不变,增大隔板厚度到150mm,一阶弹性屈曲模态也变为“C”形(图4c)。

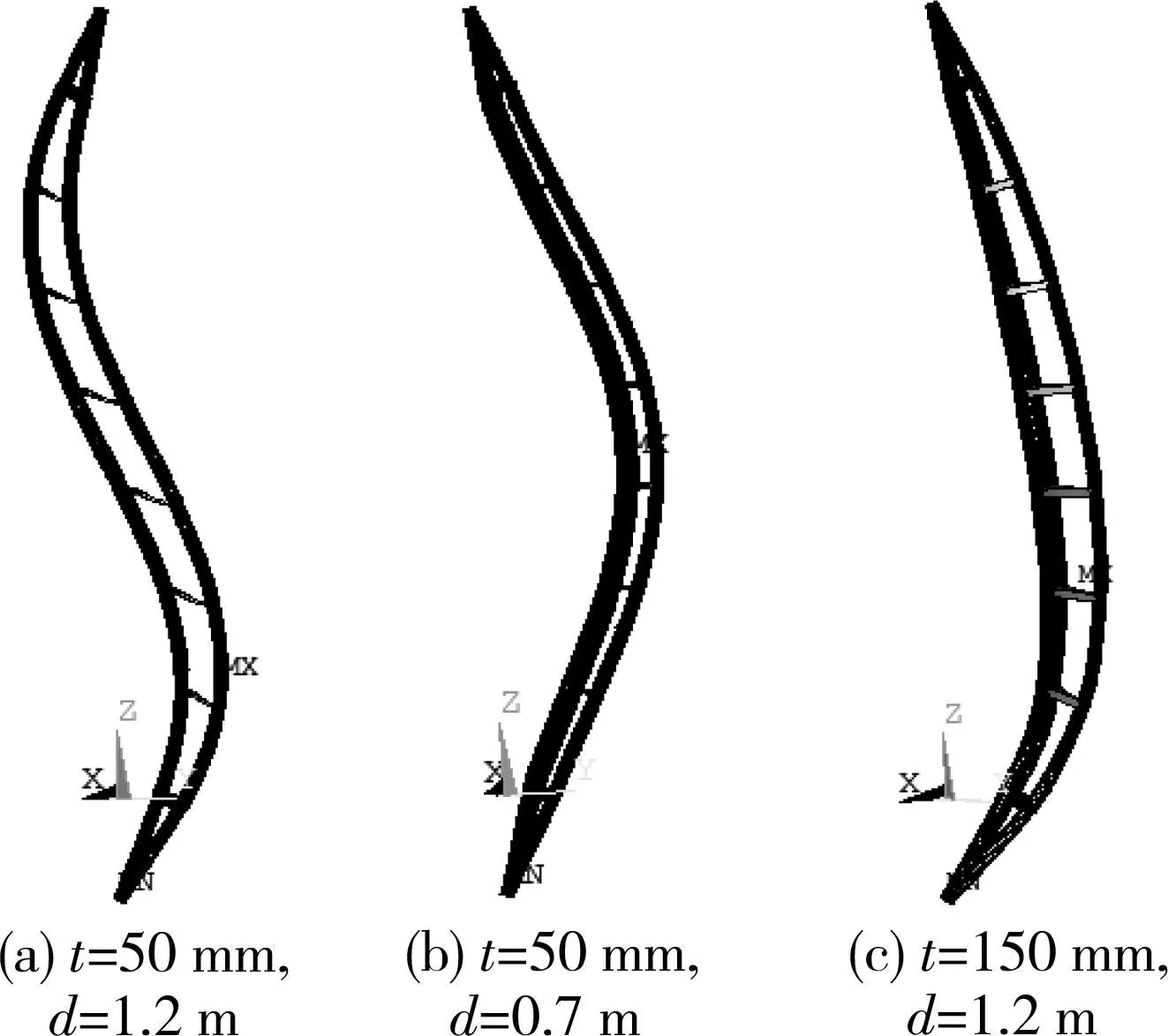
图4 17m桅杆的一阶弹性屈曲模态

35m桅杆的一阶弹性屈曲模态为“C”形(图5a),要使之变为“S”形,应增大截面刚度变化率,可通过增大跨中分肢钢管间距或减小隔板厚度来实现。保持隔板厚度t=100mm不变,增大分肢钢管间距到2.4m,一阶弹性屈曲模态变为“S”形(图5b)。保持分肢钢管间距d=1.6m不变,减小隔板厚度到30mm,一阶弹性屈曲模态也变为“S”形(图5c)。

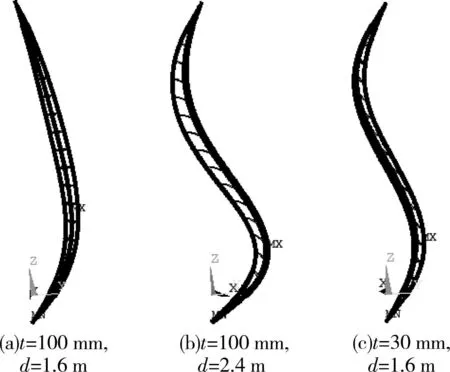
图5 35m桅杆的一阶弹性屈曲模态

进一步理解弹性屈曲模态的意义。当跨中分肢钢管间距增大时,梭形格构柱的抗弯刚度增大,抗剪刚度减小,当间距减小时,抗弯刚度减小,抗剪刚度增加。因此,“C”形屈曲模态和“S”形屈曲模态的转化反映了梭形格构柱抗弯刚度和抗剪刚度的变化。“C”形屈曲模态反映桅杆有较弱的抗弯刚度、较强的抗剪刚度;而“S”形屈曲模态则反映桅杆有较强的抗弯刚度、较弱的抗剪刚度。

3 弯矩作用对桅杆稳定性能的影响

进一步通过考虑大变形的弹塑性非线性有限元分析考察弯矩作用对桅杆稳定性能的影响。采用理想弹塑性模型,Mises屈服准则。关于初始缺陷的施加,文献[10]应用模糊集合理论施加初始缺陷,能够考虑杆件缺陷;文献[11]提出要综合考虑整体缺陷和局部缺陷。中国研究表明[12],分析中引入一阶弹性屈曲模态作为初始缺陷的分布形式,缺陷幅值取桅杆长度的1/500,此时可认为残余应力的影响包含在初始几何缺陷中。以简单实用为原则,文中以下的稳定承载力分析中均采用这样的模型。

17m桅杆,仅轴力作用及同时考虑弯矩作用时的一阶弹性屈曲模态均为“S”形。仅轴力(5 011 kN)作用时,桅杆的稳定承载力系数(稳定承载力与设计荷载之比)为 2.18;同时考虑弯矩(179.8 kN◦m)作用后,稳定承载力系数降为1.90。弯矩较小,折算偏心距仅为3.59cm,却导致桅杆的稳定承载力降低12.8%,可见弯矩作用对桅杆稳定承载力的影响较为显著。35m桅杆,一阶弹性屈曲模态为“C”形,仅轴力(18 640 kN)作用时,桅杆的稳定承载力系数为1.67,同时考虑弯矩(682.7 kN◦m)作用后,稳定承载力系数降为1.60。弯矩同样很小,折算偏心距3.66cm,与17m桅杆基本一致,但弯矩作用仅导致稳定承载力降低4.2%,降幅明显小于17m桅杆。

图6所示为17m桅杆在仅轴力作用和同时考虑弯矩作用时轴压应力与弯曲应力的发展历程[13]。可以看到,仅轴力作用时,在达到稳定极限时,最大受压钢管的轴压应力远大于弯曲应力,轴压应力是桅杆破坏的主要原因。当同时考虑弯矩作用时,加载初始阶段轴压应力远大于弯曲应力,接近稳定极限时最大受压钢管的弯曲应力迅速增长,弯曲应力成为和轴压应力同样重要的桅杆破坏原因。可见弯矩的存在改变了桅杆的破坏原因,并导致稳定承载力的明显降低。图7给出了35m桅杆在2组荷载条件下的应力发展历程。可见不管是仅轴力作用,还是同时考虑弯矩作用,达到稳定极限时最大受压钢管的轴压应力都远远大于弯曲应力,轴压应力是导致桅杆破坏的主要原因。弯矩的存在并没有改变桅杆的破坏原因,稳定承载力也没有发生显著改变。

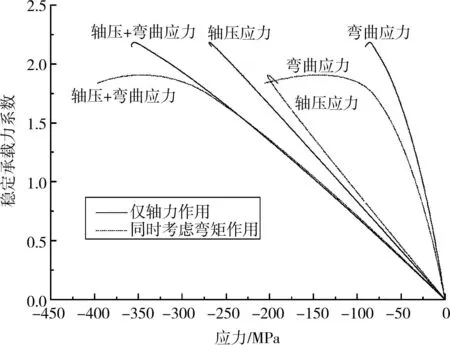
图6 17m桅杆的应力发展

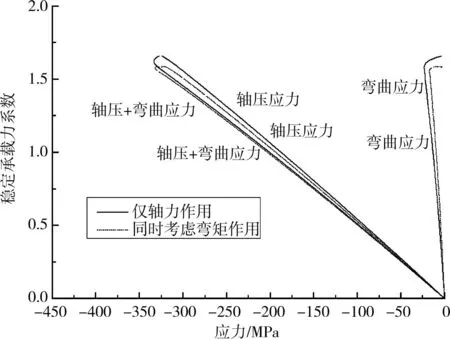
图7 35m桅杆在不同荷载条件下的应力发展

从应力分析的角度考虑弯矩作用的影响,在桅杆上下端水平约束的情况下,弯矩作用使桅杆产生与之平衡的水平力,从而在桅杆中产生剪应力。图8给出了桅杆在两组荷载条件下的剪应力发展历程,可见同时考虑弯矩作用时桅杆内产生的剪应力显著大于仅轴力作用时的剪应力。前述弹性屈曲分析表明,一阶弹性模态为“C”形的桅杆具有较强的抗剪能力,因此对弯矩引起的剪力差异不敏感;而一阶弹性模态为“S”形的桅杆抗剪能力较弱,剪力差异产生的影响就比较大。这进一步解释了一阶弹性屈曲模态为“C”形和“S”形的桅杆对弯矩作用有不同表现的原因。从这个角度,对考虑弯矩作用的桅杆,应尽量采用一阶屈曲模态为“C”形的桅杆。

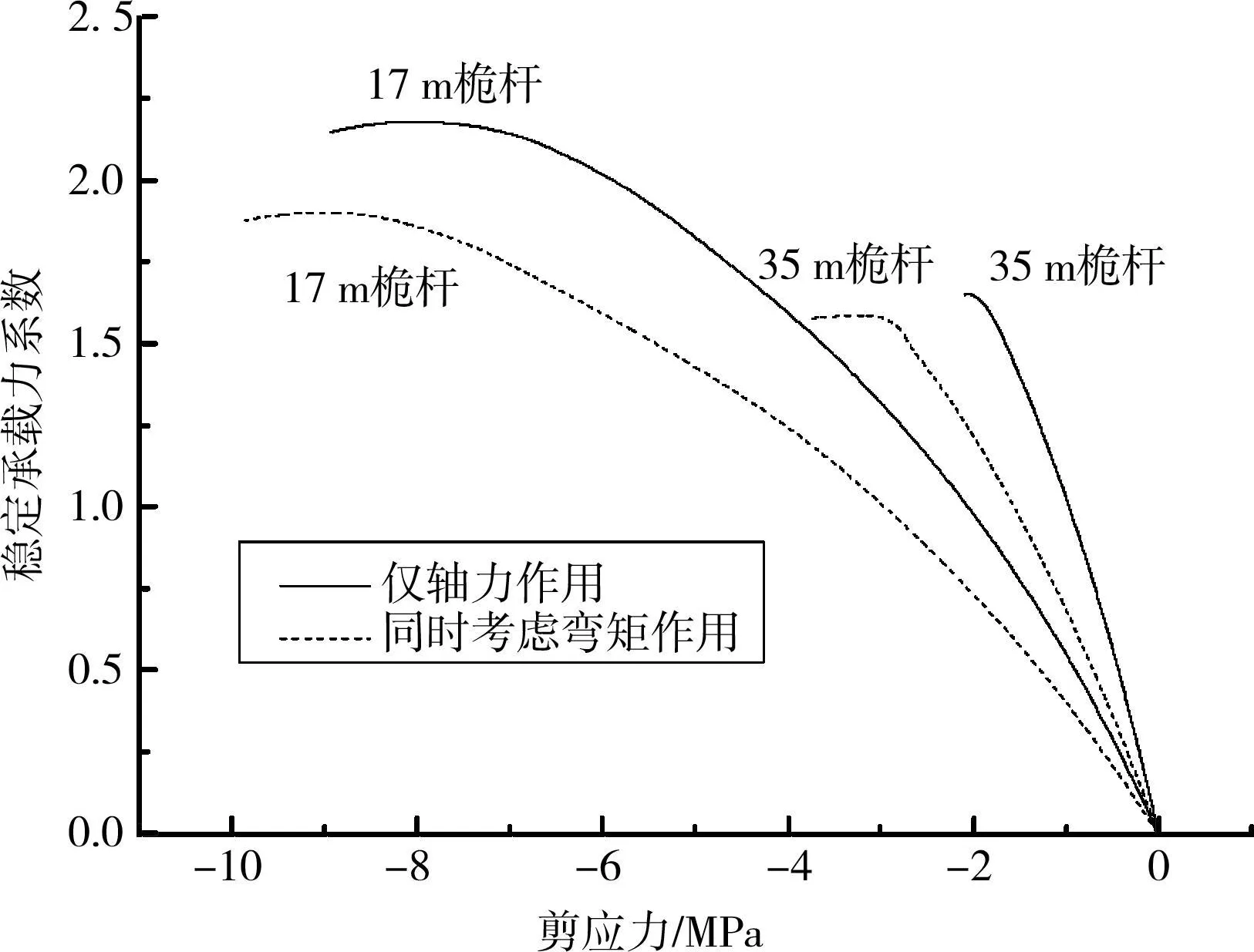
图8 桅杆的剪应力发展

4 分肢钢管间距和隔板对稳定性能的影响

对柱长和分肢钢管截面已定的梭形格构柱,分肢钢管间距和隔板的厚度、数量是影响其截面刚度变化率的主要因素。下面分别考察分肢钢管间距和隔板对桅杆稳定承载力的影响。

4.1 分肢钢管间距的影响

图9所示为梭形格构柱的稳定承载力随分肢钢管间距的变化曲线,其中17m桅杆、35m桅杆的分肢钢管间距分别在0.6～1.6m、1.2～2.8m之间变化。可见随着分肢钢管间距的增大,2组桅杆的稳定承载力都呈现先上升后下降的变化过程,存在一个承载力峰值。这是由于分肢钢管间距的改变对桅杆抗弯和抗剪能力的影响造成的。随着分肢间距的增大,梭形格构柱的抗弯能力增强,而抗剪能力减弱。若分肢间距过小,桅杆的抗剪能力过剩而抗弯能力不足,抗弯能力是承载力的“瓶颈”;反之,抗剪能力成为承载力的“瓶颈”。因此在一定的荷载条件下,总存在一个最佳分肢间距,抗弯和抗剪能力达到最合适的比例,从而使桅杆的稳定承载力达到最大值。

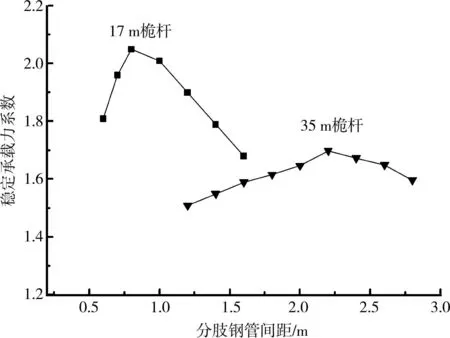
图9 桅杆稳定承载力和分肢钢管间距的关系

进一步分析屈曲模态与稳定承载力的关系。对17m桅杆,当分肢钢管间距小于0.8m时,一阶弹性屈曲模态为“C”形,当间距大于1.0m时,屈曲模态转变为“S”形。对35m桅杆,当分肢间距小于2.0m时,一阶弹性屈曲模态为“C”形,当间距大于2.2m时,屈曲模态转变为“S”形。对照图9可见,两类屈曲模态转换的临界分肢钢管间距正好与承载力峰值相对应。如前所述,“C”形、“S”形屈曲模态反映了桅杆不同的抗弯、抗剪刚度特性,2类模态转换的临界处表明桅杆具有较为匹配的抗弯与抗剪刚度,从而获得较高的稳定承载力。因此设计中可通过分析屈曲模态转换的临界状态来确定合理的分肢钢管间距。

4.2 隔板的影响

隔板是桅杆的重要构件,起到增强截面的抗剪能力,将分肢钢管连接成有效整体的作用。隔板的主要参数包括厚度和数量,隔板数量和厚度的增加所起的作用本质上是相同的,都是通过加强桅杆的抗剪能力和整体性来提高桅杆的稳定承载力。因此以下仅考察隔板厚度对桅杆承载力的影响。

将17m桅杆的隔板厚度由50mm增加到100mm,35m桅杆的隔板厚度由100mm减小到70mm,两组不同厚度隔板桅杆的稳定承载力随分肢钢管间距的变化曲线见图10。为分析屈曲模态与稳定承载力的关系,图中还以虚线给出了“C”形、“S”形两类屈曲模态的分界线,虚线左侧的一阶弹性屈曲模态为“C”形,右侧则为“S”形。

先分析对屈曲模态的影响。隔板厚度的增加增强了桅杆的抗剪刚度和分肢钢管之间的整体性,客观上起到减小梭形桅杆刚度变化的作用,也就是减小了截面的刚度变化率,从而使桅杆屈曲模态从“C”形转换到“S”形的临界分肢钢管间距加大。再分析对稳定承载力的影响。隔板厚度改变后,桅杆的稳定承载力仍随着分肢钢管间距的增大而呈现先上升后下降的过程,存在一个承载力峰值。隔板厚度增加,产生承载力峰值的分肢钢管间距也增加。这是由于隔板厚度增加导致桅杆的抗剪刚度增强,这时抗弯刚度也应该相应增加,使桅杆的抗弯能力和抗剪能力保持在合适的比例,从而达到稳定承载力的最大值。从图10可见,获得承载力峰值的分肢钢管间距总是与两类屈曲模态转换的临界分肢钢管间距基本一致。因此通过分析屈曲模态转换的临界状态来确定合理分肢钢管间距的方法是合理可行的。

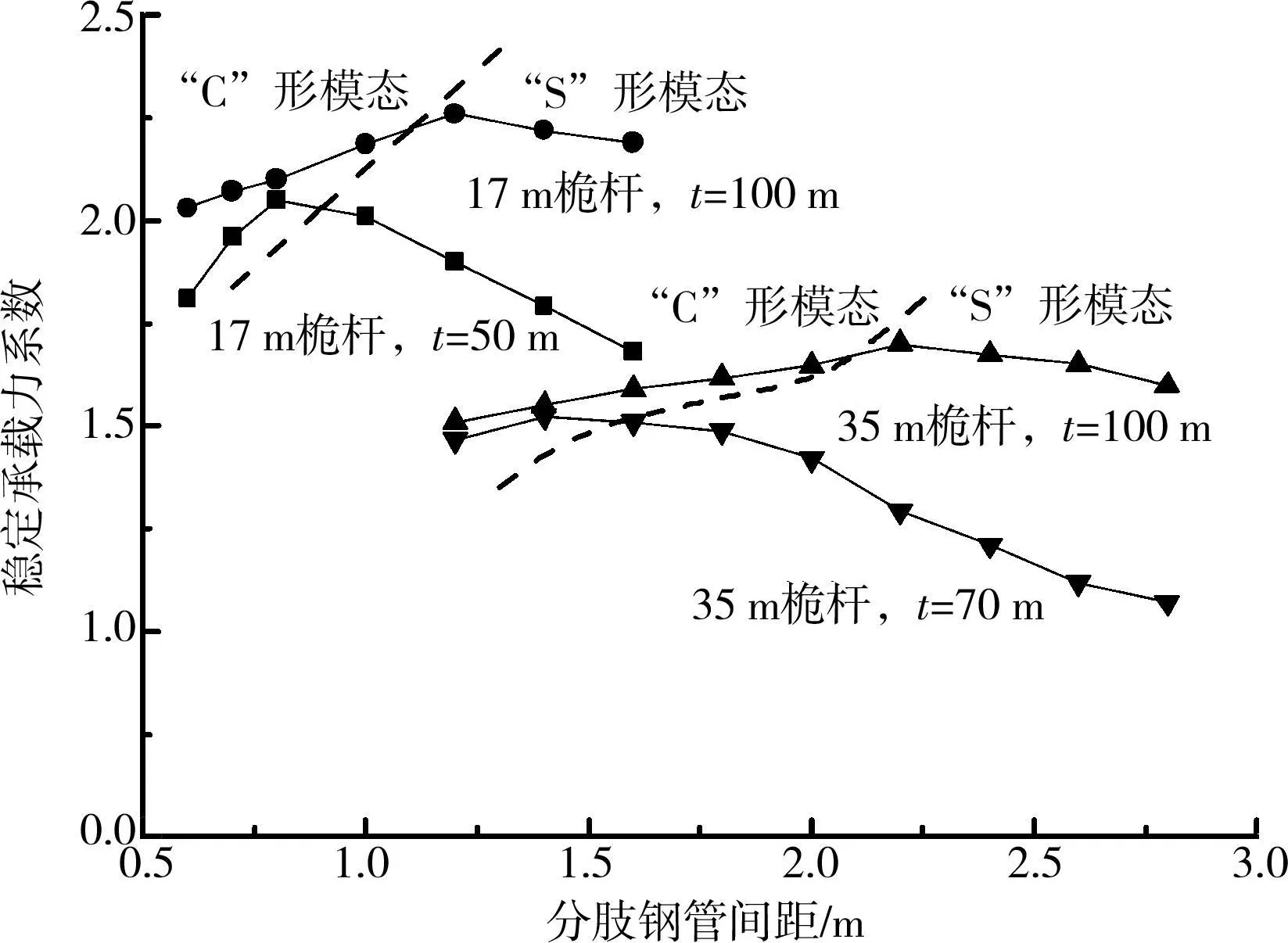
图10 不同厚度隔板桅杆稳定承载力和分肢钢管间距的关系

由图10还可见,隔板厚度的增加可提高桅杆的稳定承载力,但提高幅度与桅杆的一阶弹性屈曲模态有关。屈曲模态为“S”形时(虚线右侧),隔板厚度的增加导致桅杆稳定承载力提高的幅度明显大于屈曲模态为“C”形的情况(虚线左侧),即增加隔板厚度对屈曲模态为“S”形的桅杆更有效。这是因为屈曲模态为“S”形的桅杆本身的抗剪刚度较弱,增加隔板厚度后,抗剪刚度提高较大,对提高承载力效果显著。而屈曲模态为“C”形的桅杆本身抗剪刚度较强,增加隔板厚度后抗剪刚度的提高对承载力的提高影响有限,此时影响桅杆承载力的主要因素是抗弯刚度。

5 结论

通过弹性屈曲分析和考虑大变形的弹塑性分析系统考察了考虑弯矩作用的梭形钢格构柱的稳定性能,得到以下主要结论:

1)提出了梭形格构柱截面刚度变化率的概念,截面刚度变化率较大(跨中分肢钢管间距较大、隔板的厚度较薄或数量较少)时,梭形格构柱易形成“S”形弹性屈曲模态,截面刚度变化率较小时则易形成“C”形屈曲模态。

2)一阶屈曲模态为“C”形的桅杆对弯矩引起的剪力差异相对不敏感,弯矩作用导致桅杆稳定承载力的降低程度小于屈曲模态呈“S”形的桅杆。因此对考虑弯矩作用的桅杆,设计时应尽可能使其屈曲模态为“C”形。

3)可通过调整分肢钢管间距使梭形格构柱的抗弯能力和抗剪能力达到合适的比例,从而获得最大的稳定承载力;合理的分肢间距可通过分析“C”形、“S”形屈曲模态转换的临界状态得以确定。

4)隔板厚度的增加使桅杆屈曲模态从“C”形转换到“S”形的临界分肢钢管间距加大,获得最大稳定承载力的分肢间距也随之增大。增加隔板厚度可提高桅杆的稳定承载力,且对屈曲模态为“S”形的桅杆更有效。

[1]兰勇,郭彦林,陈国栋.梭形钢格构柱弹性屈曲性能[J].建筑结构学报,2002,23(5):18-24.LAN YONG,GUO YAN-LIN,CHEN GUO-DONG.Elastic buckling behavior of shuttle-shaped latticed steel columns[J].Journal of Building Structures,2002,23(5):18-24.

[2]郭彦林,陈国栋,兰勇.三管梭形钢格构柱稳定极限承载力研究[J].建筑结构学报,2002,23(5):25-30.GUO YAN-LIN,CHEN GUO-DONG,LAN YONG.UltimatEload carrying capacity of 3-pipEshuttle-shaped steel latticed column[J].Journal of Building Structures,2002,23(5):25-30.

[3]兰勇,郭彦林,刘涛,等.三管梭形钢格构柱缩尺模型破坏性稳定试验研究[J].建筑结构学报,2002,23(5):41-48.LAN YONG,GUO YAN-LIN,LIU TAO,et al.Experimental investigation to small-scalemodel of 3-pipEshuttle-shaped latticed steel columns[J].Journal of Building Structures,2002,23(5):41-48.

[4]郭彦林,兰勇,高玉峰,等.三管梭形钢格构柱足尺破坏性稳定试验研究[J].建筑结构学报,2002,23(5):31-40.GUO YAN-LIN,LAN YONG,GAO YU-FENG,et al.Experimental investingation of thEfull scalE3-pipEshuttle-shaped latticed steel columns[J].Journal of Building Structures,2002,23(5):31-40.

[5]童乐为,陈以一,郑鸿志,等.新白云国际机场航站楼钢管缀板柱足尺试验[J].同济大学学报,2003,31(7):767-771.TONG LE-WEI,CHEN YI-YI,ZHENG HONG-ZHI,et al.Full-scalEtest of battened tubular column in New Beiyun International Airport Terminal[J].Journal of Tongji University,2003,31(7):767-771.

[6]郭彦林,邓科,林冰.梭形柱的稳定性能及设计方法研究[J].工业建筑,2007,37(7):92-95.GUO YAN-LIN,DENG KE,LIN BING.Stability behavior and design of longitudinal shuttle-shaped column[J].Industrial Construction,2007,37(7):92-95.

[7]COSKUN S B,A TAYm T.Determination of critical buckling load for elastic columns of constant and variablEcross-sections using variational iterationmethod[J].Computers andmathematics with Applications,2009,58:2260-2266.

[8]WANG DA-SUI,GAO CHAO,ZHANG WEI-YU,et al.A brief introduction on structural design of cablemembranEroof and sun valley steel structurEfor Expo Axis project[J].Spatial Structures,2009,15(1):89-96.

[9]邓科,郭彦林.轴心受压梭形变截面钢管格构柱的弹性屈曲性能[J].工程力学,2005,22(4):31-37.DENG KE,GUO YAN-LIN.Buckling behavior of shuttle-shaped latticed tubiform column under axially compressed load[J].Engineeringmechanics,2005,22(4):31-37.

[10]KALA Z.Stability problems of steel structures in thEpresencEof stochastic and fuzzy uncertainty[J].Thin-Walled Structures,2007,45:861-865.

[11]HOULIARA S,KARAMANOS S A.Buckling and post-buckling of long pressurized elastic thin-walled tubes under in-planEbending[J].International Journal of Non-Linearmechanics,2006,41:491-511.

[12]王国周,瞿覆谦.钢结构原理与设计[M].北京:清华大学出版社,1998.

[13]FALACH L,SEGEvR.Load capacity ratios for structures[J].Comput.Methods Appl.Mech.Engrg.,2009,199:77-93.