桥墩及桩基形式对墩底平转施工转盘设计的影响
2020-03-30秦寰宇
秦寰宇
(中铁第四勘察设计院集团有限公司,武汉 430063)
为减小新建铁路施工对既有线运营的影响,常采用平转转体方法施工跨越既有线的桥梁[1]。平转转体分为墩顶转体[2]和墩底转体2 种方式,且普遍采用墩底转体方式[3-4]。墩底平转转体桥梁转盘设计主要包括上转盘设计和下转盘(即转体桥梁的承台)设计。上下转盘的受力与桥墩类型和桩基布置密切相关,如果选择的墩型或桩基布置不合适,将导致上下转盘的受力状态较差,造成上下转盘的尺寸、配筋或配索增加,从而增加建造成本。为解决上述问题,本文以新建福厦高速铁路西溪特大桥(94+168+94)m 平转转体刚构为背景,分析不同墩型对上转盘受力的影响以及不同桩基布置对下转盘受力的影响,并对桥墩及桩基进行优化,为转体设计中桥墩及桩基的选型和优化提供参考。
1 工程概况
新建福厦高速铁路西溪特大桥(94+168+94)m 刚构,上跨既有铁路,梁部采用预应力混凝土箱梁,梁宽12.6 m,边支点梁高4.5 m,中支点梁高10.5 m,平行于既有铁路悬灌施工,悬灌至最大悬臂长度83 m 后进行转体、封铰,最后合龙[5]。该桥采用平转转体施工方法进行施工,上、下转盘的尺寸分别为15 m(长)×15 m(宽)×3.5 m(高),16.8 m(长)×22.8 m(宽)×5.6 m(高);转体吨位为17 500 t,球铰无偏心。转体施工半立面见图1。
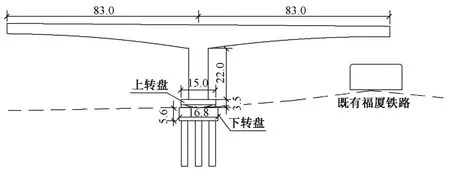
图1 转体施工半立面(单位:m)
2 桥墩对上转盘设计影响
铁路桥梁中,常采用的墩型包括实体墩、空心墩及双薄壁墩。本文分别采用这3种墩型对转体刚构上转盘进行实体有限元分析,探究不同墩型对上转盘受力的影响规律,从而确定最终方案并对其优化。
2.1 有限元分析
大桥墩高22 m,顺桥向厚7 m,横桥向宽9 m,采用MIDAS FEA对上转盘及桥墩底部8 m高度范围建立实体有限元模型[6],并对转体工况进行分析。根据圣维南原理,在墩底以上8 m 高度处可认为压力已经均匀分布,因此将墩底8 m 以上部分的重力按均布荷载施加在模型的顶部,并对上转盘球铰底部的接触面进行约束。经计算,转体工况下3 种桥墩主拉应力云图见图2。
由图2 可知:实体墩最大主拉应力为0.52 MPa,位于上转盘以上1 m 高度处;空心墩、双薄壁墩最大主拉应力分别为4.29,9.09 MPa,均位于上转盘顶部。
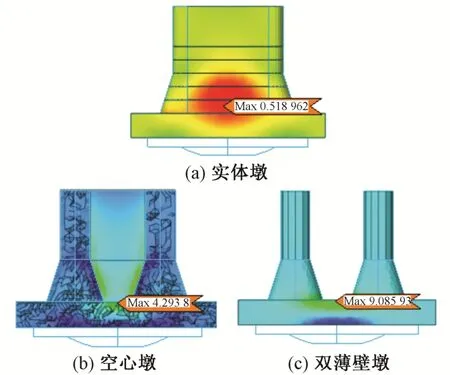
图2 桥墩主拉应力云图(单位:MPa)
转体工况下,由于球铰支承上转盘造成上转盘顶部中心产生较大的主拉应力,而墩身混凝土对上转盘起到一定的约束作用,即实体墩>空心墩>双薄壁墩。约束越强,所受主拉应力越小。因此产生的主拉应力大小为实体墩<空心墩<双薄壁墩。据此推断,增加墩底实体段可加强墩底混凝土对上转盘的约束作用,减小转体工况下产生的主拉应力。
对空心墩及双薄壁墩增加1~5 m 墩底实体段,以米为单位进行有限元计算,分析墩底实体段高度对转体主拉应力的影响。计算结果表明,最大主拉应力均出现在墩底实体段顶部,将墩底实体段高度及最大主拉应力的关系绘成曲线,见图3。
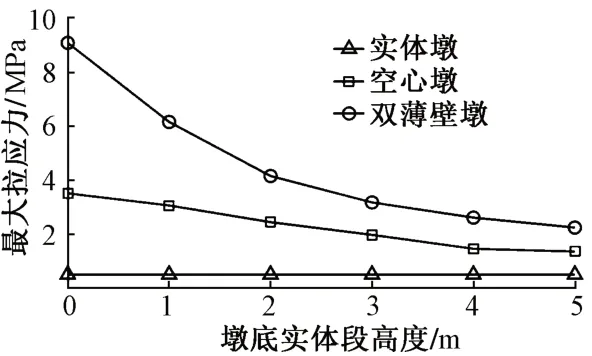
图3 墩底最大主拉应力曲线
由图3可知:①实体墩对上转盘受力最有利,其次是空心墩,最不利的是双薄壁墩;②通过增加墩底实体段,能够有效降低空心墩、双薄壁墩上转盘的主拉应力;③随着墩底实体段高度的增加,主拉应力降低的幅度逐渐变小。
2.2 桥墩方案选型及优化
在墩高较矮时采用实体墩,既能有效减小转体工况下的墩底主拉应力,又不会过多增加自重;在墩高较高时,为减轻桥墩重量、减小转体吨位,可采用空心墩或双薄壁墩,并在墩底增加一定厚度的实体段,以减小转体工况主拉应力。
本桥桥墩尺寸为22 m(高)×9 m(宽)×7 m(厚),尺寸较大。结合墩梁固结处受力[7]、球铰吨位、美观等方面综合考虑,拟采用双薄壁墩。为减小上转盘主拉应力,在墩底增加2.0 m 高实体段对其进行优化。纵桥向距实体段顶面 0.3 m 高度处布置 17 根 12-φ15.2 的钢索;横桥向距实体段顶面0.5 m 高度处布置9 根12-φ15.2 的钢索。钢索平面间距均为0.5 m,并沿墩中心向两侧布置,见图4。
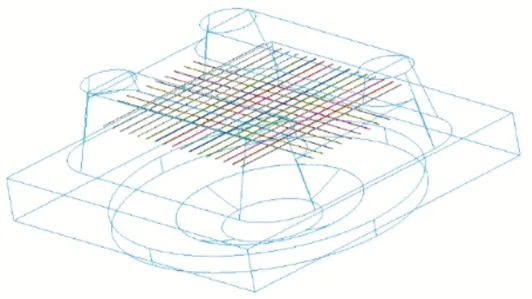
图4 墩底实体段钢索布置
经计算,实体段顶面最大主拉应力为2.4 MPa(图5)。因此,墩底实体部分可以采用C50 混凝土,保证施工过程中混凝土不开裂。

图5 墩底应力云图(单位:MPa)
3 桩基对下转盘设计的影响
铁路桥梁中常采用的桩基布置形式为梅花式和行列式。本文采用这2种布桩形式对转体刚构下转盘进行实体有限元分析,探究不同桩基布置对下转盘受力的影响规律,从而确定最终方案并对其优化。
3.1 有限元分析
大桥基岩距地面线31 m,桩基础采用柱桩。采用MIDAS FEA 对下转盘及桩基础建立实体有限元模型,对转体工况进行分析。将球铰以上部分的结构重力施加在下转盘球铰接触面上。由于转体过程中悬臂平衡,主要受力为竖向力,且桩基础为柱桩,因此不考虑土层的侧向约束,仅对桩底进行约束。
选取梅花式及行列式2 种方案,桩径均为2.8 m,下转盘厚度采用2倍桩径[8-9]。桩基平面布置见图6。
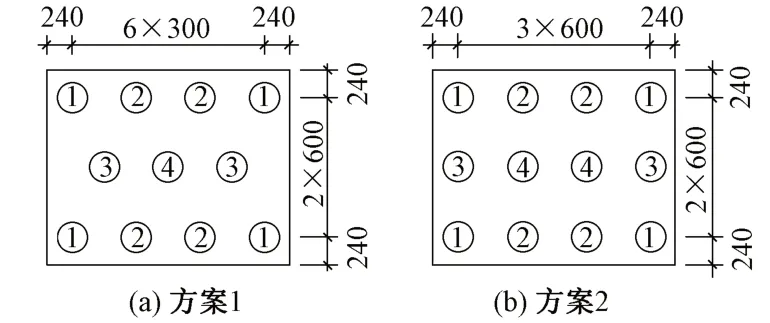
图6 桩基平面布置(单位:cm)
由于球铰与下转盘接触面较小,造成下转盘底部中心产生较大主拉应力。利用有限元建模分析,2 种布桩形式下转盘底部主拉应力云图见图7。可知,方案1 和方案2 下转盘底部最大主拉应力分别为4.44,5.61 MPa。
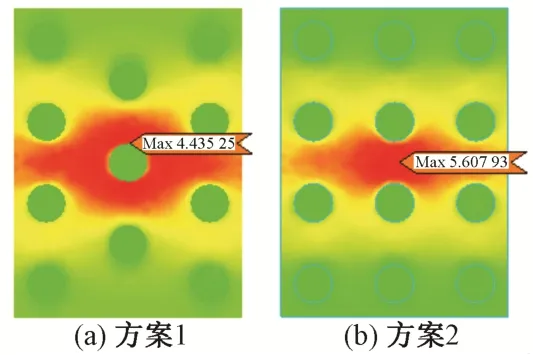
图7 下转盘底主拉应力云图(单位:MPa)
1—4号桩的最大轴力见表1。

表1 桩基最大轴力 kN
由图7 和表1 可知:①球铰正下方布置桩基时,对下转盘底部受力更加有利;②距离球铰中心越远,桩基所受到的力越小,中桩受力明显大于角桩。
3.2 桩基方案选型及优化
桩基布置时应尽量选择在球铰下方设置桩基的布置形式,以减小下转盘底部主拉应力。在转体工况下,中桩受力明显大于边桩,可适当增加中桩桩径,使各桩基应力状态更加均衡。对于方案1和方案2,中桩及角桩最大轴力相差不到10%,但方案1 能有效减小下转盘底部主拉应力。因此,拟采用方案1 的桩基布置形式。由于桩基对下转盘的支承不是绝对刚性的,各桩基转体状态下承受的荷载在成桥后会重分配。因此,桩基计算时对封铰前的荷载进行重分配以及不进行重分配2种工况进行包络计算。
本文采用自主开发的“预应力混凝土双柱门式墩结构分析软件”中桩基计算模块[10]对桩基进行包络计算。为使各桩基应力状态更加均衡,且满足最小桩间距的要求,拟优化中桩桩径至3.0 m,其他桩基尺寸及布置均不变。根据优化后的桩基布置重新进行建模设计。纵桥向距下转盘底面0.3 m 高度处布置21 根15-φ15.2的钢索;横桥向距下转盘底面0.55 m高度处布置21 根25-φ15.2 的钢索。钢索平面间距均为0.5 m,并沿下转盘中心向两侧布置,见图8。
经计算,转体工况下转盘底的主拉应力为1.3 MPa(图9),下转盘混凝土可采用C30。
图8 下转盘钢索布置
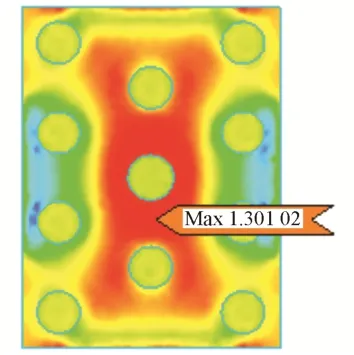
图9 转体工况下转盘底主拉应力云图(单位:MPa)
4 结论
1)实体墩对上转盘受力最有利,其次是空心墩,最不利的是双薄壁墩。
2)增加墩底实体段,能够有效降低空心墩、双薄壁墩上转盘的主拉应力。随着墩底实体段高度的增加,主拉应力降低的幅度逐渐变小。
3)球铰正下方有桩基时,对下转盘受力更加有利。距离球铰中心越远,桩基所受到的力越小,适当增加中桩桩径,可使各桩基应力状态更加均衡。
