带预应力约束拉杆R-CFT短柱轴压性能试验研究

李俊华,王建民,李玉顺

(宁波大学建筑工程与环境学院,浙江宁波315211)

在多、高层建筑中采用矩形、异形钢管混凝土柱能较好地满足建筑平面布置要求,有效避免柱角外露,增加房屋使用净空,因此在我国许多工程中得到了应用。然而矩形、异形钢管混凝土柱中,钢管壁对核心混凝土所能提供的约束作用不如圆形钢管混凝土柱,荷载作用下矩形、异形钢管长边由于宽厚比相对较大,更容易发生局部屈曲,因此矩形、异形钢管混凝土柱的承载力和延性都不如圆形钢管混凝土柱[1-7]。为了改善矩形、异形钢管混凝土柱的力学性能,有学者提出在构件长边方向每隔一定间距布置约束拉杆,形成带约束拉杆钢管混凝土柱。已有研究表明,这种约束拉杆的布置,能够有效延缓钢管壁的局部屈曲,改善钢管壁对混凝土的约束效应,提高构件的承载力与延性,是进一步完善矩形、异形钢管混凝土柱受力性能的有效途径[8-16]。

带普通约束拉杆钢管混凝土柱中,约束拉杆对构件力学性能的影响主要在于2个方面,首先约束拉杆能对钢管壁提供侧向支撑,防止钢管壁过早发生局部屈曲;其次约束拉杆起类似于箍筋作用,对核心混凝土提供附加约束,提高混凝土的强度和极限变形能力。普通约束拉杆对钢管壁以及核心混凝土的这种约束作用是一种被动约束,只有当构件产生一定膨胀和横向变形以后才能发挥效应。论文提出采用预应力约束拉杆,即在构件受荷前,对约束拉杆进行预拉从而在钢管壁和核心混凝土中产生横向预压力,以期进一步改善钢管混凝土柱的力学性能。为探索这种新型约束拉杆的有效性,设计了3个带预应力约束拉杆的矩形钢管混凝土短柱试件和另外2个对比试件,并对其进行了轴向荷载下的试验研究。

1 试验概况

1.1 试件设计与制作

试验设计了3个带预应力约束拉杆矩形钢管混凝土短柱试件,试验参数为约束拉杆间距和截面长宽比;为了考察预应力约束拉杆、普通约束拉杆以及无约束拉杆时构件受力性能的差异,还特设计了1个带普通约束拉杆和1个不带约束拉杆的对比试件。预应力约束拉杆和普通约束拉杆均由公称长度为160mm的10.9级M20高强度螺栓组成,作为普通约束拉杆的高强度螺栓,在构件受轴向压力前,通过螺栓垫板与钢管壁围焊连成一整体,构件受荷前拉杆不受力;作为预拉力约束拉杆的高强度螺栓,在构件受轴向压力前以钢管壁为支托,通过扭紧螺帽使其产生预拉力,然后与钢管壁焊接成一体,由拉杆预拉力对钢管壁和核心混凝土进行预压。

试验中的矩形钢管由4块厚度为5.5mm的钢板拼焊而成,拼焊前在设置约束拉杆的地方机械钻孔,孔径为22mm,以预留拉杆穿入孔道。加工时,尽可能保证钢管两端截面的平整,同时在钢管两端设有比截面4边各宽出30mm的盖板,盖板厚20mm。所有试件在浇灌混凝土前先将一端的盖板焊好,并将钢管竖立,混凝土从顶部灌入。对不同的试件,施工过程有一定差异,不设约束拉杆的试件,直接在钢管中浇注混凝土成型;设普通约束拉杆的试件,在浇注混凝土前,先在钢板预留孔道处穿入高强度螺栓,然后将螺栓螺杆通过垫板与钢管壁围焊连成一体,最后灌入混凝土成型;设预应力约束拉杆的试件,在浇注混凝土前,先在钢板预留孔道处插入直径为22mm圆钢,然后浇注混凝土,待混凝土强度达到一定值后,将圆钢拔出,预留出螺栓孔道,直到试验加载前穿入高强螺栓并通过扭矩扳手拧紧,对钢管壁和核心混凝土施加预压力。参照《JGJ82-91钢结构高强度螺栓的设计、施工及验收规程》,在本次试验中,对每个高强度螺栓施加的预拉力大小为155 kN。

试验用混凝土为C30商品混凝土,试件浇注完以后,采用自然养护办法,两三周后,发现混凝土沿试件纵向有大约0.5mm的收缩。在试件加载前1天,用丙烯酸酯结构胶将混凝土表面与钢管截面抹平,然后粘上另一盖板,以保证钢管和核心混凝土在受荷初期就能共同受力。在浇注混凝土制作试件的同时,浇注边长为150mm的混凝土立方体试块,与试件在同等条件下养护,试验开始当天按《GBJ81-85普通混凝土力学性能试验方法》进行试块立方体强度测试以获取混凝土的抗压强度fcu。钢材材料性质测试办法是:先将钢板做成3个标准试件,然后按《GB228-87金属拉伸试验方法》规定进行拉伸试验,由拉伸试验最终获得钢板的屈服强度(fy)、极限抗拉强度(fu)、弹性模量(Es)。此外,对高强度螺栓,还通过拉伸试验测定了螺栓螺杆的极限轴力Pu。各试件主要参数和材料性能见表1,试件形状与截面尺寸见图1。

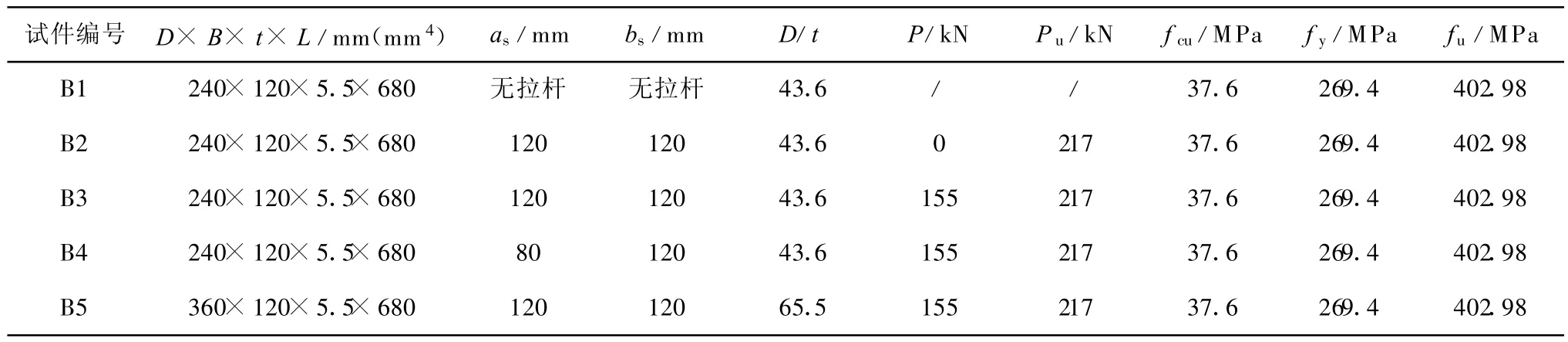
表1 试件几何参数及材料力学性能

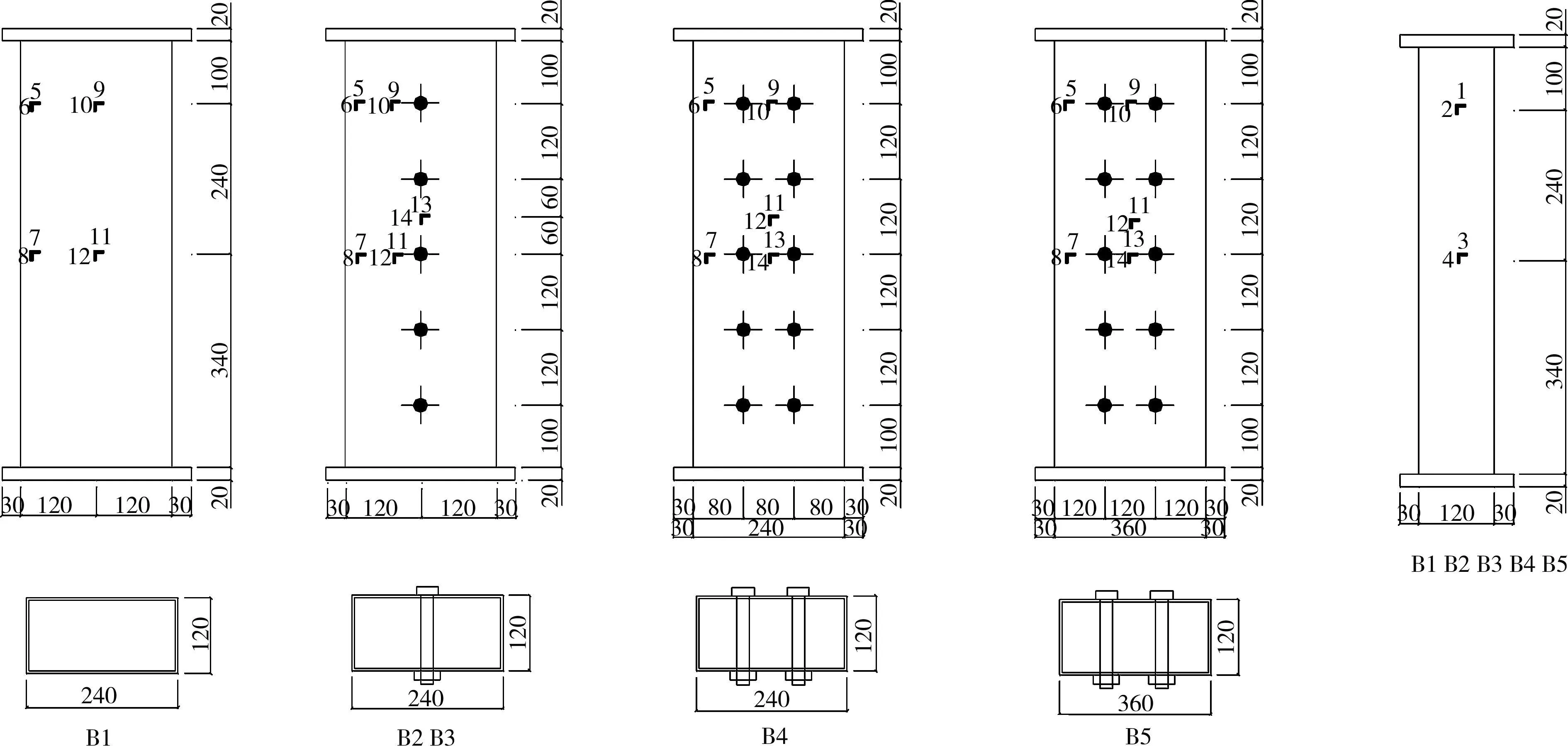
图1 试件形状与应变片布置图

1.2 加载与测试方法

试验在宁波大学土木工程实验室500 t长柱试验机上进行。试验前,先用打磨机将试件两端打磨平整,然后将试件置于试验机上,放置前在试件和试验机接触面上抹一薄层细砂,以保证试件加载时的垂直度;加载时,在试件顶面放置一块600mm×600mm×60mm钢板,钢板上立放500 t的压力传感器,以便于试验各项数据的同步采集,试验机荷载通过压力传感器和钢板传递给试件,试验加载装置见图2。为了考察约束拉杆设置后钢管壁表面不同位置的变形差异,在试件长、短边分别布置了一系列纵向和横向应变片,同时还沿试件纵向设置了两个位移计,以测试试件的荷载下的纵向总变形,各试件的测点布置见图1。

在试验正式加载前,先进行一级大约相当于20%极限荷载的预加载,以检查各仪器仪表正常运行情况。正常加载时,根据试验机自带压力传感器显示的荷载值控制加载速度,加载速度大约 100 kN/min。加载荷载、钢管壁应变以及试件两端的相对位移数据由DH 3816静态应变测试仪全程采集,采点频率为0.5次/s。试验时人工观察试件在加载过程中的各种试验现象。

图2 加载装置

2 试验结果与分析

2.1 试验现象与破坏形态

不带约束拉杆的B1试件在受荷初期,试件端部位移很小,试件基本处于弹性工作状态,随着荷载的增加,试件两端的相对位移增长速度加快,试件表现出弹塑性变形特征,当荷载增加到大约极限荷载的90%时,在试件短边沿纵向出现平行的滑移线,长边截面则出现斜向平行滑移线,随后试件长边加载端附近钢管壁屈曲外鼓,试件逐渐丧失承载力而发生破坏。带普通约束拉杆的B2试件在受荷初期也处于弹性工作状态,当荷载增加到大约极限荷载的40%左右,位于约束拉杆中部的钢管壁开始微鼓,构件变形增长速度加快,表现出明显的弹塑性变形特征,当荷载增加到大约极限荷载的90%时,加载端端部以及第1、2排螺栓中间部位钢管壁屈曲外鼓速度加快,试件随后达到极限承载力而破坏,破坏时试件短边钢管壁局部发生蜕皮现象。带预应力约束拉杆的B3试件在荷载小于40%的极限荷载以前,试件基本处于弹性阶段,随着荷载的增大,试件长边约束拉杆之间的钢管壁微鼓,当荷载达到极限荷载的90%左右,出现以螺栓为轴沿450线分布的放射状剪切滑移线,随后及第1、2排螺栓中间部位钢管壁屈曲外鼓加快,试件达到极限承载力而发生破坏,破坏时试件短边钢管壁出现蜕皮和屈曲外鼓现象。B4试件的破坏过程与B3试件基本相似,荷载达到极限荷载的90%左右时,长边横向约束拉杆之间的钢管壁屈曲外鼓,其中第1、2排螺栓中间部位钢管壁外鼓最为明显,试件随后达到极限承载力而发生破坏,破坏时截面短边也出现局部外鼓现象。B5试件在荷载小于40%的极限荷载以前基本处于弹性阶段,随后在试件长边靠近中部位置的2、3排和3、4排约束拉杆之间的钢管壁发生轻微鼓曲,此时短边钢管壁相对完好,当荷载增加到大约90%极限荷载时,试件长边的钢管壁表面出现蜕皮现象,长边约束拉杆之间的钢管壁外鼓速度加快,试件随后达到极限承载力而发生破坏,破坏时截面短边基本完好,未出现明显的外鼓现象。各试件的最终破坏形态见图3。

图3 试件的破坏形态

2.2 应变特点

图4给出了各试件钢管壁上不同位置处的荷载-纵、横向应变关系曲线。图中横坐标正方向代表横向应变,横坐标负方向代表纵向应变。从图4(a)中所测点的应变可以看到,不带约束拉杆的B1试件,在受荷初期,各点的纵、横向应变发展比较一致,但纵向应变发展较快;最大纵向应变达到钢管壁的屈服应变后,试件很快发生破坏,破坏时横向应变还处于较底水平,钢管对混凝土的约束作用没有充分发挥。从图4(b)可以看到,设置普通约束拉杆的B2试件,在受荷初期,各点的纵、横向应变发展也都比较一致,随着荷载的增大,应变增长速度出现差异,就纵向应变而言,截面长边端部点的应变发展最快,两排约束拉杆之间的纵向应变发展最慢,拉杆对钢管壁纵向变形的约束作用十分明显;就横向应变而言,应变最大点位于短边中部,由于拉杆的约束影响,截面长边的应变相对较小。与试件B1相比,试件B2在最大荷载后应变有平缓的水平发展段,延性大大提高。图4(c)带预应力约束拉杆试件B3的应变发展与试件B2大致相似,不同的是纵向应变最大值由截面长边端部位置转移至截面短边中部位置。与试件B3相比,试件B4仅改变了约束拉杆的横向间距,拉杆由单列变成了双列,从图4(d)中可以看出,由于约束拉杆间距的减小,试件B4横向应变最小的位置由截面长边端部转移至截面长边中部两排约束拉杆之间。试件B5与B4相比,截面长边尺寸发生了变化,截面长宽比由原来的2.0增加到3.0,从图4(d)中可以看到,由于截面长度的增加,约束拉杆间距增大,拉杆对长边钢管壁的横向变形约束减小,最大横向应变点位置由截面短边中点转移至截面长边两排横向约束拉杆之间。

2.3 承载力与变形特点

由试验得到各试件的轴向力-纵向位移曲线如图5所示。从图5(a)中可以看出,带约束拉杆的B2试件的承载力明显高于不带约束拉杆的B1试件;最大荷载后,B2试件的荷载-纵向位移曲线有很长的水平段,延性较好,而B1试件的荷载-纵向位移曲线则相对较陡,试件的承载能力衰减快,延性较差。从图5(b)中可以看出,带普通约束拉杆的B2试件和带预应力约束拉杆的B3试件的承载力和后期变形能力都大致相当,但后者对应于峰值荷载的变形(纵向位移)明显小于前者,表明拉杆预应力能提高构件的前期刚度,减小构件在正常使用荷载下的轴向变形。从图5(c)中可以看出,减小预应力约束拉杆的间距,对构件极限承载力影响不大,但可减小构件对应于峰值荷载的变形,提高构件的前期刚度。从图5(d)中可以看到,在截面宽度和拉杆数量不变的情况下,随着截面长宽比的增加,构件的承载能力提高,但是由于约束拉杆间距的增大,构件后期变形能力减小。

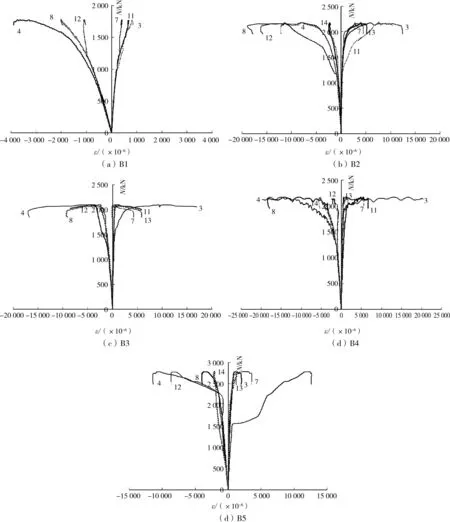
图4 钢管壁的荷载-纵、横向应变曲线

3 承载力计算探讨

目前国内外有关钢管混凝土的设计规范或规程较多 ,如欧洲 EC4(2004)、日本 AIJ(1997)、英国BS5400(2005)、美国 ACI(2005)和 AISC(2005)以及我国的 GJB 4142-2000、DBJ 13-51-2003以及CECS 159-2004等,这些规范或规程大都有专门针对圆钢管混凝土、普通方形或矩形钢管混凝土承载力设计计算方法的条文,为比较这些计算方法在进行带预应力约束拉杆矩形钢管混凝土短柱轴压承载力计算时的适用性和差异,选择EC4(2004)[17]、AIJ(1997)[18]、AISC(2005)[19]以及 GJB 4142-2000[20]和CECS 159-2004[21]中方法对本次试验试件的承载力进行了计算,计算时采用实测的材料强度,其中按GJB 4142-2000和CECS 159-2004方法计算时,混凝土轴心抗压强度取实测立方体抗压强度的0.76倍 ,采用 EC4(2004)、AIJ(1997)、AISC(2005)方法计算时,圆柱体抗压强度取实测立方体抗压强度的0.80倍,计算值与试验值的比较列于表2。结果显示,EC4(2004)、AIJ(1997)、AISC(2005)公式计算结果与B2、B3、B4、B5四个带约束拉杆试件的试验结果总体分别低 26%、20%、20%,GJB 4142-2000和CECS 159-2004 公式计算结果与B2、B3、B4、B5四个带约束拉杆试件的试验结果总体分别低10%、16%。因此,国内外现行规范或规程关于矩形钢管混凝土柱承载能力的计算方法都不适合于带约束拉杆矩形钢管混凝土柱承载能力的计算。进一步比较这些计算方法可以发现,除了GJB 4142-2000考虑了钢管对混凝土约束作用及其对构件承载力的有利影响外,其余规范或规程都没考虑这种影响,因此GJB 4142-2000计算结果与试验结果最为接近。建议在GJB 4142-2000计算方法基础上,引入考虑约束拉杆有利影响的承载能力提高系数β,来进行带约束拉杆的矩形钢管混凝土轴压短柱承载能力计算,具体公式如式(1)所示:

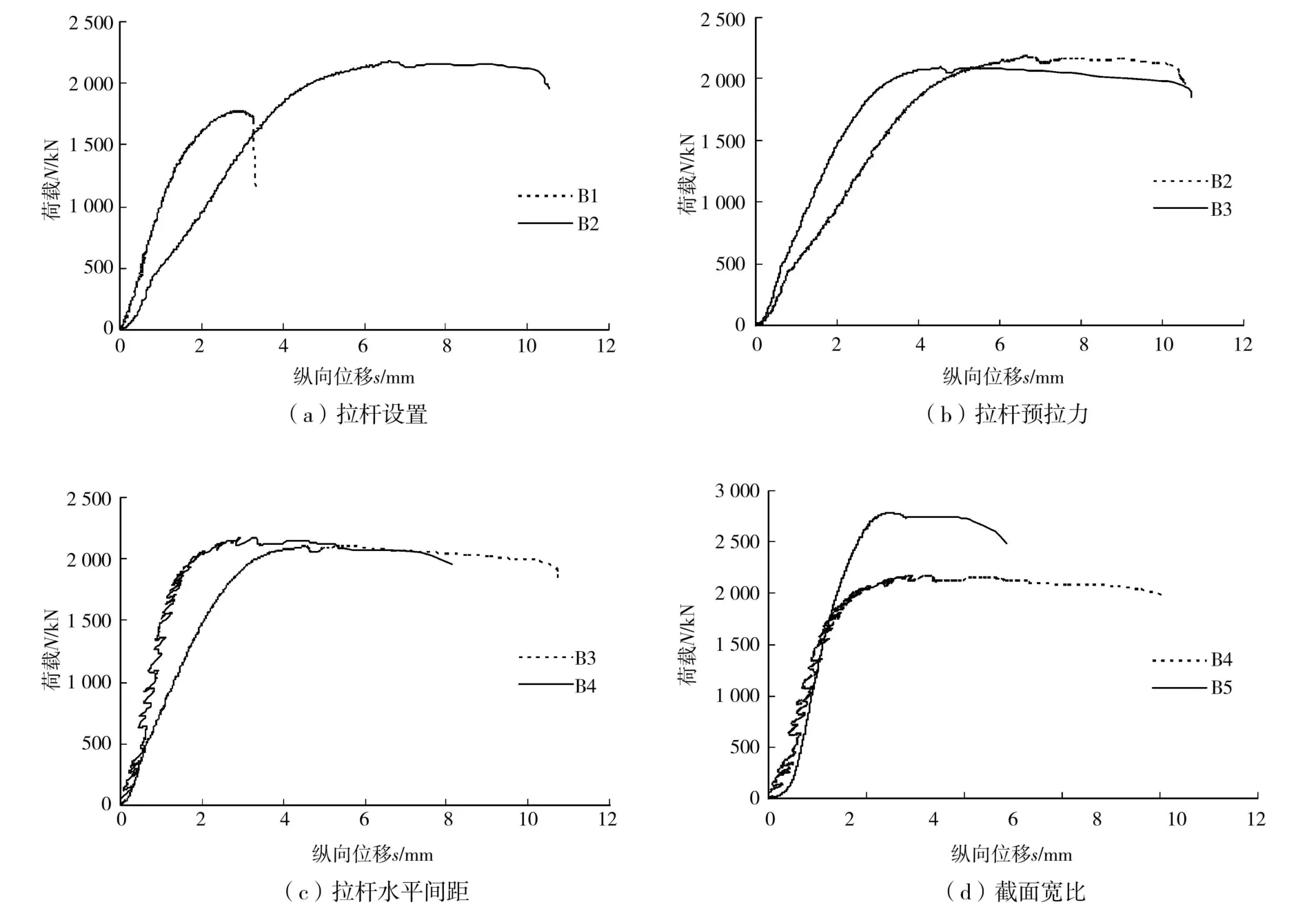
图5 试验参数对试件极限承载力和变形的影响

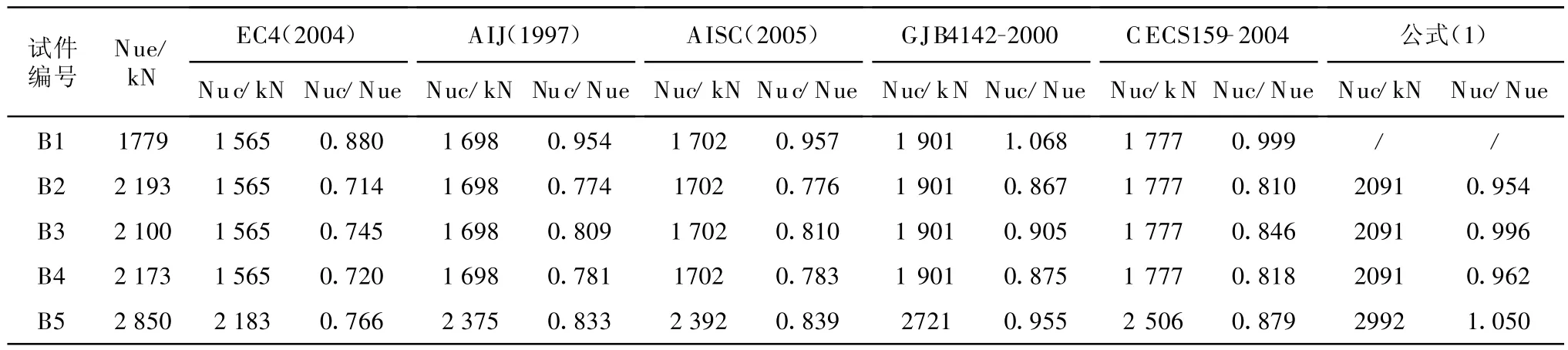
表2 承载力计算值和试验值比较

式中,β为考虑约束拉杆作用的承载能力提高系数,取β=1.1;Asc为钢管混凝土的横截面面积;fsc为钢管混凝土组合轴压强度设计值,按下式计算[20]:

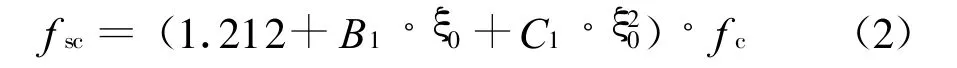
式中,B1和C1为计算系数,ξ0为截面约束效应系数设计值,分别用下式计算:

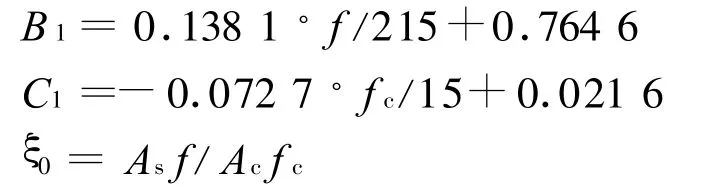
As和As分别为钢管和核心混凝土的横截面面积,f为钢材抗压强度设计值;fc为混凝土轴心抗压强度设计值。

利用公式(1)对文中4个带约束拉杆试件和文献[10]中7个带约束拉杆试件的承载力进行了计算,公式计算结果与试验结果对比的均值为0.990,标准差为0.030,计算结果与试验结果基本吻合。对于公式的适用范围,文献[22]的研究表明拉杆纵向间距对钢管壁局部屈曲性能有重要影响,因此在运用公式(1)时,建议约束拉杆纵向间距b s应符合b/3≤bs≤b/2的要求;另外该文和文献[15]的试验结果均表明,约束拉杆水平间距对构件极限承载力影响不显著,因此横向间距a s不大于截面宽度b即可。

4 结语

1)在矩形钢管混凝土柱长边沿纵向布置约束拉杆可显著提高构件的轴压承载力,改善构件的后期变形能力,提高构件的延性。

2)在此次试验条件下,带预应力约束拉杆的矩形钢管混凝土柱的承载能力和后期变形能力与带普通约束拉杆的矩形钢管混凝土柱大致相当,拉杆预拉力对构件承载力和极限位移影响不大,但能减小峰值荷载下的轴向变形,提高构件的前期刚度。

3)减小预应力约束拉杆的间距,对矩形钢管混凝土柱承载能力影响有限,但可有效减小构件最大荷载时的变形,提高构件前期刚度;在截面宽度和拉杆数量不变的情况下,随着截面长宽比的增加,构件承载力提高,但后期变形能力减小。

4)在规程GJB 4142-2000计算方法基础上,引入考虑约束拉杆作用的承载能力提高系数β,提出了带约束拉杆矩形钢管混凝土短柱轴压承载力的计算公式,公式的计算结果与试验结果基本吻合。

5)试验仅是对带预应力约束拉杆钢管混凝土柱受力性能和承载力计算方法的初步探索,拉杆强度、预应力水平等参数对构件受力性能和承载力计算的影响有待于进一步深入研究。

[1]SCHNEIDER S P.Axially loaded concrete-filled steel tubes[J].Journal of Structural Engineering,1998,124(10):1125-1138.

[2]UY B.Strength of short concretEfilled high strength steel box columns[J].Journal of Constructional steel research,2001,57(2):114-134.

[3]SAKINO K,NAKAHARA H,MORINO S,et al.Behaviour of centrally loaded concrete-filled steel-tubEshort columns[J].Journal of Structural Engineering,2004,130(2):180-188.

[4]韩林海,杨有福.矩形钢管混凝土轴心受压构件强度承载力的试验研究[J].土木工程学报,2001,34(4):22-31 HAN LIN-HAI,YANG YOU-FU.Study on axial bearing capacity of concrete-filled-steel-tubEcolumns with rectangular section[J].China Civil Engineering Journal,2001,34(4):22-31.

[5]王丹,吕西林.T形、L形钢管混凝土柱抗震性能试验研究[J].建筑结构学报,2005,26(4):39-44 WANG DAN,LvXI-LIN.Experimental study on seismic behavior of concrete-filled steel T-section and L-section columns[J].Journal of Building Structures,2005,26(4):39-44.

[6]MAO X Y,XIAO Y.Seismic behavior of confined squarECFT columns[J].Engineering Structures,2006,28(10):1378-1386

[7]LU F W,LI SP,SUN G J.A study on thebehavior of eccentrically compressed squarEconcrete-filled steel tubEcolumns[J].Journal of constructional Steel Research,2007,63(7):941-948.

[8]何振强,蔡健.带约束拉杆方形钢管混凝土偏压短柱的试验研究[J].华南理工大学学报:自然科学版,2006,34(2):107-111.HEZHENGQIANG, CAI JIAN.Experimental investigation into squarECFT stub columns with binding bars under eccentric loads[J].Journal of South China University of Technology:Natural SciencEEdition,2006,34(2):107-111.

[9]龙跃凌,蔡健.带约束拉杆L形钢管混凝土短柱轴压性能的试验研究[J].华南理工大学学报:自然科学版,2006,34(11):87-92 LONG YUE-LING,CAI JIAN.Experimental investigation into axial compressivEbehavior of L-shaped concrete-filled steel stub columns with binding bars[J].Journal of South China University of Technology:Natural SciencEEdition,2006,34(11):87-92.

[10]蔡健,何振强,陈星.带约束拉杆矩形钢管混凝土短柱轴压性能的试验[J].工业建筑,2007,37(3):75-80.CAI JIAN,HEZHEN-QIANG,CHEN XING.Experimental study on behavior of rectanglECFT stub column with binding bars subjected to axially loading[J].Industrial Construction,2007,37(3):75-80.

[11]蔡健,何振强.带约束拉杆方形钢管混凝土柱偏压性能[J].建筑结构学报,2007,28(4):25-35 CAI JIAN,HEZHENG-QIANG.Eccentric-loaded behavior of squarECFT columns with binding bars[J].Journal of Building Structures,2007,28(4):25-35.

[12]蔡健,孙刚.轴压下带约束拉杆L形钢管混凝土短柱的试验研究[J].土木工程学报,2008,41(9):14-20.CAI JIAN,SUN GANG.Experimental investigation on L-shaped concrete-filled steel stub columns with binding bars under axial load[J].China Civil Engineering Journal,2008,41(9):14-20.

[13]蔡健,龙跃凌.带约束拉杆矩形钢管混凝土的本构关系[J].工程力学,2008,25(2):137-143.CAI JIAN,LONG YUE-LING.ConstitutivErelationshiPof rectangular CFT column with binding bars[J].Engineeringmechanics,2008,25(2):137-143.

[14]陈曦,周德源.带约束拉杆矩形钢管混凝土轴压承载力分析[J].沈阳工业大学学报,2008,30(5):595-598.CHEN XI,ZHOU DE-YUAN.Analysis on axial strength of R-CFT stub column with unidirectional binding bars[J].Journal of Shenyang University of Technology,2008,30(5):595-598.

[15]蔡健,龙跃凌.带约束拉杆方形、矩形钢管混凝土短柱轴压承载力[J].建筑结构学报,2009,30(1):7-14.CAI JIAN,LONG YUE-LING,.Axial bearing capacity of squarEand rectangular CFT stub columns with binding bars[J].Journal of Building Structures,2009,30(1):7-14.

[16]陈曦,周德源.矩形钢管混凝土轴压短柱中采用不同混凝土材料模型的性能比较分析[J].建筑结构学报,2009,30(3):120-125.CHEN XI,ZHOU DE-YUAN.Comparison among axial behaviors of rectangular CFT stub column by adopting fivematerialmodels of concrete[J].Journal of Building Structures,2009,30(3):120-125.

[17]EC4.Design of steel and concretEstructures,Part-1:General rules and rules for buildings[S].Brussels:European CommitteEfor Standardization,2004

[18]AIJ.Recommendation for design and construction of concretEfilled steel tubular structures[S].Tokyo:Architectural InstitutEof Japan,1997

[19]Aisc-Lrfd Specification for structural steel buildings[S].Chicago:American InstitutEof Steel Construction,2005.

[20]中国人民解放军总后勤部.GJB 4142-2000战时军港抢修早强型组合结构设计规程[S].2001.

[21]CECS 159:2004矩形钢管混凝土结构技术规程[S].北京:中国计划出版社,2004.

[22]蔡健,何振强,金雪峰.带约束拉杆方形钢管混凝土轴压柱局部屈曲性能[J].工程力学,2007,24(5):169-175.CAI JIAN,HEZHEN-QIANG,JING XUE-FENG.Local buckling of squarEconcrete-filled steel tubular column with binding bars under axial loading[J].Engineeringmechanics,2007,24(5):169-175.