一种考虑软件补丁的软件可靠性模型研究
2010-08-08付方智沈元隆
付方智,沈元隆
(南京邮电大学 电子科学与工程学院,江苏 南京 210003)
从1972年至今,为了研究软件可靠性,已经提出一百多种模型,但这其中大部分模型主要是从消除软件中的错误数的角度来研究软件的可靠性模型。而另一种现象也逐渐被重视起来,就是一种软件在发布后,软件产品的可靠性伴随着时间增长,而错误数并没有纠正的情况下,软件的可靠性也得到了改善。为了描述这种软件产品可靠性的增长,2008年PankajJalote和Brendan Murphy从用户角度,针对软件产品销售后可靠性增长的现象提出一种关于软件产品的可靠性预计模型[1]。但是,在 Pankaj Jalote和Brendan Murph提出的模型中,其假设在某些方面过于严格,特别是所提出的模型中忽视了软件补丁的作用。而现在软件补丁的作用越来越大,因而软件的补丁不能被忽视了。本文全面分析了实际情况,提出了考虑软件补丁的关于软件产品的软件可靠性增长模型。
1 原始的关于软件产品的软件可靠性增长模型
1.1 基本假设与公式
2008年Pankaj Jalote和Brendan Murphy提出的一种关于软件产品的可靠性增长模型[1],假定如下:
(1)假定软件销售出去以后,没有新的版本发布出来,不考虑软件的补丁的问题,认为补丁的影响微乎其微。
(2)假定用户初始的失效率为(λ0+λf),稳定时的失效率 为 λf。
(3)假定可以通过软件产品技术支持服务,获得每个月的产品销售量与每个月的总的失效总数。
(4)针对用户,软件的失效率以常数每个月来进行衰减,并且 αi+1为 αi的 k倍(k>1),直到它达到稳定的状态。
失效率的定义:假定用户安装了N套某种软件产品,从安装时刻开始,经历了T的时间间隔,总的失效数为 F,则:

从用户的角度,给一个失效率公式:

基于以上的假定,可以得出如下模型:
假定:第一月卖出 N1套,第二个月卖出 N2套,…,第i个月卖出 Ni套;令这种软件的暂态的失效率是 λ0,每个月软件衰退率为α,稳态的失效态是λf,由此可以得到每个月的总的失效数Fi:
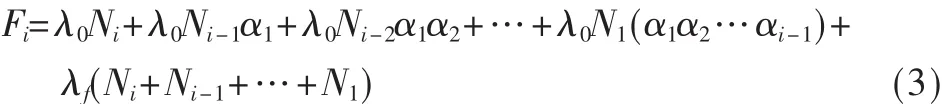
由于α1=α,则可以得到:

将式(4)代入式(3)得:
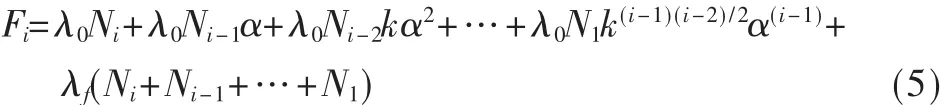
由于任何一个月的故障率都是不可能增加的,故k的限定条件为:

1.2 模型的参数估计
利用收集到每月的失效总数和每月的产品销售数,并采用最大拟然法或者最小二乘法来对 λ0、λf、α、k进行估计,以改进模型。然后,软件产品公司再利用估计的参数和模型,对某种软件产品进行可靠性预测,从而根据预测进行对产品的改进。利用最小二乘法对于模型参数的估计公式如下:
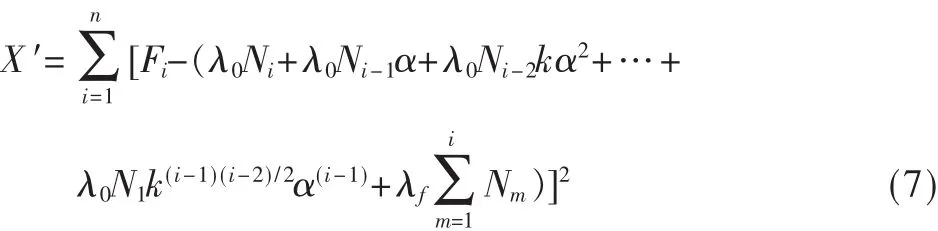
2 考虑软件补丁的关于软件产品的软件可靠性增长模型
2.1 新模型的假设与基本公式
基于前面的分析,本文重新修正2008年Pankaj Jalote和Brendan Murphy提出的关于软件产品的软件可靠性预计模型的假设,并提出改进的模型,并称其为FP模型。
FP模型是对改进的模型考虑了补丁之后的模型,并认为补丁虽然可以纠正软件中的错误,但是同样会带来新的错误,因此引进2个新的参数β、γ,其假设如下:
(1)假定软件销售出去以后,没有新的版本发布出来,补丁及时发布,用户能及时安装和使用,而新的补丁安装后会带来新的错误。
(2)假定用户初始的失效率为 λ0+λf,稳定时的失效率 为 λf。
(3)假定可以通过软件产品技术支持服务获得每个月的产品销售量与每个月的总的失效率。
(4)针对用户,由于考虑到了补丁的影响以及会带来新的问题,所以软件的每个月失效率为 αi,直到它达到稳定的状态。
根据上述假设可以得到此模型的失效率公式:

其中λ为时间。

将原模型的公式修正为:
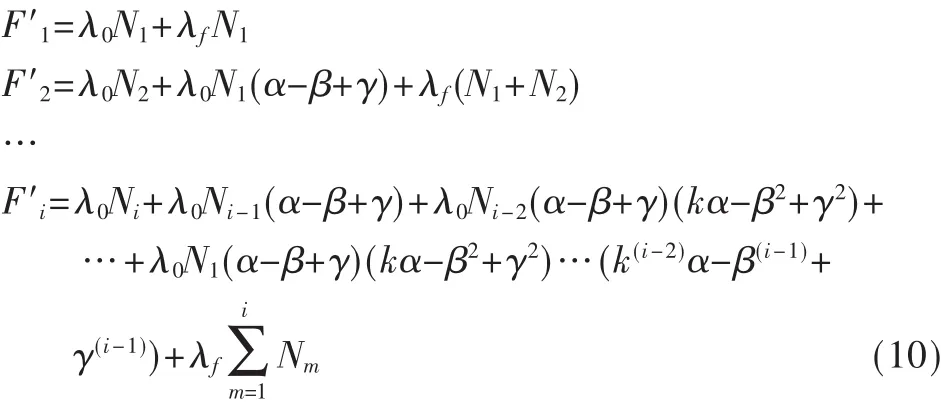
2.2 FP模型的参数估计
利用收集的每月的失效总数和每月的产品销售数,并采用最大似然法或者最小二乘法来对 λ0、λf、α、β、γ、k进行估计FP改进模型,软件产品公司再利用估计的参数和模型,对某种软件产品进行可靠性预测,从而根据预测进行对产品的改进。利用最小二乘法对模型参数的估计公式如下:
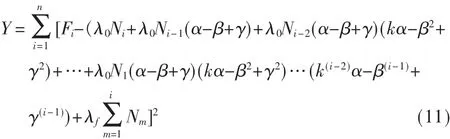
3 实例仿真
本实例仿真数据是来源于2008年Pankaj Jalote和Brendan Murphy在ACM Trans发表的文献[1]。仿真数据如表1所示。
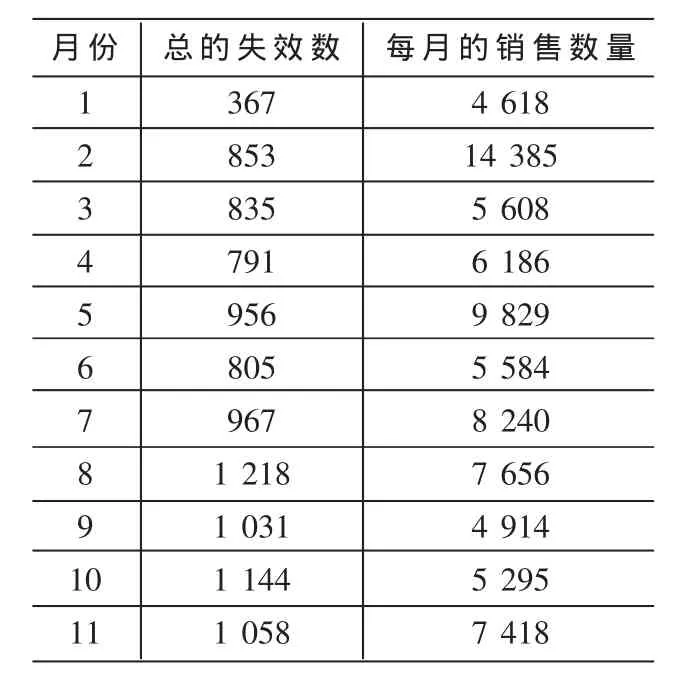
表1 某公司每月销售情况和每月失效总数
通过数值方法求得FP模型和原模型的参数值如表2所示。

表2 FP模型和原模型的参数值
3.1 图形仿真
用Matlab 7.1仿真FP模型和原模型,仿真结果如图1所示。

图1 Matlab 7.1仿真图
从图1可以看出,改进的模型比原来的模型更接近实际的数据。
3.2 模型的常用预测能力比较
误差平方和SSE[2]用来描述累计失效数的观测值与预测值之间的距离,定义如下:

在式(12)中,n表示实效数据集中失效样本的数量,yi表示到时间ti为止累计故障数的实测值,ti)表示到时间ti为止累计故障数的估计值。
SSE越小,则表示曲线的拟合能力越好[3]。由表3可知,改进的FP模型在预测能力上优于原来的模型。

表3 两种模型的常用预测能力参数AE比较
通过分析和研究原始的关于软件产品的软件可靠性预计模型,考虑到软件补丁的作用不能忽视,提出了软件发布后的软件可靠性模型——一种考虑软件补丁的软件可靠性模型。本文首先分析了原模型的假设和软件补丁对软件可靠性的影响,提出修订的假设条件,并由假设条件推出改进的FP模型,然后对改进的FP模型的参数估计展开讨论,并得到相应的函数表达式。利用最小二乘法求得模型参数,再通过仿真实验对原始的关于软件产品的软件可靠性预计模型和改进的FP模型进行分析比较,可以得出改进的FP模型的预测精度比原始模型要高,并且其拟合效果都要优于原始模型。
[1]JALOTE P,MURPHY B.Post-release reliability growth in software products[J].ACM Transactions on Software Engineering and Methodology(TOSEM), 2008,17(4).
[2]ZHANG Xue Mei, TENG Xiao Lin, PHAM H.Considering fault removal efficiency in software reliability assessment[J].IEEE Transactions on Systems, Man, and Cybernetics-PartA:Systems And Humans, 2003,33(1):114-119.
[3]赵靖,刘宏伟,崔刚,等.考虑测试与运行差别的软件可靠性增长模型[J].计算机研究与发展,2006,43(3):503-508.
