基于双螺旋桨差动调节的双体船航向智能控制研究

刘 杨，王 莹

(1.哈尔滨工程大学 自动化学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

近年来，双体船由于良好的操纵性、阻力峰不明显、装载量大等特点，在当今船舶行业得到了广泛的关注。本文根据双体船采用双螺旋桨作为其动力系统，提出一种基于双螺旋桨差动调节的双体船航向智能控制方法。通过引入航向误差检测环节、系统辨识环节和模糊控制，控制双体船航向运动。仿真结果表明，本文所设计的双螺旋桨差动调节航向智能控制系统控制效果良好，对海情的变化具有较强的适应能力。

1 双体船航向运动非线性模型

对于在水面内运动的双体船，在预定的航线上做小偏差运动时，纵向与横向运动耦合作用不大，可认为其纵向运动与横向运动相互独立，其横荡和首摇运动模型如式(1)所示：

其中，Yd和 Nd分别为海浪、海风及海流等扰动形成的干扰力和干扰力矩；Iz为双体船O-xy面绕Oz轴的转动惯量；θ为偏航首摇角度；v为横荡速度；M为双体船质量。

对模型式(1)进行简化处理，将由舵角产生的控制力和控制力矩改为由双螺旋桨差动形成的控制力和控制力矩代替，另外考虑在静水条件下，忽略海浪、海风和海流产生的扰动力、扰动力矩。则可描述为：

其中，YL、NL分别为双螺旋桨转速差异引起的横荡力、首摇力矩系数；Δω为双螺旋桨的转速差值。

2 双螺旋桨动力学模型

由于双体船宽度比一般船舶要宽，吃水也较一般船舶浅，所以根据其特点，采用了双螺旋桨推进系统。螺旋桨的动力学特性可表示为：

式中：ρ为水的密度；D为螺旋桨桨径；KQ为螺旋桨阻力系数；KT为螺旋桨推力系数；ω为螺旋桨转速。

若2个螺旋桨转速不同，则2个螺旋桨的推力不同，从而能够进行船体航向的调整，其产生的推力与航速的关系如下：

则相对艏摇，2个螺旋桨形成的控制双体船航向的控制力矩有如下关系：

其中，V为船的速度；L为两螺旋桨产生艏摇力矩对应的力臂；FL1为螺旋桨1产生的推力；FL2为螺旋桨2产生的推力。

3 控制系统设计

双体船航向智能控制系统如图1所示。两个螺旋桨是两个相互独立的控制机构，双螺旋桨分配单元包含双螺旋桨智能优化分配规则。在系统运行过程中，模糊控制器计算出所需的扶正力矩值，双螺旋桨分配单元根据该值计算出所需的两个螺旋桨的转速。

图1 双体船航向智能控制系统框图

(1)定义输入输出变量

本文设计的双体船航向模糊控制器，根据自动舵的工作原理，通过传感器测量可以得到双体船的航向角，因此可以选择航向角偏差Δψ作为模糊控制器的输入。另外，为了反映偏差的变化趋势，模糊控制器的输入还应加上航向角偏差的变化率。模糊控制器的输出为双螺旋桨所需的扶正力矩值。模糊控制器如图2所示，E为航向角误差；EC为航向角误差变化率；U为控制器的输出量；ke、kec为量化因子；ku为比例因子。

图2 模糊控制器输入输出示意图

(2)输入输出变量的模糊化

对模糊控制器的输入和输出进行模糊化处理，选择输入输出变量的模糊子集为：

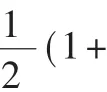
由于高斯型隶属函数的平滑性较好，概念较精确，所以本文中的模糊隶属函数均采用高斯型函数，如图 3、图 4、图 5所示。

4 系统仿真及结果分析

为了检验本文所设计的智能控制系统是否可以有效地提高航向控制效果、节约系统能耗，本文对系统进行仿真，如图6所示，所用双体船的主要参数：排水量为2 379 t，水线长为 57.58 m，水线面积为 175.87 m2，下潜体半径为2.286 m，支柱长度为57.58 m，浮心到重心的垂向距离4.63 m，支柱最大厚度为2.03 m，纵稳心高为8.44 m，下潜体长度为73.06 m，潜体浮心距离主体首端为35.2 m，船体吃水高度为7.62 m，纵摇惯性半径为15.88 m，设计航速为 18 kn。

图3 航向角偏差E的隶属度函数曲线

图5 控制量U的隶属度函数曲线

图6 航向模糊控制系统仿真曲线

为了进行有效地对比，本文还对该双体船在相同海情的航向PID控制系统进行了仿真，如图7所示。从仿真结果来看，当海情发生变化时，由航向PID控制的效果明显变差，且舵角幅度变大，增大了能耗。而本文设计的模糊控制系统在重新辨别模型、优化参数后能较好地适应海情变化，控制效果良好。由于模糊控制算法具有较强的全局寻优能力，而PID算法对参数初值的选取十分敏感，极易陷入局部最优，导致寻优失败。

图7 航向PID控制系统仿真曲线

本文设计了基于双螺旋桨差动调节的双体船航向智能控制系统，通过航向偏差检测环节判断海情是否发生变化。若海情发生变化，则通过系统辨识环节得到双体船航向运动的数学模型，并在该模型的基础上运用模糊控制算法，最后将得到的参数赋予实际的航向保持系统。仿真结果表明与PID控制系统相比，该系统对于海情变化具有较好的自适应能力。该系统简单易于实现，具有工程应用价值。

[1]LEE T H，LAM H K，LEUNG F H F，et al.A practical fuzzy logic controller for the path tracking of wheeled mobile robots[J].IEEE Control Systems Magazine， 2003，23(2):60-65.

[2]李殿璞.船舶运动与建模[M].北京:国防工业出版社，2008.

[3]顾树生，平力.模糊控制系统稳定性分析及控制其设计[J].控制与决策，1991(3):178-183.

[4]王守臣，徐颢.用多元逻辑电路实现模糊自组织控制器[J].电子学报，1998，26(5):63-65.

[5]吴梵，陈志坚，刘巨斌，等.小水线面双体船在波浪中的水动力计算[J].船海工程，2004，26(1):17-21.