平面P波在饱和半空间中凹陷地形周围的散射规律

巴振宁，梁建文，LEE V W

(1. 天津大学建筑工程学院，天津 300072；2. 南加州大学土木工程系，洛杉矶 CA90089-2531)

凹陷地形作为最常见的局部场地之一，其对地震动的显著影响已在多次地震观测和震害调查中得以证实．20世纪 70年代初，Trifunac[1]开创性地给出了平面 SH波在半圆凹陷周围散射二维问题的精确解，并研究了波在凹陷周围的散射规律．随后，国内外多位学者对该问题进行了研究．求解方法主要有解析法[1-2]和数值法[3-4]．解析法主要有波函数展开法；数值法主要包括有限差分法、有限元法、边界元法、离散波数法、波源法和边界法等．

然而，实际场地常常是饱和两相介质．基于 Biot饱和土中波的传播理论[5]，Lin等[6]研究了入射平面P和SV波在饱和半空间表面的反射问题．文献[7]采用波函数展开法给出了平面 P波在饱和半空间中凹陷地形周围散射的解析解，但对波在凹陷周围的散射规律还有待进一步分析．

另外，值得指出的是，文献[6]在实验数据基础上，引入了临界孔隙率的概念，模型更接近实际情况，也使得研究者有可能考察孔隙率接近临界孔隙率状态下饱和局部场地对波的散射规律．

文献[8]采用波函数展开法给出了平面 SV波在饱和半空间中凹陷地形周围散射的解析解，并对波在凹陷周围的散射规律(包括孔隙率接近或等于临界孔隙率状态下波的散射规律)进行了深入研究．本文则在文献[8]的基础上，进一步研究了平面 P波在饱和半空间中凹陷地形周围的散射规律．

1 模 型

图1所示为饱和半空间中一圆弧形凹陷地形，圆心位于 o1，半径 b，弧深 h．根据两相饱和多孔介质的Biot理论，一圆频率为ω的平面 P1波以角度θα1入射，其波势函数可以表示为

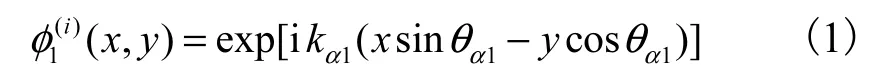
如果不存在凹陷地形，入射 P1波在饱和半空间自由表面将产生 1个反射 P1波、1个反射 P2波和 1个反射 SV 波．在极坐标系 r1-θ1下，P1、P2和 SV 波的波势函数可分别表示为Fourier-Bessel级数，即

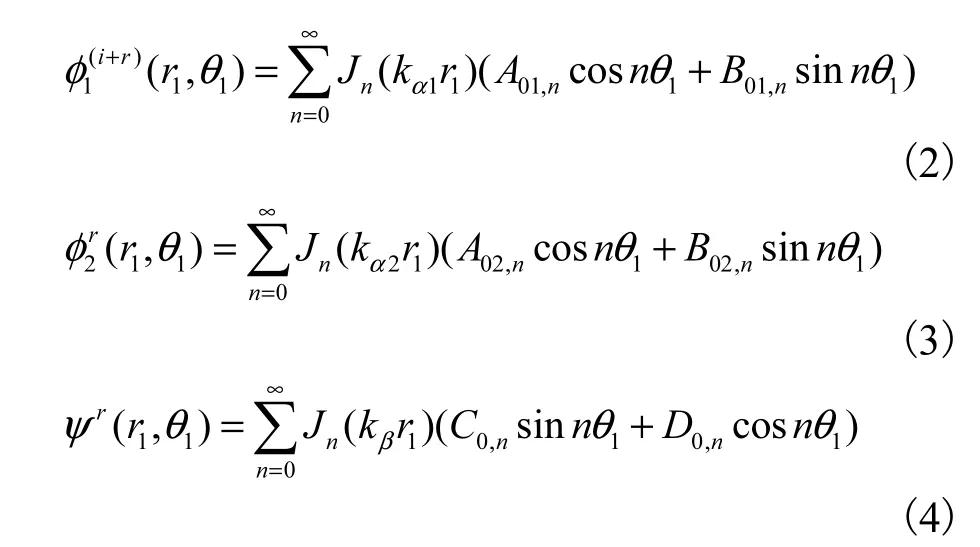
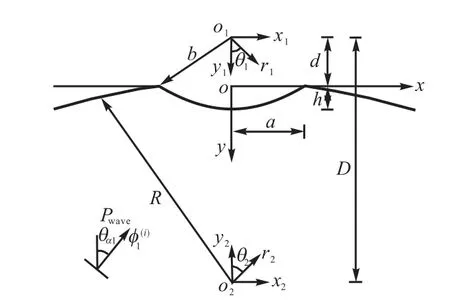
图1 饱和半空间中凹陷模型Fig.1 Model of canyon in saturated poroelastic half-space

由于凹陷地形的存在，在半空间中将会产生如下散射波，其Fourier-Bessel级数可分别表示为

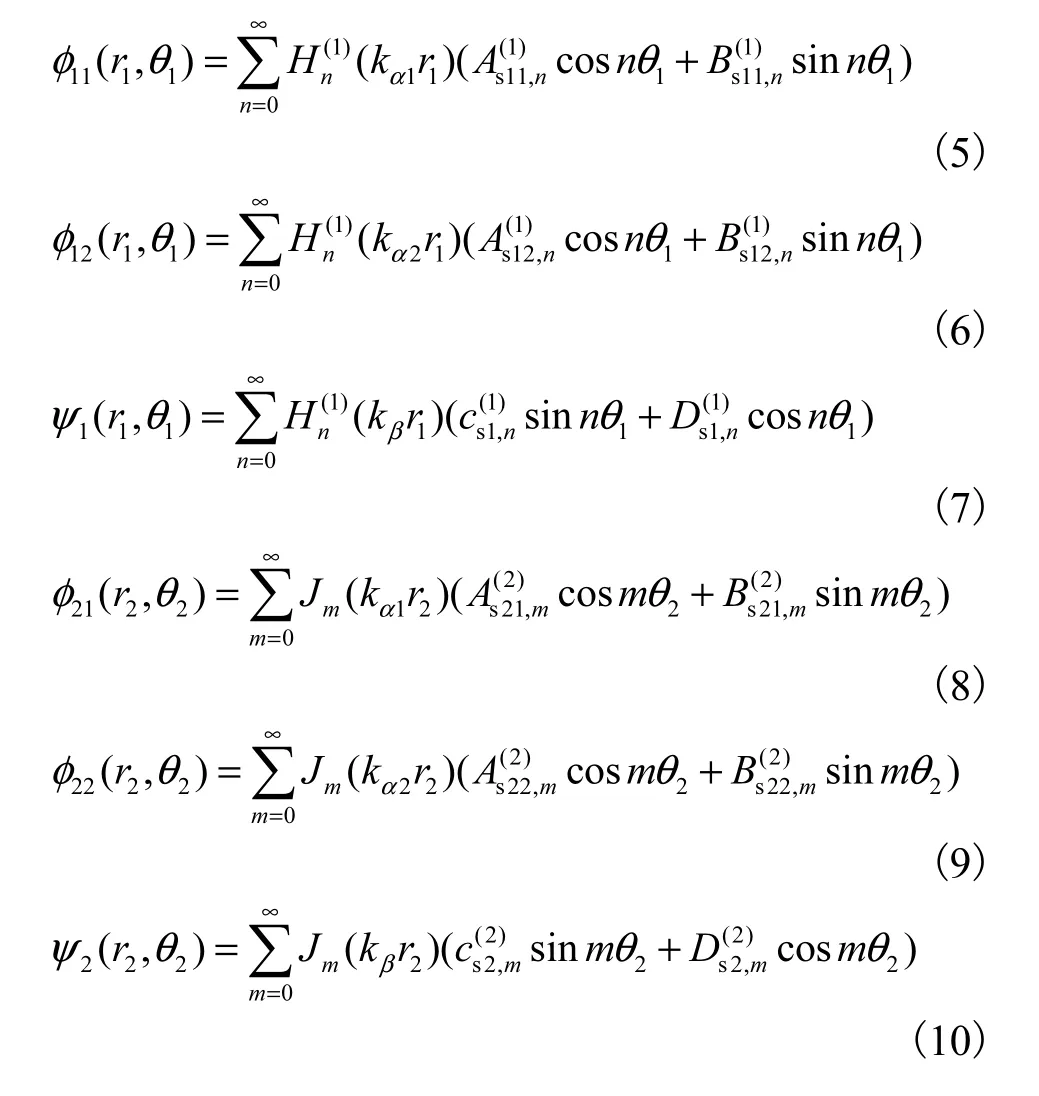
式中mJ和分别为第一类 Bessel函数和 Hankel函数．由此，半空间中总的波势函数可表示为

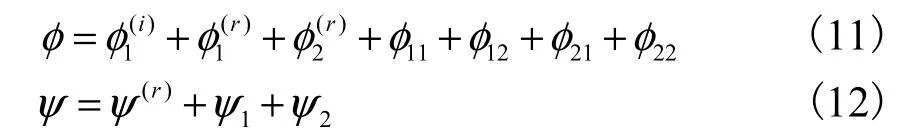
边界条件为：透水时，

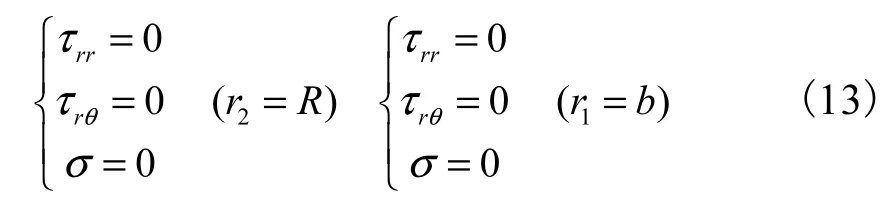
不透水时，

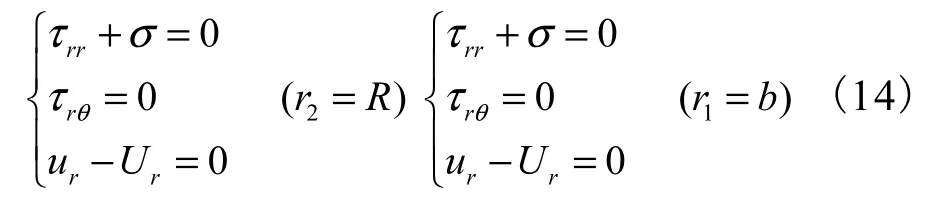
由两相饱和多孔介质中位移和应力在平面应变问题中的极坐标形式[8]引入边界条件，就可以求出式(5)～(10)中的所有系数，然后求得凹陷地形和附近地表的位移以及孔隙水压．

2 数值结果与散射规律分析

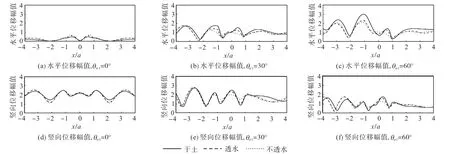
图2 干土、透水、不透水情况地表位移幅值比较(η＝1.0, n＝0.3, ν＝0.25)Fig.2 Surface displacement of dry poroelastic，drained saturated poroelastic，and undrained saturated,poroelastic half-spaces(η＝1.0, n＝0.3, ν＝0.25)

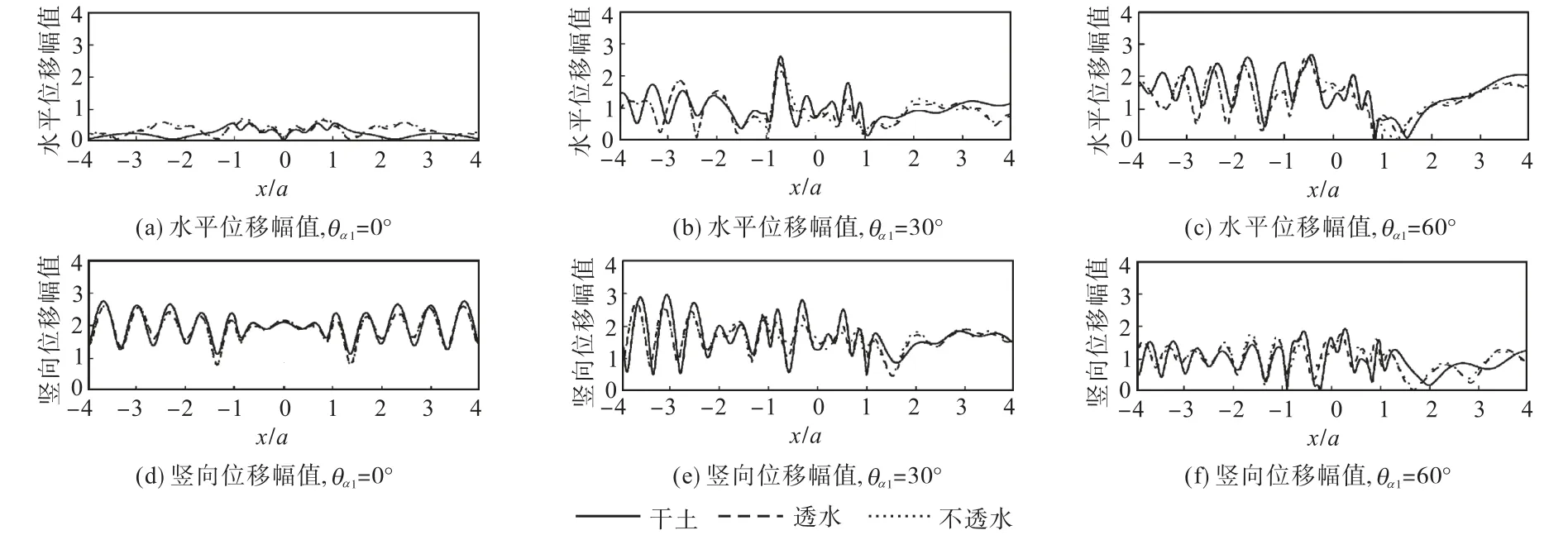
图3 干土、透水、不透水情况地表位移幅值比较(η＝3.0, n＝0.3, ν＝0.25)Fig.3 Surface displacement of dry poroelastic，drained saturated poroelastic，and undrained saturated poroelastic half-spaces(η＝3.0, n＝0.3, ν＝0.25)

定义无量纲频率η =2a / λβ．式中：a为凹陷地形的半宽；λβ为半空间中剪切波的波长．在下面的数值计算中，凹陷地形埋深h/a=0.5；取饱和半空间介质特性[6]：临界孔隙率 ncr＝0.36，土骨架临界体积模量Kcr=200,MPa，土颗粒体积模量 Kg＝36,000,MPa，流体体积模量 Kf=2,000,MPa，土颗粒质量密度ρg＝2,650,kg/m3，流体质量密度ρf=1,000,kg/m3，孔隙率n＝0.1、0.3、0.34和 0.36，相应土骨架体积模量Kdry=26,055,MPa、6,167,MPa、2,189,MPa 和 200,MPa，泊松比ν＝0.2、0.3和0.4．

图2～图 4分别给出了入射波 P1频率η=1.0、3.0和 5.0三种情况下，半空间介质孔隙率 n＝0.3、泊松比ν=0.25，入射角度θα1＝0°、30°、60°（因篇幅所限，未给出1αθ=85°的结果)，干土情况、透水情况和不透水情况对凹陷地形附近地表水平和竖向位移幅值的影响．图中的地表位移幅值已由入射波的位移幅值正规化．可以看出，图2(η =1.0)中对应干土情况的地表位移幅值与文献[2]单相弹性半空间结果相同．从图 2～图 4还可以看出，透水情况和不透水情况地表位移幅值比较接近，说明边界渗透条件对地表位移幅值的影响并不是很大．相反，饱和情况(透水或不透水)与干土情况的差别却很大：当波掠入射时，干土情况地表位移幅值远大于饱和情况地表位移幅值；饱和情况与干土情况的地表位移出现相位漂移，饱和情况地表位移波长相对较大，这与SV波入射情况[8]相同，是由于波在凹陷地形附近的干涉造成的．对于掠入射情况，可以观察到在波的入射端(x/a＜−1)出现驻波现象．

图4 干土、透水、不透水情况地表位移幅值比较(η＝5.0, n＝0.3, ν＝0.25)Fig.4 Surface displacement of dry poroelastic，drained saturated poroelastic，and undrained saturated poroelastic half-spaces(η＝5.0, n＝0.3, ν＝0.25)

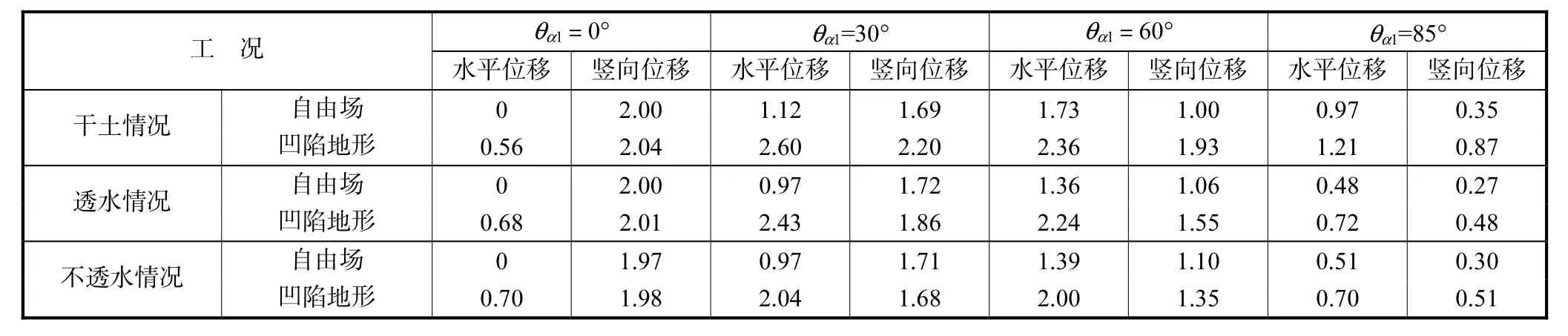
表1 自由场和凹陷地形分别引起的最大地表位移幅值比较(η＝3.0)Tab.1 Maximal normalized surface displacement amplitudes due to free field and canyon(η=3.0)

为了进一步比较干土、透水情况和不透水情况下波在凹陷地形附近散射规律的差别，分别给出了η＝3.0和5.0两种情况下自由场和凹陷地形分别引起的最大地表位移幅值比较，见表 1和表 2．可以看出，透水情况和不透水情况的自由场地表位移幅值比较接近，而饱和情况和干土情况的自由场地表位移幅值相差较大，尤其是在波入射角度较大情况(如θα1=85°)，这也是图2～图4中透水情况和不透水情况地表位移幅值比较接近、饱和情况(透水或不透水)与干土情况的差别比较大的主要原因．从表1、表2还可以看出，当波垂直入射时(θα1=0°)，凹陷地形的存在会引起水平位移，且在最大地表水平位移幅值中，不透水情况最大，透水情况次之，干土情况最小．说明不透水情况下波型转换最显著，透水情况次之，干土情况最少．随着入射角度的增大(θα1=30°、60°和85°)，干土情况下凹陷地形引起的最大地表位移幅值大于饱和情况下引起的最大地表位移幅值．

图5和图6分别给出了透水和不透水情况下，半空间介质泊松比ν=0.25，入射波 P1频率η=1.0、3.0和5.0，入射角度θα1=45°，分别对应孔隙率 n=0.1、0.3、0.34和 0.36(临界状态)情况的凹陷地形附近地表水平和竖向位移幅值．可以看出，当入射频率较低时，随着孔隙率的增大，水平位移幅值逐渐减小，竖向位移幅值则逐渐增大，这主要是由其自由场决定的；当入射频率较高时，凹陷地形引起的散射场起主导作用，随着孔隙率的减小，地表位移幅值逐渐增大．当孔隙率较低时，边界渗透条件对地表位移幅值的影响很小，而当孔隙率较大时，边界渗透条件的影响则不可忽视：不透水情况下，水平和竖向地表位移幅值的峰值均相对较大；这与 SV 波入射情况[8]有着相同的结论．从图中还可以看出，随着入射频率的升高，孔隙率的影响逐渐增大；不透水情况下孔隙率的影响相对较大．

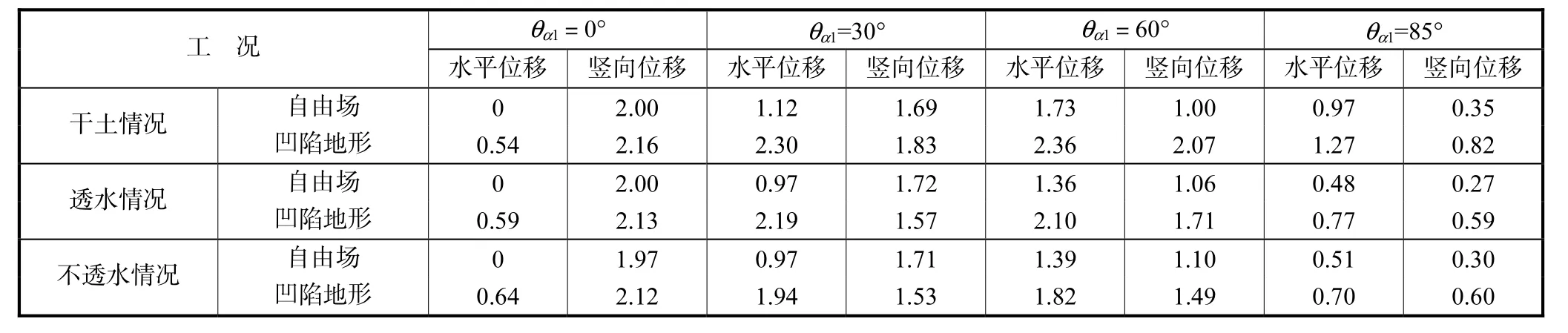
表2 自由场和凹陷地形分别引起的最大地表位移幅值比较(η＝5.0)Tab.2 Maximal normalized surface displacement amplitudes due to free field and canyon(η=5.0)

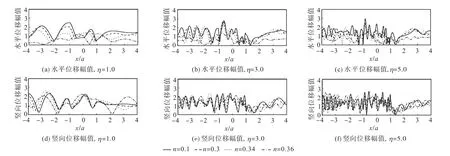
图5 孔隙率对地表位移幅值的影响(透水情况, θ α1 =45°,ν=0.25)Fig.5 Normalized surface displacement for different porosities(drained case, θ α1 =45°,ν=0.25)

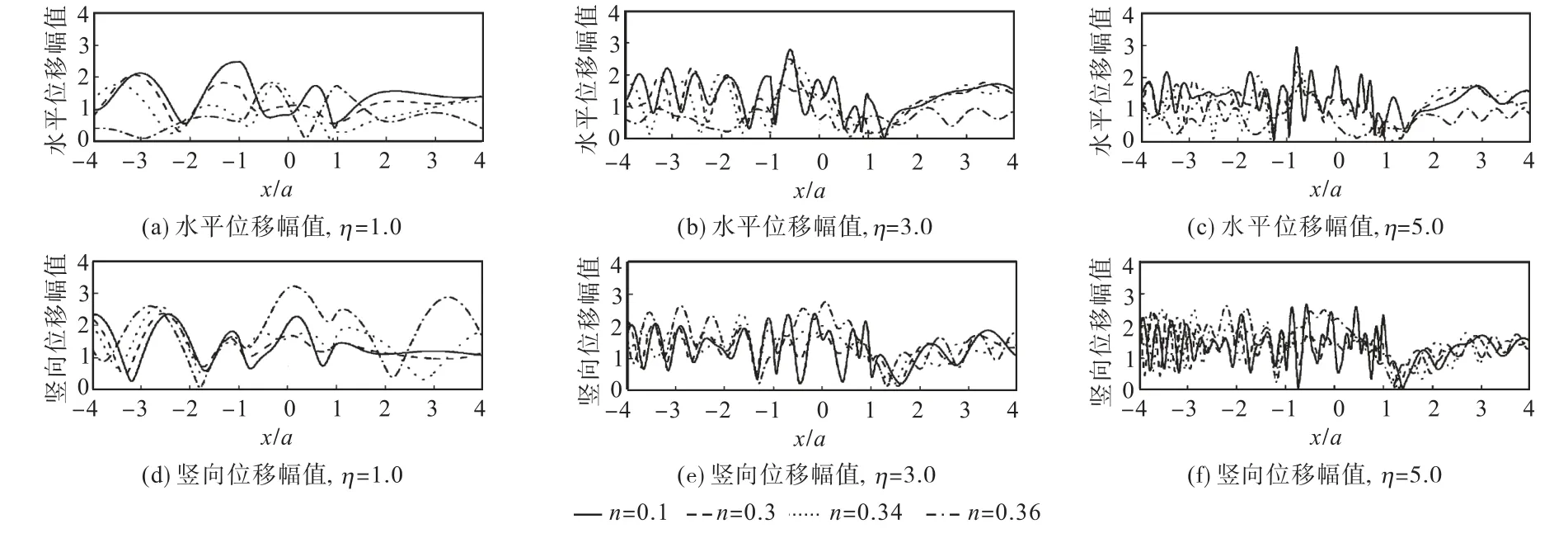
图6 孔隙率对地表位移幅值的影响(不透水情况, θ α1 =45°,ν=0.25)Fig.6 Normalized surface displacement for different porosities(undrained case, θ α1 =45°,ν=0.25)

图7 和图8分别给出了透水和不透水情况下，半空间介质孔隙率 n=0.3，入射波 P1频率分别为η=0.25、1.0、3.0 和 5.0，入射角度θα1=45°，分别对应泊松比ν=0.2、0.3、0.4情况的凹陷地形附近地表水平和竖向位移幅值．可以看出，随着泊松比的增大，水平位移幅值逐渐减小，竖向位移幅值则逐渐增大，这主要是由其自由场决定的．泊松比较小时，边界渗透条件对位移幅值的影响较大；泊松比较大时，边界渗透条件对位移幅值的影响较小，这与 SV波入射情况[8]有着相同的结论．从图中还可以看出，随着入射频率的升高，泊松比的影响逐渐增大．

图9～图 11分别给出了半空间地表和凹陷地形表面孔隙水压力(不透水情况)的分布情况．计算参数为：孔隙率 n=0.1、0.3和 0.36，半空间介质泊松比ν=0.25，入射角度θα1=0°、30°、60°，入射波 P1频率η=1.0、3.0和5.0．图中的孔隙水压幅值已由入射波的应力幅值正规化．从图中可以看出，当孔隙率较小时，孔隙水压幅值较小但空间变化比较剧烈；随着孔隙率的增大，孔隙水压逐渐增大但空间变化逐渐平缓．这是因为孔隙率越大，土骨架越软，则孔隙水承担越多的能量，孔隙水压自然也越大；同时孔隙率越大，孔隙水越多，孔隙压力变化也就越平缓．当孔隙率达到临界状态时，土骨架模量非常小，激励能量主要由 P1波承担[6]，孔隙水压显著增大，与 SV 波入射情况[8]差别很大(SV波入射时能量主要由 S波和 P2波承担[6]，而S波不产生孔隙水压)．从图中还可以看出，当入射频率较高时，孔隙水压幅值较大且孔隙水压的空间变化比较复杂，这说明频率较高的波更易激起孔隙水压．

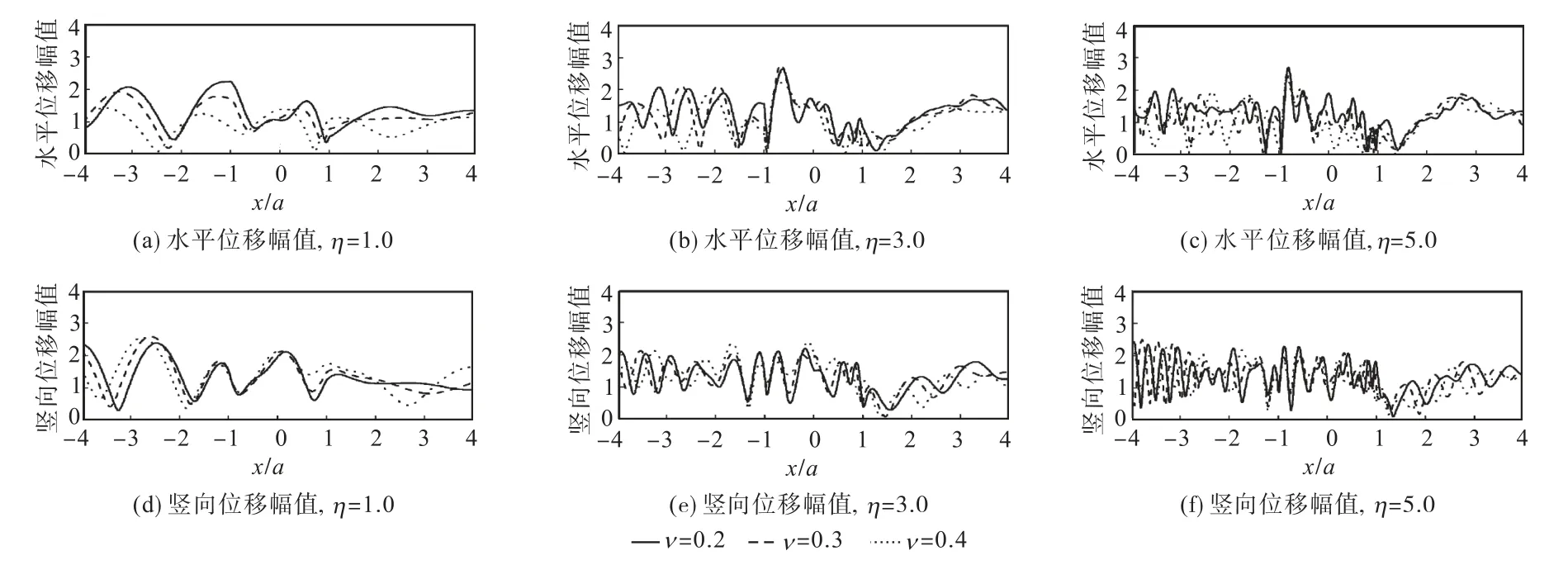
图7 泊松比对地表位移幅值的影响(透水情况, θ α1 =45°,n=0.3)Fig.7 Normalized surface displacement for different Poisson’s ratios(drained case, θ α1 =45°,n=0.3)

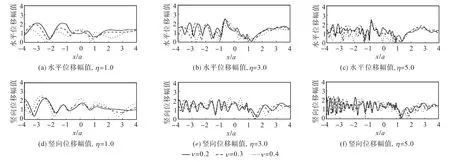
图8 泊松比对地表位移幅值的影响(不透水情况, θ α1 =45°,n=0.3)Fig.8 Normalized surface displacement for different Poisson’s ratios(undrained case, θ α1 =45°,n=0.3)

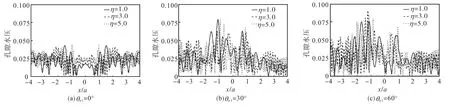
图9 地表孔隙水压(n=0.1，ν =0.25)Fig.9 Pore pressure at surface(n=0.1，ν =0.25)

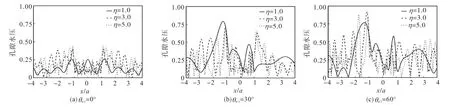
图10 地表孔隙水压(n=0.3, ν=0.25)Fig.10 Pore pressure at surface(n=0.3, ν=0.25)

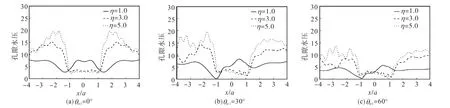
图11 地表孔隙水压(n=0.36, ν=0.25)Fig.11 Pore pressure at surface(n=0.36, ν=0.25)

3 结 论

(1)饱和情况(透水或不透水)与干土情况地表位移的差别很大，饱和情况与干土情况的地表位移出现相位漂移，饱和情况地表位移波长相对较大．

(2)当孔隙率较低时，边界渗透条件对地表位移幅值的影响很小，而当孔隙率较大时，边界渗透条件的影响则不可忽视：不透水情况下，水平和竖向地表位移幅值的峰值均相对较大．随着入射频率的升高，孔隙率的影响逐渐增大，而且不透水情况下孔隙率的影响相对较大．

(3)随着泊松比的增大，水平位移幅值逐渐减小，竖向位移幅值则逐渐增大．泊松比较小时，边界渗透条件对位移幅值的影响较大；泊松比较大时，边界渗透条件对位移幅值的影响则较小．随着入射频率的升高，泊松比的影响逐渐增大．

(4)当孔隙率较小时，孔隙水压幅值较小但空间变化比较剧烈，随着孔隙率的增大，孔隙水压逐渐增大但空间变化逐渐平缓．当孔隙率达到临界状态时，孔隙水压显著增大，这与 SV波入射情况完全不同．当入射频率较高时，孔隙水压幅值较大，且孔隙水压的空间变化比较复杂．

［1］ Trifunac M D. Scattering of plane SH wave by a semicylindrical canyon[J]. Int J Earthq Engng Struct Dyn，1973，1：267-281.

［2］ Cao H，Lee V W. Scattering and diffraction of plane P waves by circular cylindrical canyons with variable depth to width ratio [J]. Soil Dynamics and Earthquake Engineering，1990，9(3)：141-150.

［3］ Kawase H. Time-domain response of a semi-circular canyon for incident SV，P，and Rayleigh waves calculated by the discrete wavenumber boundary element method[J]. Bulletin of Seismological Society of America，1988，78：1415-1437.

［4］ Sanchez-Sesma F J，Campillo M. Diffraction of P，SV，and Rayleigh waves by topographic features：A boundary integral formulation [J]. Bulletin of Seismological Society of America，1991，81(6)：2234-2253.

［5］ Biot M A . Theory of propagation of elastic waves in a fluid-saturated porous solid(I)：Low frequency range [J].J Acoust Soc Am，1956，28：168-178.

［6］ Lin C H，Lee V W，Trifunac M D. The reflection of plane waves in a poroelastic half-space fluid saturated with inviscid fluid [J]. Soil Dynamics and Earthquake Engineering，2005，25：205-223.

［7］ 李伟华，赵成刚．圆弧形凹陷饱和土场地对平面 P波散射问题的解析解[J].地球物理学报，2003，46(4)：539-546.Li Weihua，Zhao Chenggang．An analytical solution for the diffraction of plane P-waves by circular cylindrical canyons in a fluid-saturated porous media half space[J].Chinese Journal of Geophysics，2003，46(4)：539-546(in Chinese).

［8］ Liang J，Ba Z，Lee V W. Diffraction of plane SV waves by a shallow circular-arc canyon in a saturated poroelastic half-space [J]. Soil Dynamics and Earthquake Engineering，2006，26：582-610.